Phong Model
-
물체를 Lighting하기 위해서는, 물체 표면으로 들어오는 빛과 카메라를 향해 나가는 빛 사이의 관계를
BRDF(bidirectional reflectance distribution function)으로 정의해야 한다. -
퐁 모델은 실시간 rendering을 위해서 이 BRDF를 극단적으로 단순화했다.
-
퐁 모델은 물체 표면에서 감지되는 색상을
디퓨즈(diffuse), 스페큘러(specular), 앰비언트(amvient) 반사와, 발산(emissive light)
네 가지 항목을 더해 처리한다. -
디퓨즈 및 스페큘러 항은 광원으로부터 물체 표면에 직접 들어오는 빛 즉 직접 조명을 다루는 반면,
앰비언트 항은 다른 물체가 반사하는 빛 즉 간접 조명을 다룬다.
발산광은 물체 스스로 빛을 발산하는 경우에 사용된다. -
퐁 모델:
diffuse +
specular +
ambient +
emissive light
Diffuse Term - 난반사
-
은 빛의 양을 결정, ( 이 음수가 되는 경우 0으로 처리)
은 반사되는 빛의 color 결정.
: 광원의 RGB 색상, : 물체의 diffuse 계수
-
Diffuse 표면이라 불리는 이상적인 표면으로 들어온 빛은
모든 방향을 따라 같은 방향으로 반사된다. ➡️ 이를 난반사라고 한다. -
카메라에 의해 감지되는 빛은 카메라의 시선에 무관하며,
오로지 물체 표면에 들어오는 빛의 양에 비례한다. -
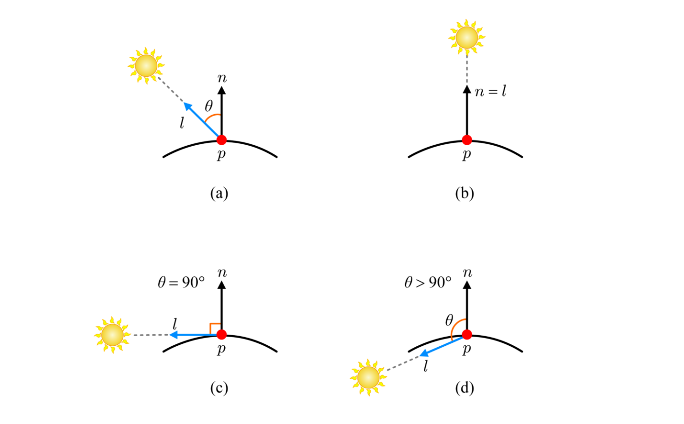
물체 표면의 점 의 normal 과
빛 벡터 ,
벡터 과 사이의 각도 인 입사각을 이용한다.

Specular Term - 정반사
: highlight가 감소되는 정도.
: 표면의 매끈함의 정도, 가 커질수록 highlight는 급격히 감소.
: 광원의 색상. 반사되는 정도 조절, : 물체의 specular 계수
(는 와 달리 회색조(gray-scale)로 표현되는데, 이는 물체 표면의 highlight가 광원의 색을 반영하도록 하기 위함.)
-
specular term은 물체 표면에 highlight를 만드는 데 사용됨.
-
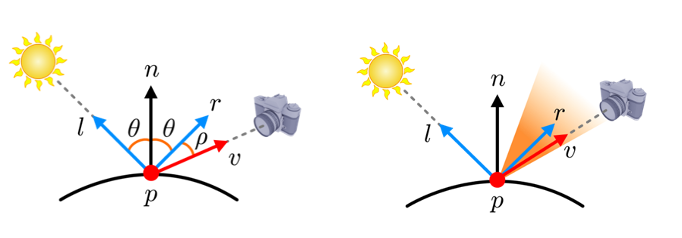
specular term 계산을 위해서 view vector와 reflection vector가 필요함.
-
highlight를 볼 수 있는 영역은 을 중심으로 한 원뿔 모양으로 묘사할 수 있다.
만약 가 원뿔 안에 놓이면, camera는 highlight를 볼 수 있다.
원뿔 속에서 highlight가 감소되는 정도는 다음과 같이 근사적으로 계산된다.

Ambient Term
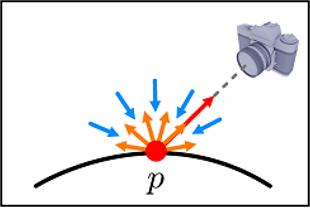
-
ambient 반사는 다음과 같이 간단하게 정의된다.
ambient light의 생상
object의 ambient 계수 -
ambient light: 공간 내 다양한 object로부터 반사된 빛.
간접 조명에 해당함. -
모든 방향을 따라 점에 들어온다.
따라서 에서 모든 방향을 따라 반사된다.
결국, 에 들어오는 ambient light의 양은 의 normal에 무관하고,
에서 반사되는 빛의 양은 camera 시선에 무관하다. -
ambient term 덕분에, 광원으로부터 비이 직접 닿지 않는 부분에도 lighting 효과를 줄 수 있다.

Emission light term
-
object 자신이 빛을 발산하는 경우에 사용된다.
-
퐁 모델은 발산광을 가진 물체를 광원으로 취급하지 않는다.
그래서 같은 공간의 다른 물체를 lighting 하는 데 기여하지 못한다.
이것은 퐁 모델의 한계 중 하나이다.
퐁 모델 정리

퐁 lighting을 위한 shader
-
한 점마다 하나의 fragment가 생성된다고 가정하자.
fragment shader는 각 점마다 퐁 모델 수식을 이용해 lighting을 수행할 것이다.
이를 위해서는 빛 벡터 , normal , 반사 벡터 , view vector 가 필요하다. -
은 fragment shader에게 uniform으로 제공되며,
fragment shader는 과 를 입력받는다.
또한, 은 을 이용해 계산한다. -
vertex shader
1) vertex normal 을 object space에서 world space로 변환한다.
그리고 rasterizer에게 넘겨준다.
왜냐하면, 광원이 world space에 있으므로, 빛 벡터 은 world space에서 정의되기 때문에,
퐁 모델 diffuse term에서 과 결합될 역시 world space vector여야 한다.
rasterizer는 이를 interpolation하여 각 fragment마다 world space normal 을 할당한다.
2) 각 vertex의 object space 좌표를 world space로 변환한 후,
이를 카메라(EYE)와 연결하여,
world space view vector 과 를 계산한다.
rasterizer는 이를 interpolation하여 각 fragment마다 world space view vector 을 할당한다. -
예시
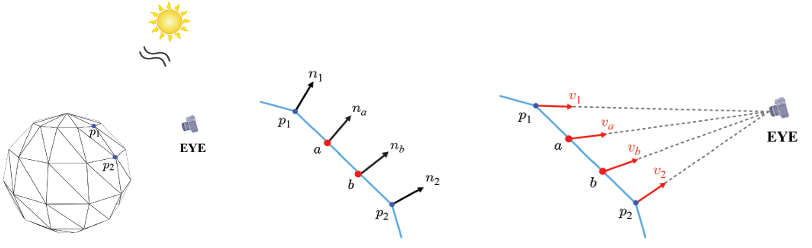
[normal vector]
구를 표현하는 mesh의 두 정점 과 를 보자.
과 각각의 world space normal 과 를 보여준다.
한편, 과 를 잇는 선분 상의 두 점 와 가 각각 fragment를 생성한다고 가정하자.
rasterizer는 과 를 interpolation하여, normal 와 를 계산한다.