-
두 개의 n 차원 벡터
a=(a1,a2,...,an)
b=(b1,b2,...,bn) 일 때,
a⋅b=∑t=1naibi=a1b1+a2b2+...+anbn
-
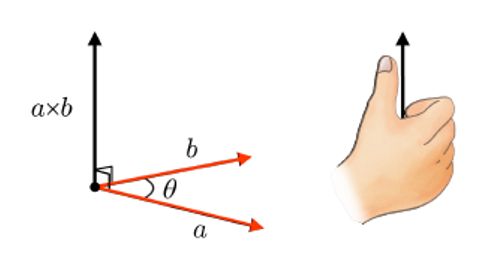
a⋅b=∣∣a∣∣ ∣∣b∣∣cosθ
-
오른손 법칙을 따름.
-
∣∣a×b∣∣=∣∣a∣∣ ∣∣b∣∣sinθ
-
a×b의 길이는 a와 b에 의해 만들어지는 평행사변형의 넓이와 같다.
-
두 벡터
a=(ax,ay,az)
b=(bx,by,bz) 일 때,
a×b=(aybz−azby,azbx−axbz,axby−aybx)
-
a×b=−(a×b)
-
두 개의 점 p0와 p1을 지나는 직선은 p0와, p0와 p1를 잇는 벡터 p1−p0를 사용해 매개변수 방정식(parametric equation)으로 정의됨.
p(t)=p0+t(p1−p0)
-
여기서 t는 [−∞,∞] 범위에 놓이는 매개변수(parameter)이다.
-
만약 t의 범위가 [0,∞]이라면, p0에서 시작해서 p1−p0 방향으로 무한하게 뻗어나가는 광선(ray)가 됨.
-
(1−t) 와 t를 각각 p0와 p1에 대한 가중치(weight)로 보면,
p(t)는 p0와 p1의 가중치 합(weight sum)이 된다.
t가 0일수록 p0에 가까워지고, t가 1일수록 p1에 가까워지게 된다.
-
특히, t의 범위가 [0,1]일 때, p(t)는 p0와 p1의 선형보간(linear interpolation)이라고 한다.
-
함수 p(t)는 2차원 공간에서는 (x(t),y(t)), 3차원 공간에서는 (x(t),y(t),z(t))가 된다.
p0와 p1의 3차원 좌표를 각각 (x0,y0,z0)와 (x1,y1,z1)이라고 할 때, 각 좌표값에 선형보간을 적용해 p(t)의 좌표를 얻는다.
p(t)=⎝⎜⎛x(t)y(t)z(t)⎠⎟⎞=⎝⎜⎛(1−t)x0+tx1(1−t)y0+ty1(1−t)z0+tz1⎠⎟⎞
-
만약, p0와 p1에 특정한 값이 저장되어 있다면, 그 값들도 선형보간될 수 있다.
예를 들어, p0에 c0라는 색상이 저장되어 있고 그 원소를 (R0,G0,B0)라 하자.
마찬가지로, p1에 c1이라는 색상이 저장되어 있고 그 원소를 (R1,G1,B1)라 하자.
RGB 원소 각각은 대개 [0, 255] 범위의 정수값, 혹은 [0, 1] 범위의 실수값을 가지는데,
선형보간된 색상 c(t)는 다음과 같이 정의된다.
c(t)=(1−t)c0+tc1=⎝⎜⎛(1−t)R0+tR1(1−t)G0+tG1(1−t)B0+tB1⎠⎟⎞