항해99-17기 1일차 TIL
드디어 본 과정 첫 날이다. 걱정 반 기대 반으로 시작한 첫 날,
심화트랙은 1주차부터 3주차까지 알고리즘 주차로 시작한다.
자료구조를 공부하며 알고리즘을 풀어 가는 방식으로 구성된 듯하다.
파이썬의 문법을 모르는 채로 시작한 알고리즘 문제 풀이라 아무래도 어려움이 있다.
사실 그보다 더 험난한 것은 실제로 어려운 문제가 섞여서 나왔다.
문법을 모르는 부분은, 틈틈이 시청하는 파이썬 강의와 그때그때 궁금한 부분을 검색하여 해결한다.
JS로 공부했던 것과 비슷한 자료형이나 구조, 메소드가 나오기도 하고
JS와는 다른 새로운 메소드나 자료형이나 그 활용 등이 있다.
알고리즘을 풀기 위해 고민하는 것도 재미있고 시간이 잘 가지만,
막혀서 풀지 못한 알고리즘의 해설을 찾는다거나 새로운 문법 같은 것을 알게 되는 것이 아주 재밌다.
알고리즘 문제 풀이에 익숙해지면서 메소드나 문법도 익숙해지고 원활히 쓸 수 있게 되면 좋겠다.
팀원들과의 과제 발표 등의 스터디도 좋다.
정말 해설보다 스스로의 생각으로 알고리즘에 접근하려는 모습이 보이면서 풀어내고,
코드는 물론 스터디에서 설명해주시는 부분도 이해와 공부가 된다.
첫날이라 그런지 긴장도 했고, 서론이 길어졌다. 아래는 본격적으로 오늘의 TIL이다.
1. 자료 구조
# 빅오 (Big-O)
빅오를 기억하기 전, 미리 기억하면 좋을 만한 게 '시간복잡도'이다.
'시간복잡도'란, 어떤 알고리즘을 수행하는 데에 걸리는 시간을 설명하는 계산복잡도라고 한다.
보통 계수를 제외한 최고차항만을 표기한다. (ex. 4n^2 + 3n + 4의 시간복잡도는 n^2라고 할 수 있다.)
빅오(O)는, 점근적 실행 시간을 표기할 때, 가장 많이 사용하는 수학적 표기법이라고 한다.
이는 시간복잡도의 상한선을 의미한다.
예를 들어, O(n^2) 라는 식의 빅오가 있다면,
n^2의 시간복잡도나 n의 시간복잡도, log n의 시간복잡도 등은 문제가 안 된다.
다만 n^3나 2^n과 같이, n^2보다 큰 시간복잡도를 가지게 되면 상한선을 넘는 것이 된다.
시간복잡도의 제한을 둔 알고리즘 문제를 풀 때 빅오를 넘기는 시간복잡도를 가지면
알고리즘 자체는 맞더라도 실행 시간이 초과하여 실패할 수 있다.
빅오를 가장 많이 사용하지만, 반대로 최선의 개념인 빅오메가와 평균의 개념인 빅세타도 있다.
또, 분할 상환 분석이라는 개념도 빅오와 더불어 함수의 동작을 수행할 때 중요한 개념이라고 한다.
이는 최악의 경우를 여러 번에 걸쳐 골고루 나눠 주는 형태로, 동적 배열 등에서 효율적으로 쓸 수 있다고 한다.
이 개념은 나중에 더 알아 보면 좋을 것 같다.
일부 알고리즘은 병렬화가 가능한데, 딥러닝이 그 예이다.
이 경우, 속도는 느리지만 코어 수가 많은 GPU를 활용해 연산을 동시에 수행한다.
짐을 많이 싣진 못하지만 속도가 빠른 비행기가 CPU라고 하면,
짐을 많이 실을 수 있지만 속력은 느린 화물선이 GPU라고 할 수 있다.
# Python의 자료형
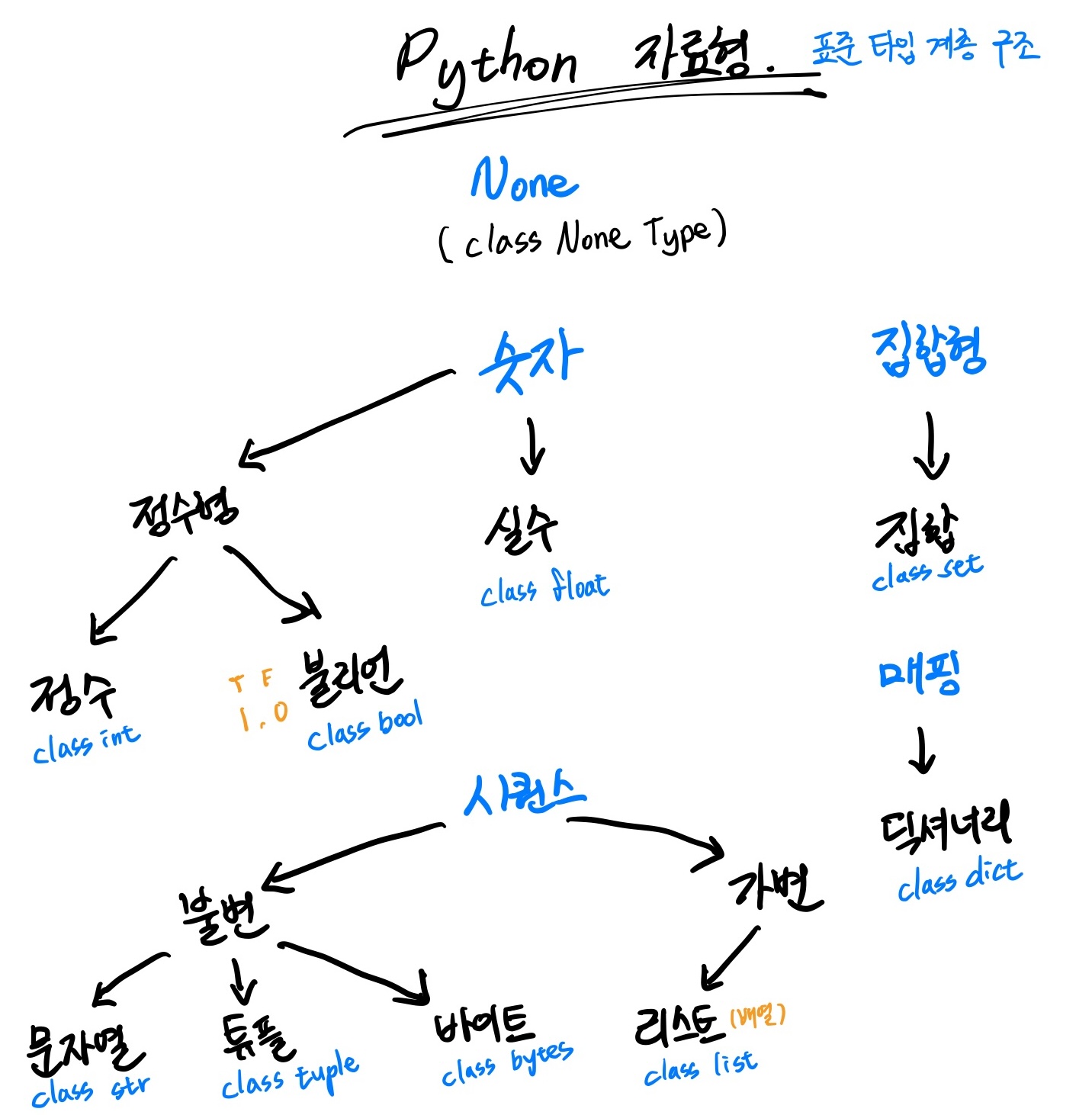
대략 표준 타입이다.
# 그리고 원시 타입이나 객체 등이 있다 - 파이썬은 모든 것이 객체이다. (불변/가변)
원시 타입의 경우, 메모리 할당 등을 효율적으로 설계하여 실행 시간을 줄이는 부분에 있어 유리하다.
파이썬은 효율보다는 인간 친화적인 언어이며, 라이브러리나 모듈이 다양하며
모두 객체로 되어 있어(메모리 여유가 있어) 다양한 작업을 하거나 보다 쉽고 편하게 이용할 수 있다.
오늘 공부한 자료 구조는 이 정도이다.
쓰다 보니 길어져서 스터디 발표를 진행한 과제는 새 글로 작성하려 한다.