Linear Regression - Overfitting & Regularization

Overfitting and Regularization

Overcoming Overfitting

계속 iteration 돌 때의 문제점은 Overfitting이 일어나는 것이다.
Overfitting은 Trained data와 Test data가 있을 때, 너무 Trained data에만 맞고 testdata에는 안 맞는 경우이다.

즉, 학습데이터에 치중되어서 최적화되어 새로운 데즉이터의 예측이 어려워진다.

Occam's razor

보다 적은 수의 논리로 설명이 가능한 경우, 많은 수의 논리를 세우지 말라

• 이를 머신러닝에 적용한다면.
  적은 수의 파라미터로도 예측이 가능하다면,
  많은 파라미터를 만들지 마라

Bias - Variance tradeoff

파라미터 수 자체는 Bias와 Variance는 서로 trade off라는 것이 있다.

High bias
원래 모델에서 많이 떨어진 잘못된 데이터로만 계속 학습을 했을 때, bias가 높다라고도 하며, underfitting이라고도 한다.
→ 잘못된 Weight만 Update

High variance
모든 데이터에 민감하게 학습이 되어서 데이터가 떨어지는 것이다.
데이터의 차이가 너무 큰 경우라고 말하며, overfitting이라고도 한다.
→ 모든 Weight가 Update

Overcoming Overfitting

• 더 많은 데이터를 활용한다.
  • 'Gan' : fake 데이터를 만드는 것이다.
  • 페이크 사진 등을 만들어서 학습 능력을 높이는 방법이다.
• Feature의 개수를 줄인다.
• 적절히 Parameter를 선정한다.
  • 적절한 hyperparameter를 찾아내는 방법이 Regularization이다.
• Regularization

Regularization

• cost function을 최소화시킬 때 아래의 수식과 같이 weight 값에 패널티를 줄 수 있다.
  $J(w_0, w_1) = \frac{1}{2m} \sum_{i=1}^{m} \left( w_1 x^{(i)} + w_0 - y^{(i)} \right)^2$
• $\theta$를 한 단위 늘리면 cost 값은 1000까지 늘어난다.
• 이를 패널티를 준다고 한다.
• 이 cost function을 줄이는 것이 일반적인 목표이기 때문에, 알고리즘에서 $\theta$ 값이 많이 늘어나지 않게끔 만드는 것이다.

L2 regularization

• norm (노름) : 벡터의 길이 혹은 크기를 측정하는 방법
• L2는 Euclidean distance라고 한다.
  이는 원점에서 벡터 좌표까지의 거리를 피타고라스 정리를 사용하여 제곱 후 합을 구해준 후, 루트를 씌워 거리를 구해주는 방법을 말한다.

L2 Regularization 식은 아래와 같다.

• 첫 번째 항은 기존의 평균 제곱 오차(MSE) 기반의 Cost function을 의미한다.
• 두 번째 항은 L2 정규화 항으로,
  • $\lambda$ 는 정규화 계수이며,
  • $\theta_j^2$ 는 각 파라미터의 제곱 (L2 norm)을 의미한다.

이를 미분했을 때 절편값에 대한 패널티를 구하지는 않는다.
절편값을 같이 줄게 되면, y값도 같이 줄어들기 때문에 패널티를 구하지 않는다.

수식을 자세하게 조금 더 풀면 아래와 같은 식이 나온다.

원래의 정규화 포함 Gradient Descent 식은 다음과 같다.

첫 번째 항은 기존의 경사 하강법의 파생 항이고,
두 번째 항은 $\frac{\lambda}{m} \theta_j$는 정규화 항으로 L2 penalty이다.

오버피팅을 방지하기 위해 파라미터 값을 제어하는 역할을 한다.

위의 식을 정리한 형태는 아래와 같다.

기존 파라미터 $\theta_j$를 $(1 - \alpha \cdot \frac{\lambda}{m})$ 만큼 줄이고
손실 함수의 gradient를 기반으로 학습 방향을 반영한다.

L1 regularizatioin

L1 regularization은 L2랑 달리 절댓값을 가진다.
이 절대값으로 L2보다는 패널티를 적게 주는 방식이다.

기존 Cost function L1(norm) penalty term을 추가한다.
L1은 manhattan distance 방식을 따르며, 원점에서 벡터 좌표까지의 거리를 구하는 방식이다.

w의 값을 제한한다.
L2는 제곱으로 제한을 하게 되며,
L1은 절대값으로 제한을 한다.

L1 vs. L2

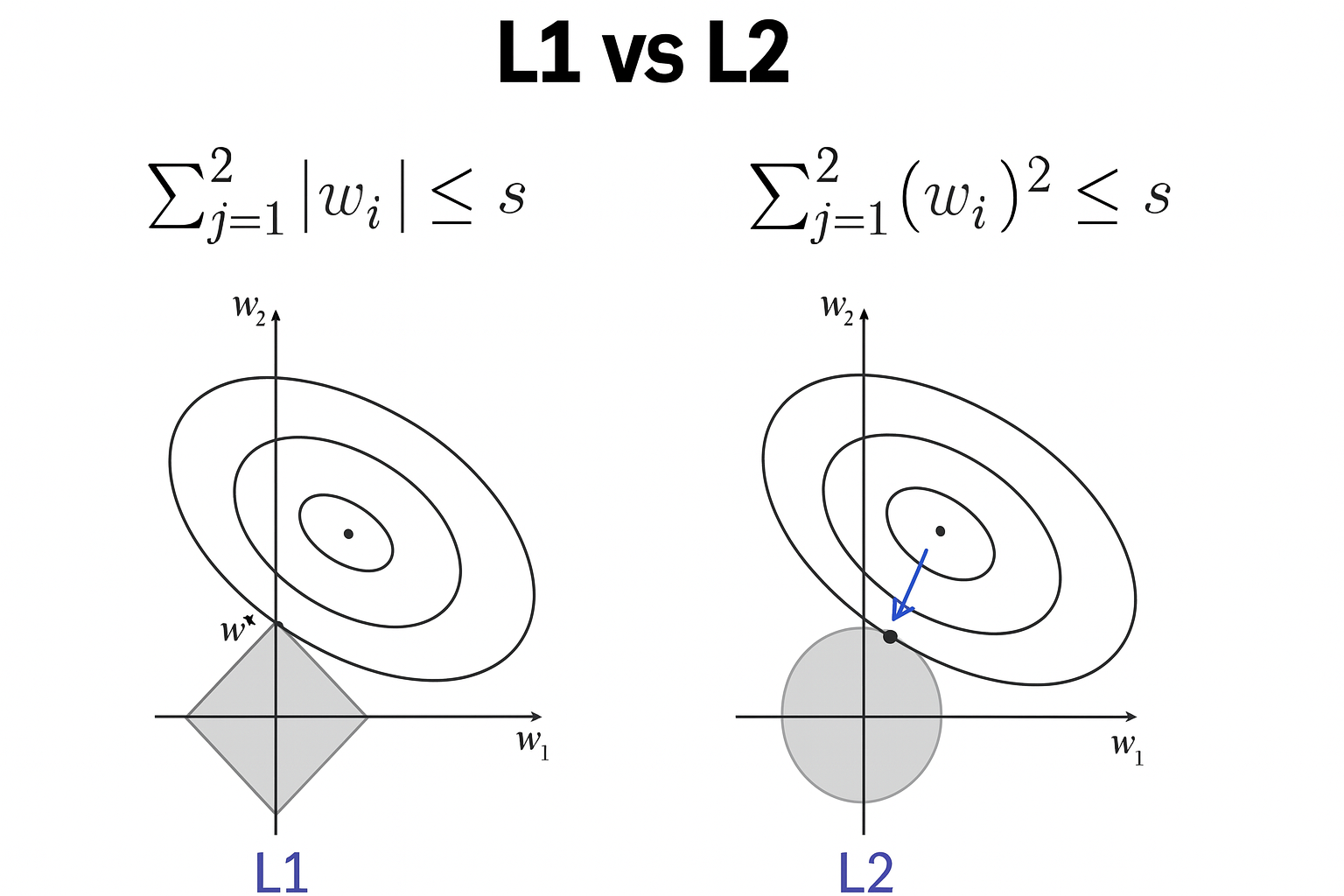
• L2 의 경우는 타원과 한 점이 반드시 한 점에서만 만나게 된다.
  • 그래서 w값이 한 개의 값이 나온다.
• L1 같은 경우 절대값이라 사각형 모양이 나온다.
  • 그래서 여러 점이 만나게 될 수도 있다.

차이점

L1	L2
Unstable solution	Stable solution
Always on solution	Only one solution
Sparse solution	Non-sparse solution
Feature selection

L1은 weight값이 0으로 나오게 될 수도 있다.

REFERENCE

• https://www.boostcourse.org/ai222/joinLectures/27857?isDesc=false