Stochastic Gradient Descent

연·2025년 7월 26일

just공부

목록 보기

32/47

Goal

Stochastic Gradient Descent 알고리즘

Gradient Descent와의 차이점

각 알고리즘의 장단점

hyper-parameter(epoch, batch size)

Gradient descent

그래프 상에서 임의의 한 점을 잡아서 기울기 방향으로 이동해 가는 최적화 알고리즘이다.

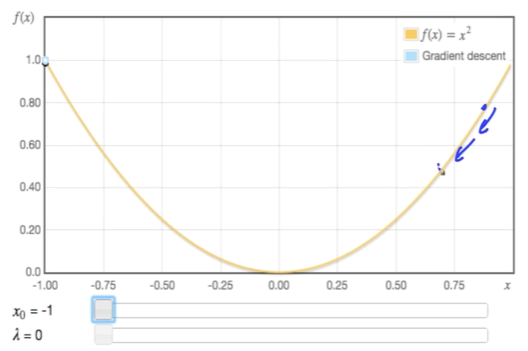
Batch Gradient Descent 기준

실제로는 한 점이 아니라, 전체 점이다.
- 전체 데이터를 기반으로 한 번에 가중치를 업데이트
한 번에 여러 개의 점의 평균값을 업데이트하게 된다.

Full-batch Gradient descent

우리가 알고리즘에서 사용할 때는 Full-batch Gradient descent 라고 부르는 개념이다.

미분값을 구할 때 전체 값을 다 구해준다.

\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1) \\ \frac{\partial J}{\partial w_n} = \frac{1}{m} \sum_{i=1}^{m} \left( \mathbf{w}^T \mathbf{x}^{(i)} - y^{(i)} \right) \cdot x_n

미분값을 구할 때, 전체 데이터인 N개 만큼의 값을 구해주는 것이 핵심이다.

업데이트 감소 → 계산상 효율적(속도) 가능
안정적인 Cost 함수 수렴
지역 최적화 가능
메모리 문제 (ex - 30억개의 데이터를 한번에?)
대규모 dataset → 모델/파라미터 업데이트가 느려진다.

위와 같은 속도가 느려진다는 점이 있어서 Stochastic gradient descent 를 사용한다.

Stochastic gradient descent

확률적인 경사하강법이다.
한 점씩 돌아가면서 gradient 를 구하는 것이다.

원래 의미는 dataset에서 random하게 training sample을 뽑은 후 학습할 때 사용한다.
Data를 넣기 전에 Shuffle

procedure SGD
	shuffle(X)							▷ Randomly shuffle data
 	for i in number of X do
    	θ_j := θ_j - α (ŷ⁽ⁱ⁾ - y⁽ⁱ⁾) xⱼ⁽ⁱ⁾     ▷ Only one example
    end for
end procedure

빈번한 업데이트 모델 성능 및 개선 속도를 확인해볼 수 있다.
일부 문제에 대해 빨리 수렴한다.
지역 최적화 회피
대용량 데이터시 시간이 오래걸린다.
더이상 cost가 줄어들지 않는 시점의 발견이 어렵다.

위와 같은 문제점이 있기 때문에 사용하는 것이 Mini-batch (stochastic) gradient descent 이다.

Mini-batch (stochastic) gradient descent

데이터를 일부 사용하는 것이다.

한번의 일정량의 데이터를 랜덤하게 뽑아서 학습시킨다.
SGD와 Batch GD를 혼합한 기법이다.
가장 일반적으로 많이 쓰이는 기법이다.
모든 Optimize Algorithm이 이 방법이다.

Epoch & Batch-size

전체 데이터가 Training 데이터에 들어갈 때 카운팅한다.
Full-batch를 n번 실행하면 n epoch
- 1 epoch이라고 하면, Full-batch가 한 번 돈 것이다.
- 1,000번 iteration 한다고 하면, 1000 epoch 이라는 뜻이다.
Batch-size : 한 번에 학습되는 데이터의 개수이다.
- 128 x 8일 경우, 128 batch-size가 되는 것이다.
- 128개가 8번 돌아가면, 1 epoch이 되는 것이다.
총 5,120개의 Training data에 512 batch-size면 몇 번 학습을 해야 1 epoch이 되는가?
- 10번겠지..

Mini-batch SGD

procedure MINI-BATCH SGD
	shuffle(X)			▷ Randomly shuffle data
    BS <- BATCH SIZE
    NB <- Number of Batches
    NB <- len(X)//BS
    for i in NB do
    	θ_j := θ_j - α ∑_{k = i×BS}^{(i+1)×BS} (ŷ⁽ᵏ⁾ - y⁽ᵏ⁾) xⱼ⁽ᵏ⁾    ▷ Batch-sized examples

1 epoch인 BATCH SIZE가 100이라고 가정한다면
Number of Batches는 10이라고 하자.

$k=i×BS$ 에 x[0 : 10], x[10 : 20] 이런 식으로, x에서 0부터 10까지 뽑아서 넣어주고, 10부터 20까지 학습시키는 것이다.

i는 Number of Batches

for epoch in range(epoches):		# 전체 Epoch이 iteration 되는 횟수
	X_copy = np.array(X)
    if is_SGD:			# SGD 여부 -> SGD일 경우 shuffle
    	np,random.shuffle(X_copy)
    batch = len(X_copy) // BATCH_SIZE		# 한번에 처리하는 BATCH_SIZE
    for batch_count in range(batch):
    	X_batch = np.copy(
        	X_copy(batch_count*BATCH)SIZE : (batch_count+1)*BATCH_SIZE])
        # Do weight Update				BATCH_SIZE 크기만큼 X_batch 생성
    print("Number of epoch : %d" % epoch)

Convergence process

gd_lr = linear_model.LinearRegressionGD(eta0=0.001, epochs=10000, batch_size=1, shuffle=False)
bgd_lr = linear_model.LinearRegressionGD(eta0=0.001, epochs=10000, batch_size=len(X), shuffle=False)
sgd_lr = linear_model.LinearRegressionGD(eta0=0.001, epochs=10000, batch_size=1, shuffle=True)
msgd_lr = linear_model.LinearRegressionGD(eta0=0.001, epochs=10000, batch_size=100, shuffle=True)