Python for ML

연·2025년 7월 22일

just공부

목록 보기
29/41

Machine Learning Process

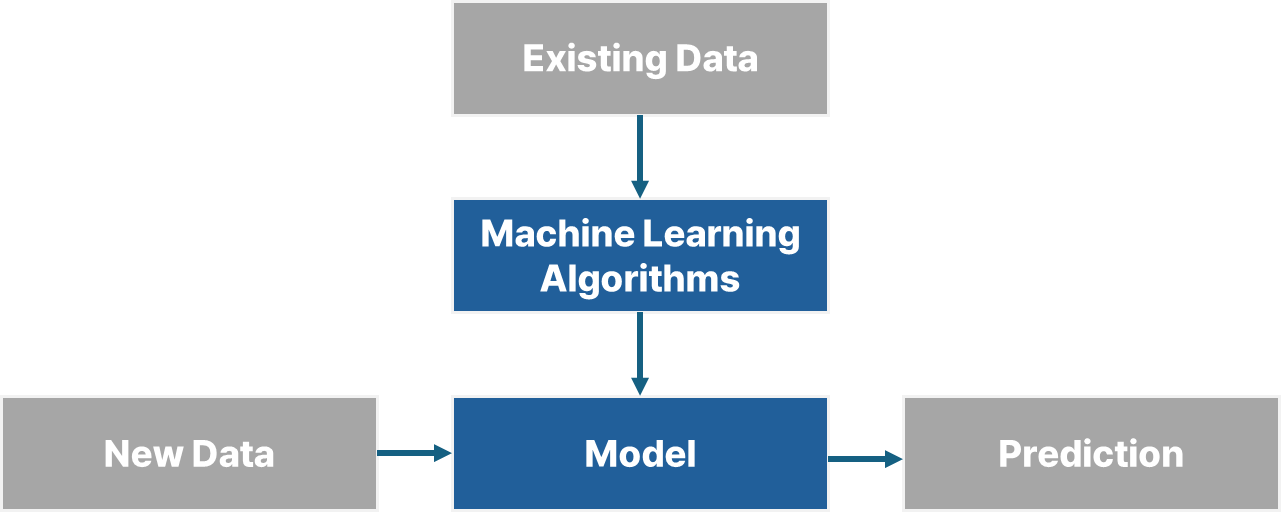
Key concepts

  • Model : 예측을 위한 수학 공식, 함수
    • 1차 방정식, 확률분포, condition rule
  • Algorithms : 어떠한 문제를 풀기 위한 과정
    • Model을 생성하기 위한 (훈련) 과정

모델을 학습할 때 영향을 주는 것들

  • y = ax + b
    • y - 주어진 Y값: 종속변수
    • a, b - 알고리즘을 통해 최적값을 찾음
    • x - 주어진 X값: 독립변수

y에 대해 영향을 줄 수 있는 x는 여러 개가 존재할 수 있다.
X변수의 실제 데이터는 특징(feature)을 나타낸다.

y=β1x1+β2x2+⋯+β13x13+β0⋅1y = \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_{13} x_{13} + \beta_0\cdot 1

feature vector

  • x\mathbf{x} : 특징(feature) 벡터
  • w\mathbf{w} : 가중치(weight) 벡터
  • wTx\mathbf{w}^T \mathbf{x} : 가중치와 특징 벡터의 내적 -> 예측값 yy
  • x0=1\mathbf{x}_0=1 일 경우, w0\mathbf{w}_0 는 편향(bias) 항으로 사용된다.
y=w1x1+w2x2+⋯+w13x13+w0x0=∑i=013wixi=wTxy = w_1 x_1 + w_2 x_2 + \cdots + w_{13} x_{13} + w_0 x_0 = \sum_{i=0}^{13} w_i x_i = \mathbf{w}^T \mathbf{x}
  • 선형대수의 표기법
    w\mathbf{w}와 x\mathbf{x} 를 list 형태의 값으로 표현하게 되면, y의 값을 구할 수 있게 된다.

Representing a model

벡터를 Array로 표현하기

for each i∑j=013wjxj(i)=X⋅w,x0=1\text{for each } i \quad \sum_{j=0}^{13} w_j x_j^{(i)} = \mathbf{X} \cdot \mathbf{w}, \quad x_0 = 1
  • ii : 데이터 Sample
  • j=0j=0 : Weight number
  • X\mathbf{X} : Data table

REFERENCE

profile
연
Whatever I want | Interested in DFIR, Security, Infra, Cloud
이전 포스트

Linear Algebra - Categorization

다음 포스트

Linear Regression

0개의 댓글