Module #4: Functions

1. Basic of Function

함수(function) : A, B가 집합일 때, A로부터 B로의 함수 f는 A의 원소 각각에 B의 원소를 단 하나만 대응 시킨 것이다.

• 함수에 대한 표현들
  
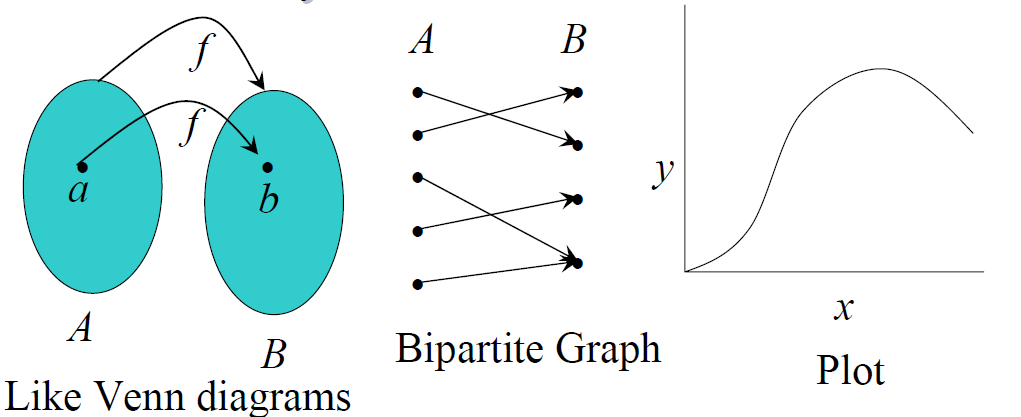
• 명제 : 상황이라는 정의역에서 {T, F}라는 공역으로 가는 함수
• bit String의 길이 : 숫자 {1, ..., n} 으로부터 bit {0,1}로 향하는 함수
• 집합 : 원소라는 정의역에서 존재하는지 여부인 {T, F}라는 공dur으로 가는 함수
• 집합 기호 : 집합으로부터 집합으로 가는 함수
  • ∩(({1,3},{3,4})) = {3}

Notations

• YX = f : X → Y 를 만족하는 모든 가능한 함수 F들의 집합

  • |F| = |Y||X|

• F ≡ 0, T ≡ 1, 2 ≡ {0, 1} = {F, T}

  f : A → B / f(a) = b (where a ∈ A & b ∈ B)
  A는 f의 정의역(domain)
  B는 f의 공역(codomain)
  B에서 f의 상(image)의 집합 치역(range)
  b는 f의 상(image)
  a는 f의 원상(pre-image)

• 상인 b는 일반적으로 1개 이상의 원상을 가진다

• 치역은 공역보다 작거나 같다

• 함수의 그래프 : f가 A→B인 함수일때, {(a, b) | a∈A 이고, f(a) = b, b∈B}인 순서쌍의 집합

  • 그림으로 표현할 수 있다.

Operator

• Operator : n개의 쌍에 대한 함수
  • Unary Operator : 인자가 1개 (ex. ~)
  • Binary Operator : 인자가 2개 (ex. ∪,∩)
• plus( + ) : 함수 합
  • (f + g)a = f(a) + g(a)
• times( × ) : 함수 곱
  • (f × g)a = f(a) × g(a)
• compose( $\circ$ ) : 함수 합성
  • (f $\circ$ g)a = f(g(a))
  • 교환 법칙이 성립하지 않는다.

---

2. Special Functions

One-to-One Function(1-1)

• 단사함수 : f의 정의역에 속한 모든 a와 b에 있어서 f(a) = f(b) 이면 반드시 a = b인 함수. (일대일 함수)
  
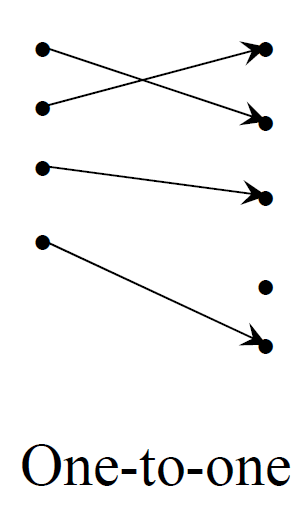
• 1개의 치역 원소에 1개의 정의역 원소만 대응
• Strictly increasing(단조 증가 함수) : 정의역 안의 임의의 원소 x, y가 x<y이면 반드시 f(x) < f(y)인 함수
• Strictly decreasing(단조 감소 함수) : 정의역 안의 임의의 원소 x, y가 x<y이면 반드시 f(x) > f(y)인 함수
  • f 가 단조 증가 or 단조 감소 함수이면 f는 단사 함수이다 (역은 성립 X)

Onto Function

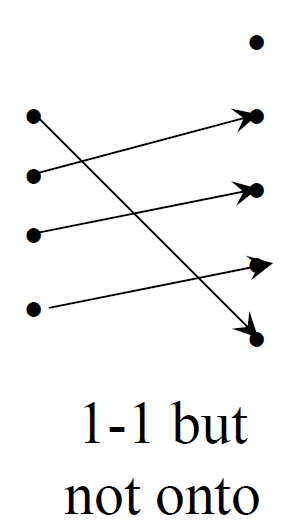
• 전사 함수 : 공역과 치역이 같은 함수
• 전사 함수 & 단사 함수 일수 있고, 한쪽만 만족할 수도 있다.
  
  

Bijections

• 전단사함수 : 전사함수이면서 동시에 단사함수인 함수. (일대일 대응)
  
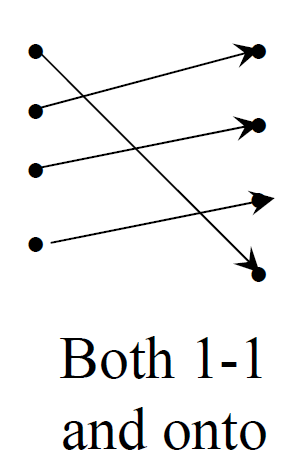
• f가 전단사함수일때, f의 역함수 f-1 : B → A 가 정의될 수 있다.
  • f-1 $\circ$ f = I(identity function)

Identity Function

• 항등 함수 : I : A → A , 입력과 출력이 같은 함수
• 항등함수는 전단사함수이다.
  

Floor & Ceiling Function

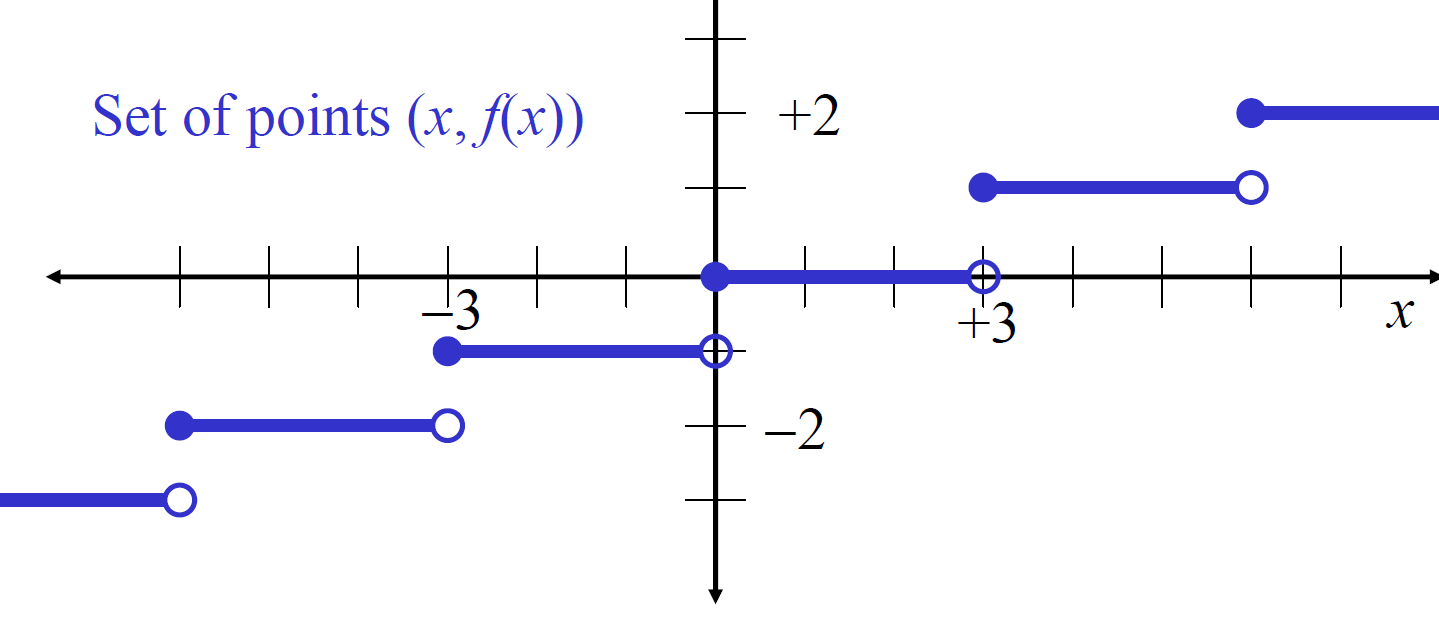
• Floor Function $\lfloor x \rfloor$ : 실수 x에 대해 x와 같거나 작은 수 중 가장 가까운 정수를 대응하는 함수.

• Ceiling Function $\lceil x \rceil$ : 실수 x에 대해 x와 같거나 큰 수중 가장 가까운 정수를 대응하는 함수.
  

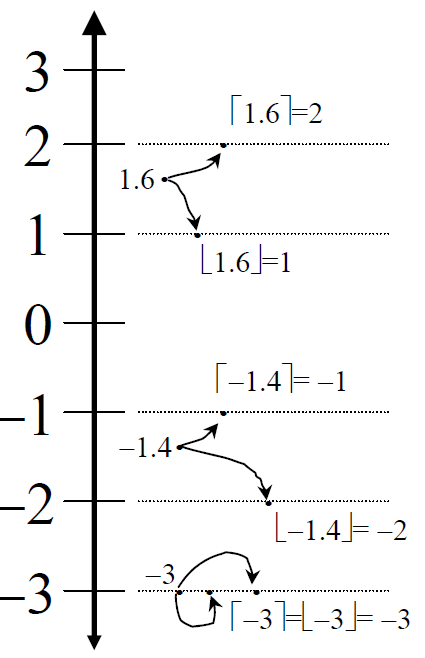
• if $x ∈ Z$, $\lfloor x \rfloor$ = $\lceil x \rceil$ = $x$

• ex) $\lfloor {x\over3} \rfloor$
  

---

3. Cardinality & Infinite Sets

• Define Cardinality for infinite set

• Cardinality : 1개의 relation(관계)에 포함되어 있는 tuple의 수

  두 집합 A와 B가 동일한 Cardinality를 가진다.(|A| = |B|)
  $\Longleftrightarrow$
  A 로부터 B로 향하는 전단사함수가 있다.

• 무한 집합일지라도 셀 수 있는 집합이 존재한다

  • 집합이 유한 or |S| = |N| 할 때
  • ex) N(자연수 집합), Z(정수 집합), 자연수의 순서쌍(n, m)

• 셀 수 없는 집합.

  • 집합이 무한 or |S| > |N|
  • ex) R(실수), C(복소수),
  • [0, 1) = {r ∈ R| 0 $\leq$ r $<$ 1|}

• Diagonalization 대각선 논법 : 실수의 집합은 셀 수 없다
  

• Transfinite Numbers

  • 무한집합 S가 셀 수 있을 경우 S의 크기를 $\aleph_0$ 라고 표기.
  • |N| = $\aleph_0$
    • 가장 작은 transfinite cardinal number(무한기수)
  • |R| = $\aleph_1$
    • second transfinite cardinal