Module #5: Algorithms

1. Property of Algorithms

알고리즘 : 계산을 하거나, 문제를 풀기 위한 정확한 명령의 유한한 서열

• 프로그램은 알고리즘을 구현한다.

Properties

• Input : 특정한 집합으로부터의 입력값
• Output : 입력한 값에 대한 출력값
• Definiteness : 알고리즘의 단계는 명확히 정의되어야 함
• Correctness : 어떠한 입력값에 대해서도 항상 정답을 구해야 함
• Finiteness : 유한한 횟수의 단계를 거쳐 답을 도출해야 함
• Effectiveness : 정확하고 유한한 시간 내에 수행해야 함
• Generality : 조건을 만족하는 모든 입력에 대해 적용 가능해야 함
• Efficiency : 최소한의 시간 & 공간을 사용 해야 함

Pseudocode

• 의사 코드, 알고리즘을 표현하는 방법

procedure 이름(인자: 타입)

ex) procedure maximum(L: list of integers)

변수 := 표현

• 의사 코드에선 정형화 되지 않은 표현도 허용된다.
  v := 3x + 7
  x := the largest integer in the list L
  swap x and y
  → 실제 프로그래밍 언어에선 사용 불가

begin
statements
end

if condition
then statement
→ 프로그래밍 언어의 if

while condition
statement
→ 프로그래밍 언어의 while

for var := initial to final
statement
→ 프로그래밍 언어의 for

{comment}
→ 주석, 설명을 덧붙이기 위해 사용

• example

  procedure max($a_1, a_2, ...,a_n$ : intergers)
     max := $a_1$      {largest element so far}
     for i := 2 to n      {go thru rest of elems}
          if max < $a_i$ then max := $a_i$      {found bigger?}
      {이 지점에서 max는 list의 원소 중 가장 큰 정수와 같다}
     return max {max is the largest element}

• example

  procedure sum($a_1, a_2, ...,a_n$ : intergers)
      s := 0      {sum of elems so far}
      for i := 1 to n      {go thru all elems}
          s := s + ai      {add current item}
      {이 지점에서 s는 모든 list 안의 값의 합}
     return s

2. Algorithms for Searching and Sorting

Search Algorithm

Linear Search

• 선형 탐색 : 차례대로 x를 다음 원소와 비교하며 일치하는지 확인하는 알고리즘

  procedure linear search(x : integer, $a_1, a_2, ..., a_n$: distinct integers)
     i := 1
     while (i ≤ n and x ≠ $a_i$)
          i := i+1
     if i ≤ n then location := i
     else location := i
     return location      {location is the subscript of the term that equal x, or is 0 if x is not found}

→ 시간 복잡도 : O(n)

Binary Search

• 이진 탐색 : 리스트 중간 원소 조사, 두 구간으로 나눠 어느 쪽에 있는지 판단하고 범위를 줄이는 알고리즘

  procedure binary search(x : integer, $a_1, a_2, ..., a_n$ : increasing integers)
     i := 1     {i is left endpoint of search interval}
     j := n     {j is right endpoint of search interval}
     while i < j
          m := $\lfloor(i+j)/2\rfloor$
          if $x > a_m$ then i := m + 1
          else j := m
     if x = $a_i$ then location := i
     else location := 0
     return location     {location is the subscript of the term $a_i$ equal to x, or 0 if x is not found

→ 시간 복잡도 : O(log n)

Sort Algorithm

Bubble Sort

• 버블 정렬 : 인접한 원소를 차례대로 비교, 순서가 잘못되어 있으면 서로 교환해 정렬하는 알고리즘

  procedure bubble sort($a_1, ..., a_n$ : real numbers with n ≥ 2)
     for i := 1 to n-1
          for j := 1 to n-i
              if $a_j > a_{j+1}$ then interchange $a_j$ and $a_{j+1}$
  {$a_1, ..., a_n$ is in increasing order}

→ 시간 복잡도 : O(n2

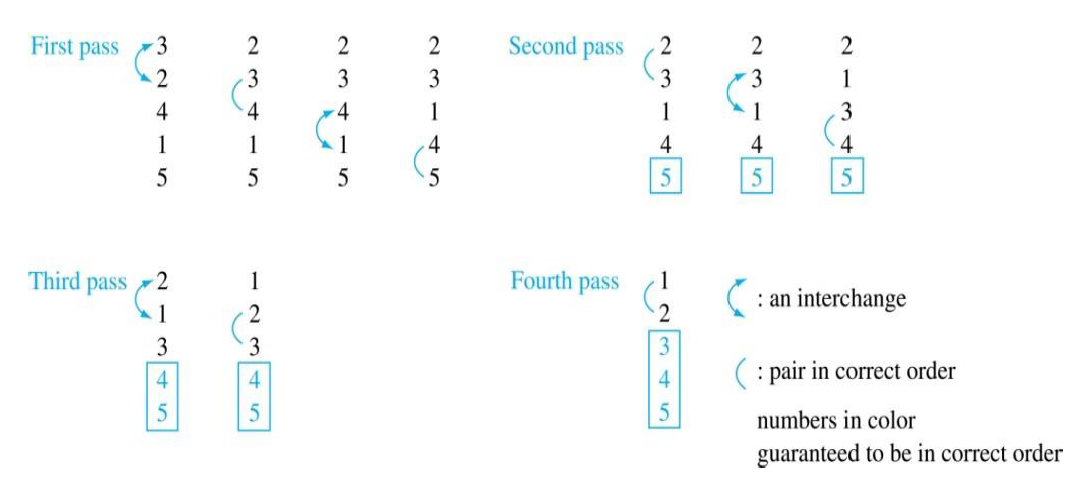
Insertion Sort

• 삽입 정렬 : - 두 번째 원소 부터 시작, 첫 원소와 비교해 앞/뒤 정해, 점점 뒤로가고, 앞쪽에서 정렬이 되는 알고리즘

  procedure insertion sort($a_1, a_2,...,a_n$: real numbers with n ≥ 2)
     for j := 2 to n
          i := 1
          while $a_j > a_i$
              i := i + 1
          m := $a_j$
          for k := 0 to j - i - 1
              $a_{j-k} := a_{j-k-1}$
          $a_i$ := m
  {$a_1, ..., a_n$ is in increasing order}

→ 시간 복잡도 : O(n2

3. Greedy Algorithms

욕심쟁이 알고리즘(greedy algorithm) : 각 단계마다 가장 좋은 선택을 하는 알고리즘

• 계산원 알고리즘 : 동전으로 거스름돈을 주는 방법을 계산하는 알고리즘

  procedure change($c_1, c_2, ..., c_n$: values of denominations of coins, where $c_1 > c_2 > ... >c_r$, n : a positive integer
     for i := 1 to r
          $d_i$ := 0 {$d_i$ counts the coins of denomination $c_i$ used}
          while n ≥ $c_i$
              $d_i$ := $d_i$ + 1 {andd a coin of denomination $c_i$
              n := n - $c_i$
  {$d_i$ is the number of coins of denomination $c_i$ in the change for i = 1, 2, …, r}

• greedy 알고리즘이 모든 알고리즘에 대한 답인 것은 아니다.

4. Halting Problem

• Halting Problem : 주어진 프로그램과 그 입력값에 대해 프고르갬이 유한한 시간 안에 종료될지, 아니면 무한 루프에 빠져 종료되지 않을지 판별하는 알고리즘은 존재하지 않는다.

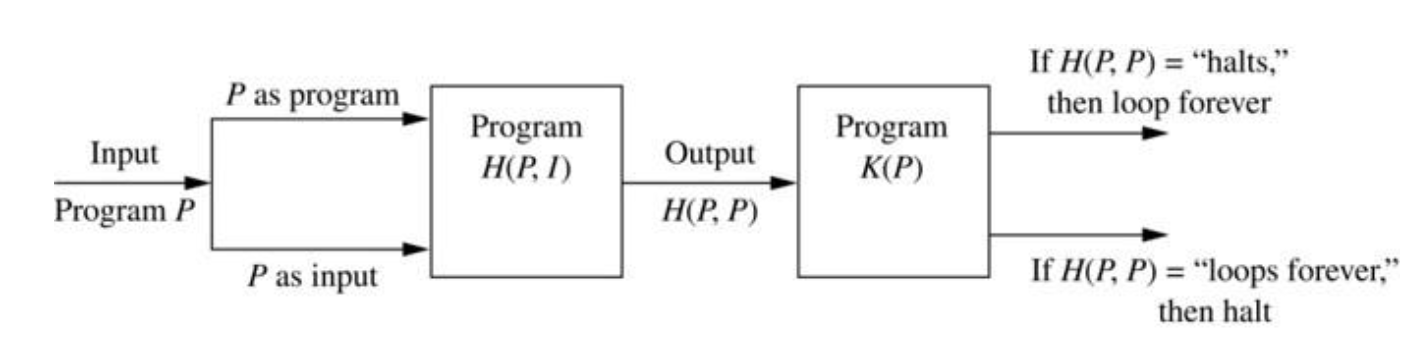
1. 입력으로 프로그램 P와 그 프로그램의 입력값 I를 받는 절차 H(P, I)가 있다고 가정.
2. H는 프로그램 P가 입력 I로 실행되었을 때, P가 멈출지 멈추지 않을지 판정하는 절차.

→ 해결할 수 없다는 것 증명
1. 가정 : 만약 H(P, I)라는 절차가 존재한다고 가정
2. 만약 프로그램이 멈추면 "halt", 멈추지 않으면 "loops forever" 출력
3. 프로그램 K(P) 정의

• 만약 H(P, P) 가 "loops forever" 출력할 시 K(P)는 멈춤.
• 만약 H(P, P) 가 "halt" 출력할 시 K(P)는 무한 루프.

4. K(K)를 호출한다면

• K(K)가 "loops forever" 라면 K(K)는 멈춘다 → 모순

• K(K)가 "halt" 라면 K(K)는 무한 루프에 빠진다 → 모순

• 따라서, Halting 문제를 해결할 수 있는 일반적인 알고리즘은 존재하지 않는다.