통계 라이브세션 1회차
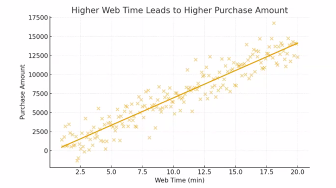
상관관계가 있다고 해서 인과관계가 있는건 아니다.
🔥가장 중요한 2가지🔥
1) AB테스트
2) X에 영향을 주는건 무엇일까?(인과관계, 무엇이 무엇에게 영향을 얼만큼 주고 있는가?)
1. 통계 기초
통계 : 통할 통, 셀 계
수많은 데이터를 일관된 기준이나 하나의 체계로 모아 전체적인 흐름이나 규모를 파악하는 행위
📌 모집단과 표본
- 모집단 : 통계학에서 알고자 하는 대상 전체
- 표본 : 모집단의 일부
2. 기술통계 VS 추론통계
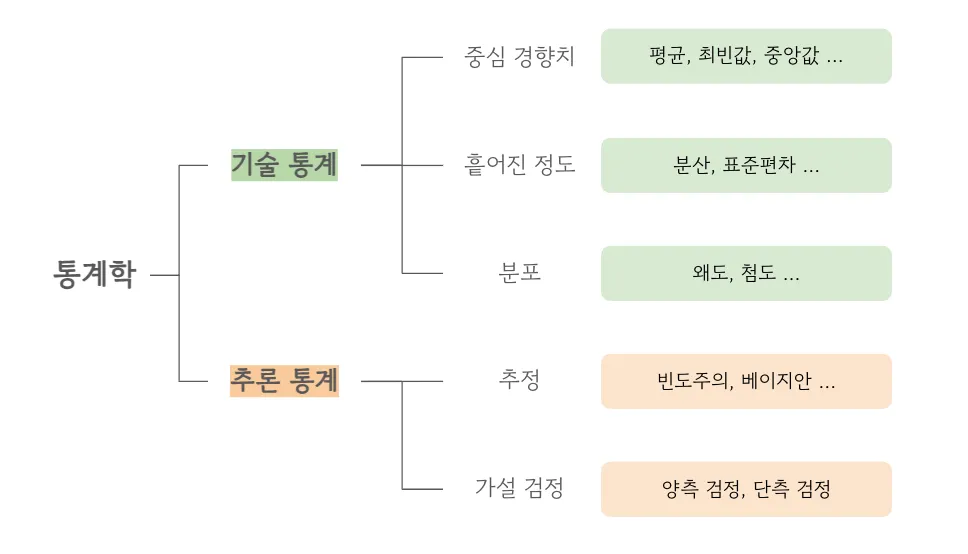
📊 기술통계(Dsecriptive statistics)
중심경향치 : 평균, 중앙값, 최빈값
- 흩어진 정도 : 분산, 표준편차
- 모집단 분산 : 각 데이터가 평균에서 얼마나 떨어져 있는지
- 표준편차 : 분산에 루트를 씌운 값
📈 시각화 예시
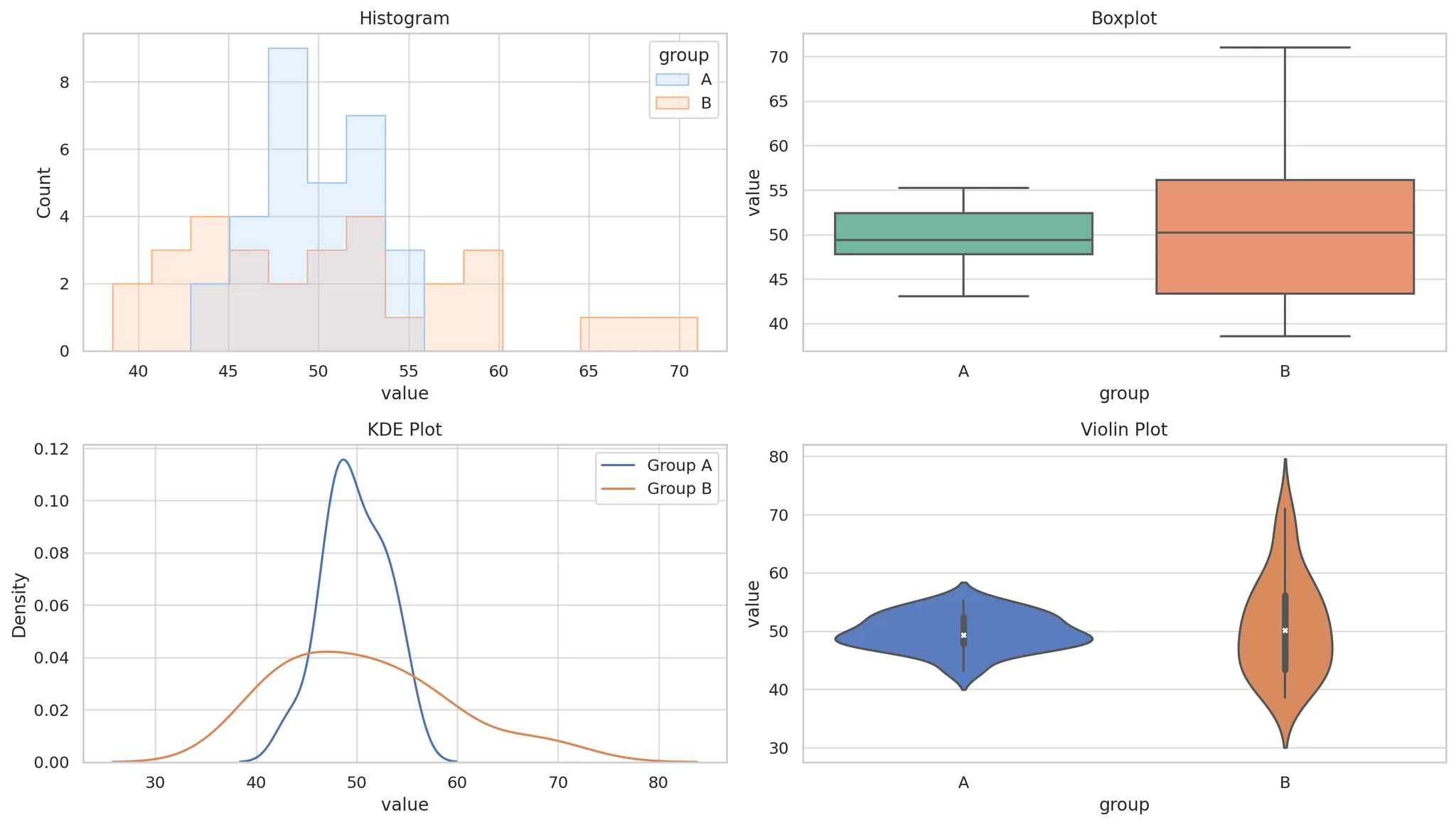
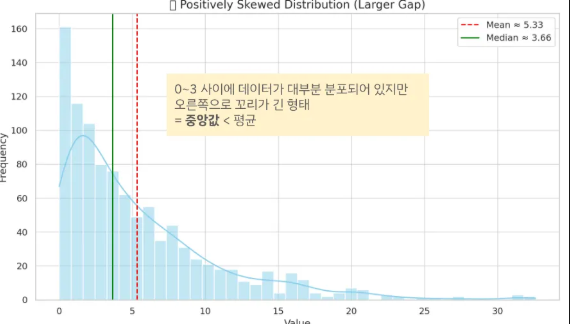
📉 분포
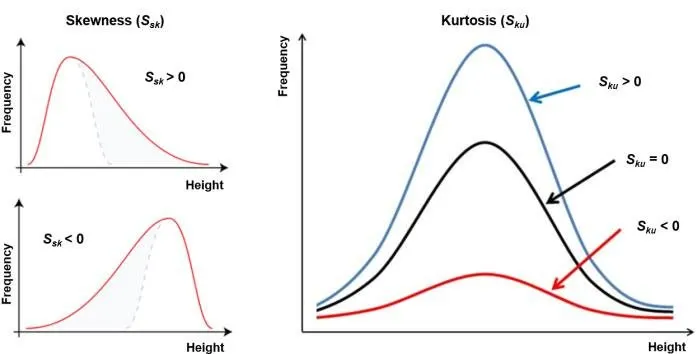
- 왜도 : 데이터 분포의 좌우 비대칭성을 나타내는 척도
- 첨도 : 뾰족함이나 완만함의 정도를 나타내는 척도
3. 추론통계
표본을 바탕으로 전체 모집단을 추정하거나 어떤 주장이 맞는지 검정하는 통계
4. 확률 기초
확률 : 발생 여부가 불확실한 사건의 발생 가능성을 숫자로 표현한 것
🎲 확률분포
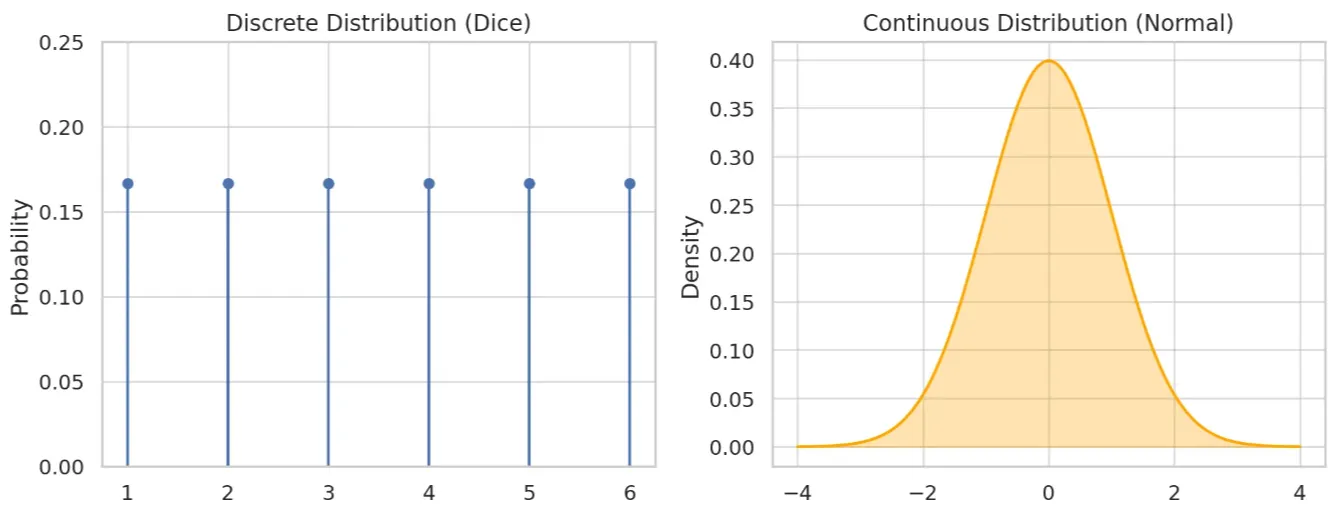
확률변수가 가질수 있는 값과 그에 대한 발생 확률간의 관계를 정리한것
- 이산형 : 셀수 있는 값 -막대그래프
- 연속형 : 실수처럼 연속적인 값 -부드러운 곡선
📚 조건부 확률
- 동시확률분포(확률변수가 2개일때)
- 독립 : 2개의 확률변수에 대한 동시확률분포
p(x,y) = p(x)*p(y)
- 독립 : 2개의 확률변수에 대한 동시확률분포
조건부 확률 공식
P(A|B) = P(A ∩ B) / P(B)
5. 추론통계 (정리)
표본의 평균과 변동성을 이용해 모집단의 특성을 추정하고 관찰된 차이가 우연인지 판단하는 과정
🔍 추정
모집단의 평균, 비율등을 알수 없기에 '표본'을 통해 추정
하나의 값만이 아니라 범위로 말하는것이 더 정확(=신뢰구간)
✅ 가설검정
어떤 주장이 우연인지 아니면 통계적으로 의미있는지를 검정하는 과정
6. 정규분포
중앙에 값이 몰리고 양 끝으로 갈수록 희박해지는 자연스러운 현상분포
평균 = 중앙값 (대칭구조)
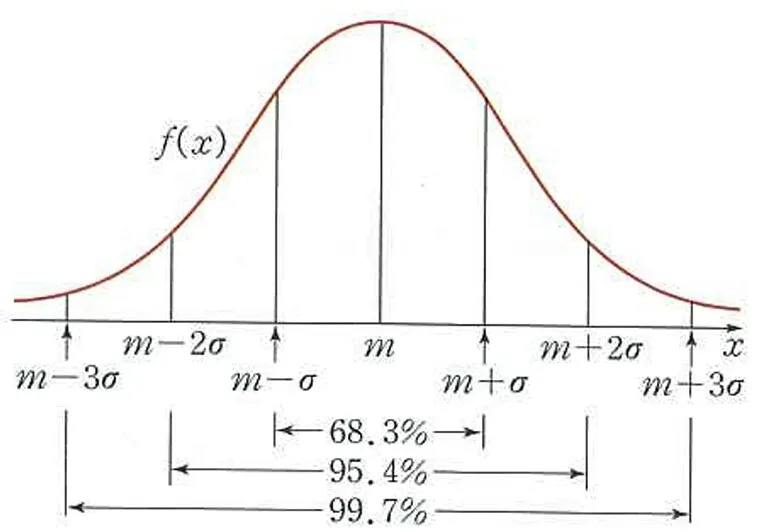
💡 정규분포 왜 중요할까?
가설검정에서 p-value를 해석할수 있는 전제가 된다.
현실의 데이터가 항상 정규는 아니지만, 모집단을 정규분포라고 가정하면 여러 통계 기법(신뢰구간,가설 검정) 등을 사용할수 있음.
표본 데이터가 정규분포가 아닌데도 모집단을 정규분포라고 가정할수 있는가?
- 표본의 크기가 충분히 클때 가능(대수의 법칙, 중심극한정리)
7. 표준화 & 표준정규분포
📏 표준화
예시) 시험점수 90점과 키 182cm 서로 다른 기준이라 비교하기 어려움, 표준화를 하면 같은 단위(z)로 변환됨 -> 표준화
이제 두 값을 상대적인 위치 기준으로 직접 비교할수 있음.
📌 표준정규분포
평균0, 표준편차1인 정규분포