통계 라이브세션 2회차
2강 : 신뢰구간과 가설검정
1. 추정
빈도주의 : 반복했을때 평균적으로 어떤 결과가 나올지 생각
베이지안 : 주어진 정보에서 얼마나 확신할수 있는지를 표현
모집단과 표본
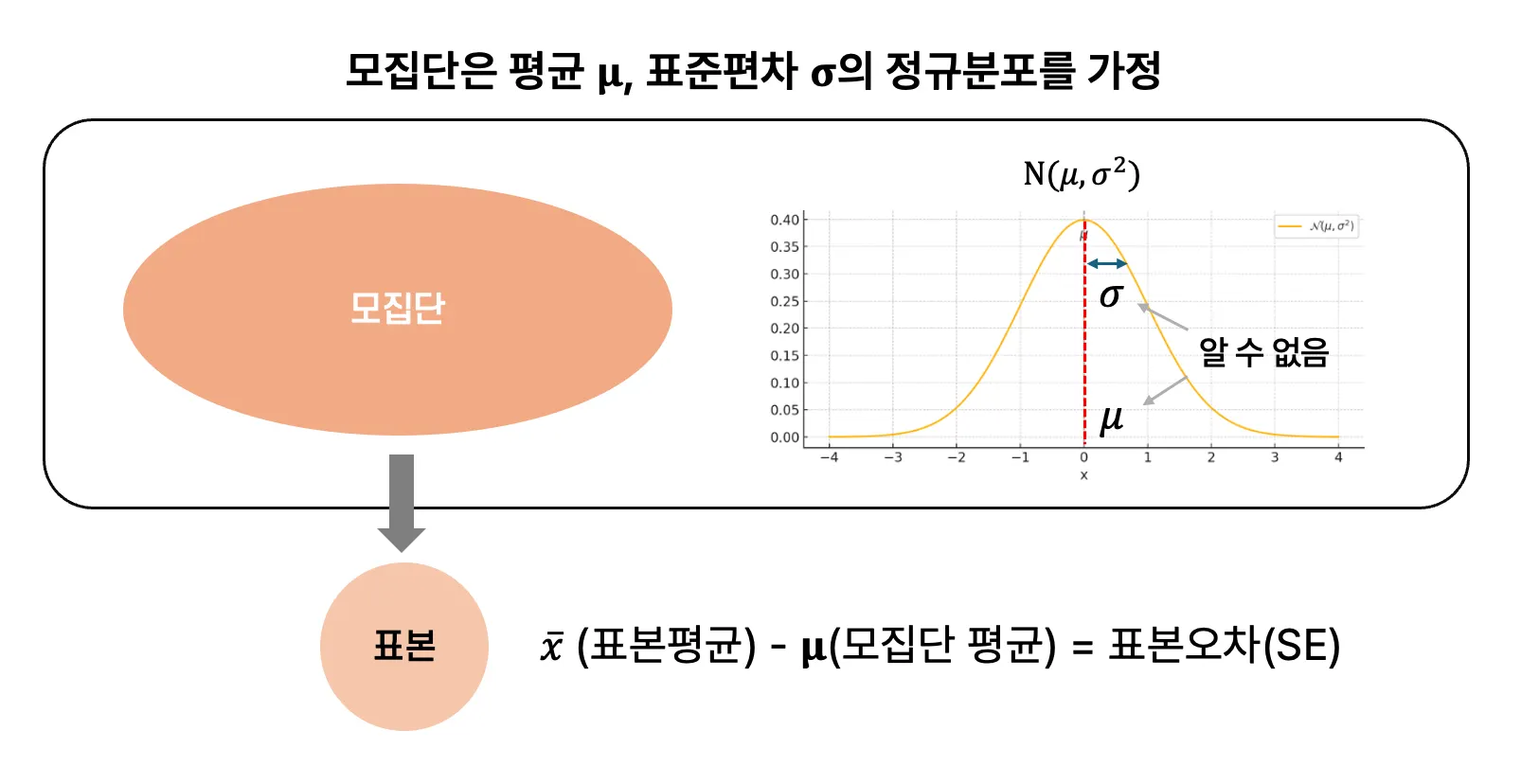
평균 μ(뮤), 표준편차 σ(시그마)
- 표본오차 : 표본 평균과 모집단 평균의 차이
- 표준오차 : 표본평균이 얼마나 흔들리는가(변동성)를 나타내는 지표
-> 표본이 커질수록 표준오차는 작아진다(1,000개의 모집단에서 100개 표본보다 900개 표본이 모집단의 평균에 더 가까움)
⭐ 표본평균의 분포
표본평균은 표본마다 달라도 그 분포는 일정한 규칙을 가진다.
표본오차도 정규분포이다.
✅ 왜 정규성 가정이 중요할까?
앞으로 배울 많은 통계기법들이 정규분포 기반으로 만들어짐
모집단이 정규가 아니어도 중심극한정리가 표본평균을 정규에 가깝에 만들어 주기 때문에 실제 분석이 가능하다는것
그럼에도 표본이 너무 왜곡되어 있거나 이상치가 많은경우 주의해야함
2. 신뢰구간(confidence interval)
표본평균이 모집단 평근의 점추정값 이지만, 단 하나의 숫자로는 불확실성을 담을수 없음.
표본 오차에 대한 정규분포
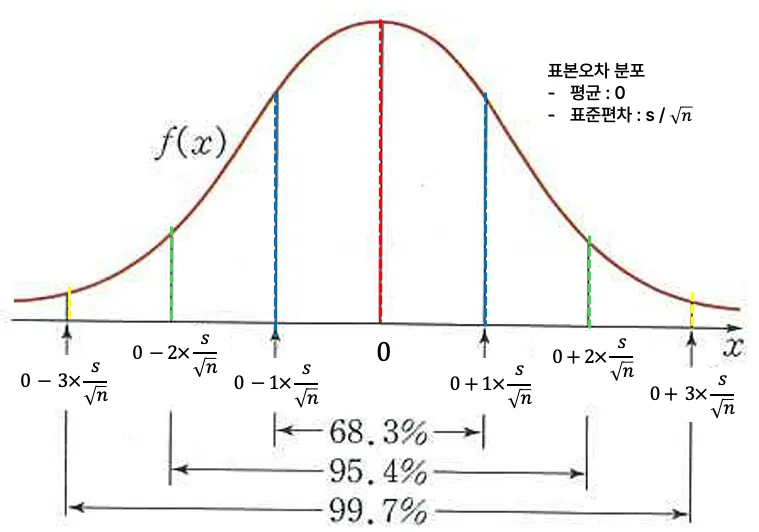
신뢰구간, 어떻게 해석할수 있을까?
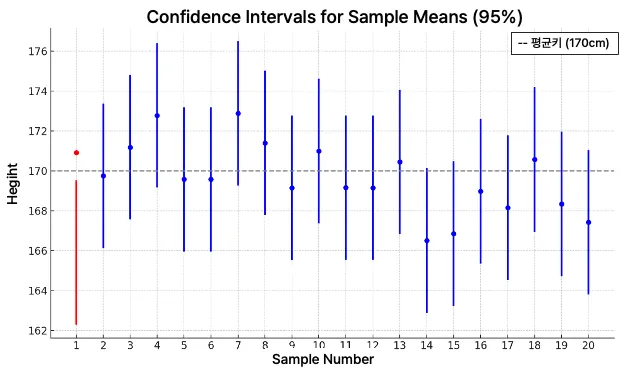
- 예시 : 남성 평균 키 추정
20번의 한번 꼴로 신뢰구간에 모집단의 평균이 포함되지 않는다.
z분포 기반 신뢰구간
평균0,표준편차 1인 정규분포를 표준화하면 언제나 z-분포가 된다.
z 값을 사용하는 이유 -> 공정한 상대적 위치 비교가능, 정규분포에서 해석이 쉬움.
t분포
추가적인 불확실성을 반영해주는 분포가 t분포
3. 가설검정
신뢰구간이 모수의 추정범위를 판단했다면 가설검정은 어떤 주장이 통계적으로 의미가 있는가를 판단.
실험군과 대조군을 비교해 가설검정
- 확증적 자료분석 : 미리 세운 가설을 검증하는 접근법
- 탐색적 자료분석 : 가설을 미리 세우지 않고 전체 데이터를 탐색적으로 해석하는 접근법
가설검정의 구조
1) 귀무가설(h0) - 밝히고자 하는 가설의 부정명제 : 두 그룹의 클릭륙 차이는 없다.
2) 대립가설(h1) -밝히고 싶은 가설 : 두 그룹의 클릭률 차이는 있다.
3) 검정통계랑 : (a-b)의 차이를 표준오차로 나눈값
4) 유의수준 : 보통 0.05%
5) p-value : 실제 데이터에서의 차이가 우연히 나올 확률
6) 판단기준 : p-value < 0.05 → H₀ 기각 (차이 유의함)
p-value
귀무가설이 맞다고 가정했을때 지금과 같은 데이터가 나올 확률
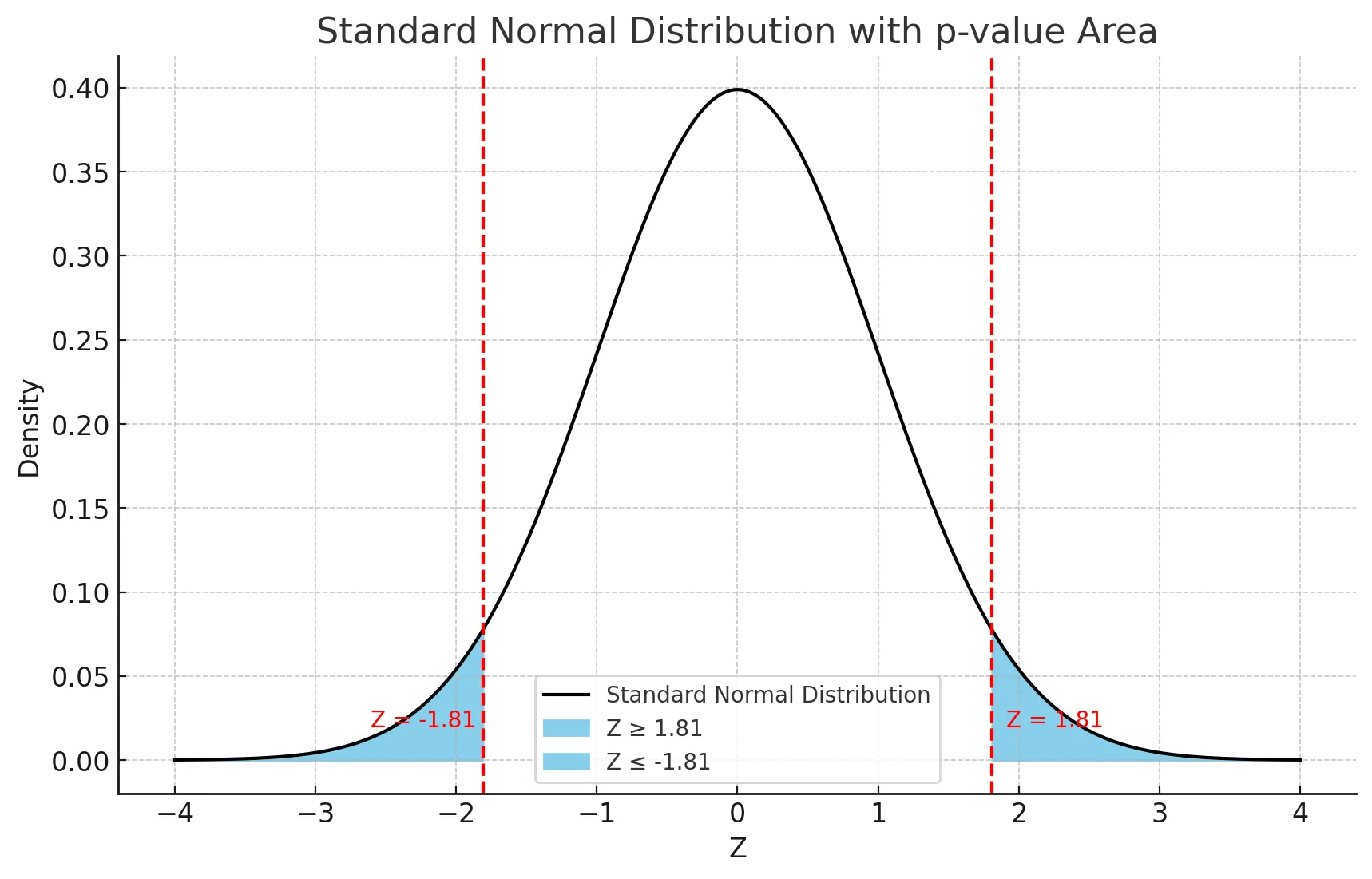
- p-value < α → 귀무가설 기각
- p-value ≥ α → 귀무가설 기각 못함
제1종 오류와 제2종 오류
가설검정은 표본 데이터를 바탕으로 판단하기 때문에 틀린 결과가 나올수 있다.
제1종오류
사실은 효과가 없는데(귀무가설이 맞는데) 있다고 판단하는 오류
아무변화가 없는데 있다고 잘못판단(false postive)
제2종 오류
사실은 효과가 있는데(대립가설이 맞는데) 없다고 판단하는 오류
변화가 있는데 없다고 잘못 판단하는 실수(false negative)
제1종오류가 중요한 상황
잘못 긍정하면 큰 손해가 나는분야
- 신약이 효과가 없는데 있다고 판단해 출시
- 금융거래에서 사기거래가 아닌데 판단해 거래정지
제2종 오류가 중요한 상황
진짜 효과를 놓치면 큰 손해가 나는 경우
- 질병이 있는데 이상없음으로 판단하는 상황
- 진짜 화재인데 경보가 안울리는 경우