👋 룩업 작업을 효율적으로 할 수 있는 "해시 테이블"에 대해 알아보자!
✏️ 해시 테이블 Hash Table
✔️ 룩업 look up
룩업 (look up)이란, 특정 원소가 컨테이너에 있는지 확인하거나 또는 컨테이너에서 특정 키에 해당하는 값을 찾는 작업이다. 룩업 작업을 시행할 때 선형 검색을 하게 된다면 O(N)의 시간 복잡도를 가진다.
이 경우, 저장된 값이 많아질 수록 작업 시간이 매우 느려져 좋지 못한 방법이다.
BST와 같은 속성을 갖도록 높이 균형 트리에 데이터를 저장하는 경우는 O(NlogN)의 시간 복잡도를 가진다. 선형 탐색보다는 훨씬 빨라지지만 이 정도 연산 속도보다 더욱 효율적인 방법을 찾고싶다!
이 때, 우리가 사용할 수 있는 효율적인 자료구조 중 하나가 바로 "해시 테이블" 이다.
✔️ 해싱 Hashing
해싱은 해시 테이블의 가장 핵심이 되는 개념으로, 각각의 데이터를 가급적 고유한 숫자 값으로 표현하고, 나중에 같은 숫자 값을 사용하여 데이터의 유무를 확인하거나 또는 해단 숫자에 대응하는 원본 데이터를 추출하는 작업이다.
또한 주어진 데이터로부터 고유한 숫자 값을 계산하는 함수를 해싱 함수라고 한다.
해시 함수의 예시로 가장 간단한 모듈로 함수(modulo function)에 대해 알아보며 해시 테이블의 특징에 대해 자세히 알아보자.
✔️ 모듈로 함수 Modulo Function
모듈로 함수는 가장 간단한 해시 함수 중 하나로, 큰 범위의 정수를 인자로 받아 정해진 정수(n)으로 나눈 나머지를 해시 값으로 반환하는 함수이다. 나머지 연산은 보통 % 기호로 표시한다.
이 함수를 사용하는 경우, 주어진 입력값을 x라고 했을 때, x의 값을 배열의 x%n 위치에 삽입하면 된다.
예를 들어, n값이 7인 모듈로 함수에서 입력값 10이 들어왔다면 10은 array[3]에 저장된다.
❗ 모듈로 함수의 문제점
모듈로 함수에서는 서로 다른 데이터에 대해 같은 해시 값을 반환할 수 있다는 문제점이 존재한다. 위에서 예시로 든 n 값이 7인 함수인 경우 9 % 7과 16 % 7 의 값은 모두 2로 동일하다. 즉 두 데이터 모두 array[2]의 위치에 저장해야 하기 때문에 충돌 (Collision)이 발생한다.
이처럼 충돌이란 해시 함수가 서로 다른 키에 대해 같은 해시 값을 반환함으로써, 다수의 키가 같은 값을 갖게 되는 현상을 말한다.
우선 충돌 상황을 고려하지 않는 모듈로 함수를 C++에서 구현해보도록 하자.
❗ 모듈로 함수를 이용한 해시 맵 구현 (충돌 고려 X)
#include <iostream>
#include <vector>
using namespace std;
using uint = unsigned int;
class hash_map {
vector<int> data;
int size;
public:
hash_map(size_t n) {
size = n;
data = vector<int>(n, -1); //벡터의 크기는 n이고, 벡터의 모든 원소를 -1로 초기화
}
void insert(uint value) {
data[value % size] = value;
cout << value << "을(를) 삽입했습니다.\n";
//충돌에 대한 처리를 따로 해주지 않아 해시 값이 중복되는 경우 마지막에 삽입한 값만 저장됨
}
void find(uint value) {
if (data[value % size] == value) cout << value << "을(를) 찾았습니다.\n";
else cout << value << "을(를) 찾지 못했습니다.\n";
}
void erase(uint value) {
if (data[value % size] == value) {
data[value % size] = -1;
cout << value << "을(를) 삭제했습니다.\n";
}
}
};
int main() {
hash_map map(7);
map.insert(20);
map.insert(18);
map.insert(77);
map.find(77);
map.find(1000);
map.erase(20);
map.find(20);
return 0;
}앞서 언급했듯 위 코드에서는 충돌을 고려해주지 않기 때문에 충돌이 발생한 경우, 동일한 위치에 가장 나중에 삽입되는 데이터만 남게 된다.
그렇다면 이러한 충돌 문제를 해결하기 위한 방법으로는 무엇이 있을까?
✏️ 해시 테이블에서의 충돌
✔️ 체이닝 Chaining
충돌 문제를 해결하기 위한 방법 중 첫번째는 "체이닝 Chaining" 이다.
체이닝은 해시 테이블의 특정 위치에 하나의 키를 저장하는 것이 아니라, 하나의 연결 리스트를 저장하여 동일 키에 대한 여러 값을 저장할 수 있는 방법이다.
새로 삽입된 키에 의해 충돌이 발생하는 경우 리스트의 맨 뒤에 새로운 키를 추가한다. 이 때, 벡터 대신 연결 리스트를 사용하는 이뉴는 특정 위치의 원소의 삭제 연산을 빠르게 처리하기 위함이다. 연결 리스트는 따로 구현하지 않고 STL의 std::list를 이용하였다.
#include <iostream>
#include <vector>
#include <list>
#include <algorithm>
using namespace std;
using uint = unsigned int;
class hash_map {
vector<list<int>> data;
int size;
public:
hash_map(int n) {
data.resize(n); //벡터의 size를 n으로 할당하고
size = n;
}
void insert(uint value) {
data[value % size].push_back(value);
cout << value << "을(를) 삽입했습니다.\n";
}
bool find(uint value) {
list<int>& check = data[value % size];
return std::find(check.begin(), check.end(), value) != check.end();
}
void erase(uint value) {
list<int>& check = data[value % size];
auto iter = std::find(check.begin(), check.end(), value);
if (iter != check.end()) { //값을 찾은 경우
check.erase(iter);
cout << value << "을(를) 삭제했습니다.\n";
}
else cout << "삭제할 값을 찾지 못했습니다.\n";
}
};
int main() {
hash_map map(7);
auto print = [&](int value) { //람다함수
if (map.find(value)) cout << "해시 맵에서 " << value << "을(를) 찾았습니다.\n";
else cout << "해시 맵에서 " << value << "을(를) 찾지 못했습니다.\n";
};
map.insert(2);
map.insert(7);
map.insert(9);
map.insert(20);
print(9);
print(20);
map.erase(100);
map.erase(2);
print(2);
return 0;
}❗ Chaining 방법 사용시 시간복잡도
삽입 함수의 시간복잡도는 O(1)이고, 리스트에 값을 push_back 하는 것이 단순히 벡터의 값을 설정하는 것 보다는 조금 느릴 수 있지만 유의미 하지 않다.
하지만 룩업과 삭제의 경우는 데이터 크기와 해시 테이블 크기에 따라 상당히 느릴 수 있다. 예를 들어, 모든 키가 같은 해시 값을 가지는 경우 룩업 연산은 연결 리스트에서의 선형 검색과 동일하므로 O(N)의 시간복잡도를 가진다.
해시 테이블이 저장할 키 개수에 비해 매우 작다면 충돌이 많이 발생하게 되고, 각 키 값에 대한 연결 리스트 또한 길어지게 된다. 반대로 데이터에 비해 너무 큰 해시 테이블을 가지고 있으면 메모리 낭비가 발생하게 된다. 따라서 해시 테이블을 이용할 때에는 적절한 크기를 가지는 것이 중요하다.
이를 위해 각각의 리스트에 저장되는 키의 평균 개수를 나타내는 부하율 (Load Factor)을 사용할 수 있다.
부하율 = 전체 키의 개수 / 해시 테이블 크기
- 부하율 == 1 : 전체 키의 개수와 해시 테이블의 크기가 같은 매우 이상적인 상태
모든 연산이 O(1)에 가깝에 작동하며 메모리 공간을 적절하게 활용 - 부하율 < 1 : 키가 하나도 저장되지 않은 리스트가 존재한다는 뜻으로 메모리 낭비 가능성 O
- 부하율 > 1 : 리스트의 평균 길이가 1보다 크다는 뜻으로 검색, 삭제 등의 함수 소요 시간 ↑
부하율이 해시테이블의 성능을 결정하는 유일한 지표는 아님을 주의하자!
✔️ 열린 주소 지정 Open Addressing
충돌 문제를 해결하기 위한 또 다른 방법으로 "열린 주소 지정 Open Addressing"이 있다.
이는 Chaining과 달리 모든 데이터 값을 해시 테이블 내에 저장한다. 따라서 항상 해시 테이블의 크기가 데이터의 개수보다 커야 한다. Open Addressing의 핵심은 특정 해시 값에 해당하는 위치가 이미 사용되고 있따면 테이블의 비어있는 다른 위치를 탐색하는 것이다.
그렇다면 비어있는 다른 위치를 탐색하는 방법은 무엇이 있을까?
❗ 선형 탐색 Linear Probing
선형 탐색은 가장 간단한 탐색 방법이다. 특정 해시 값에서 충돌이 발생하는 경우, 해당 위치에서 한 칸 뒤로 차례로 이동하며 비어있는 셀을 찾으면 원소를 삽입한다.
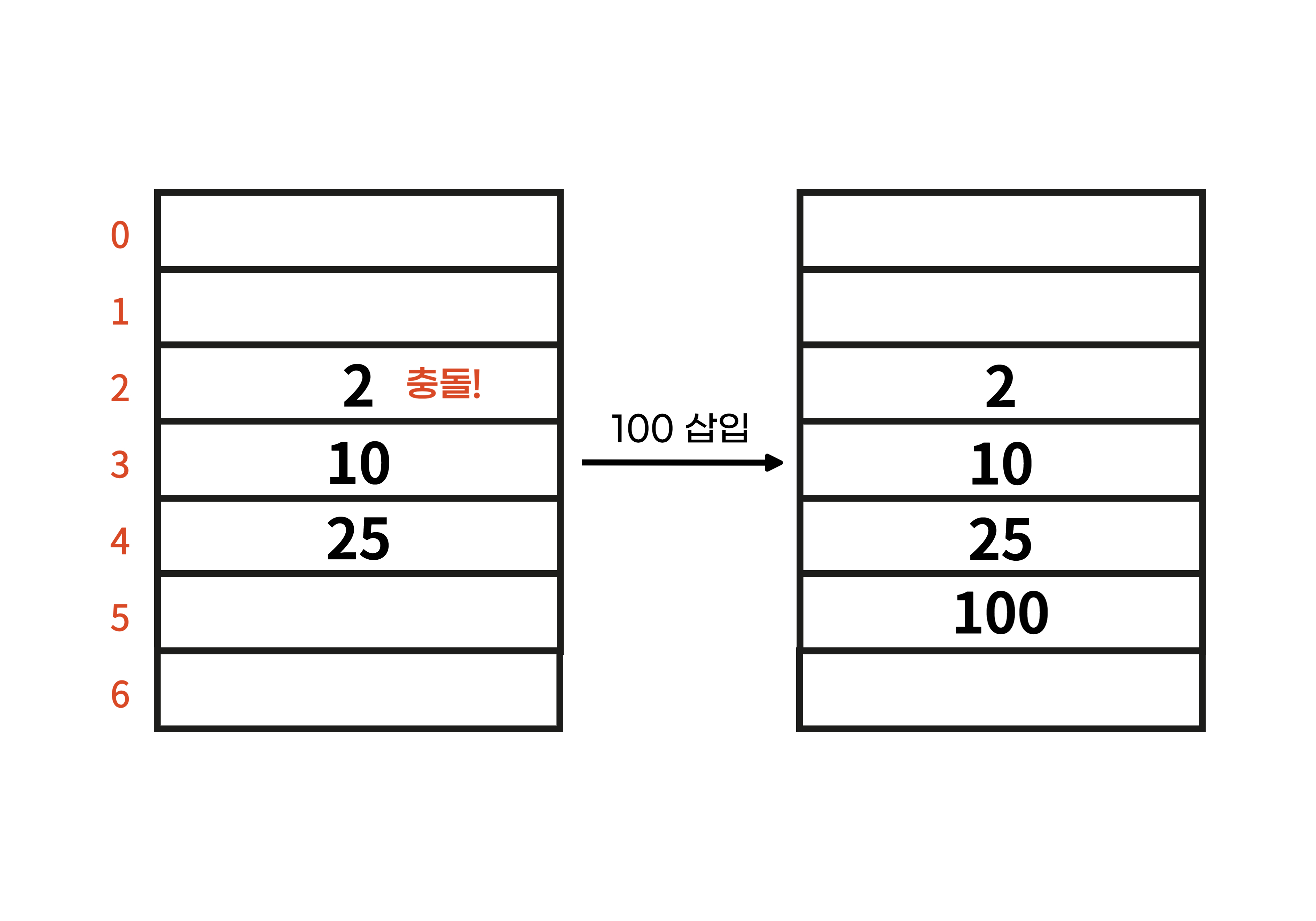
위의 예시에서 해시 맵에 100을 삽입하는 경우, 그 해시 값이 2로 원래 해당 위치에 존재하던 2와 충돌이 발생한다. 이후 차례로 hash[3], hash[4]를 탐색하며 빈 공간인 hash[5]에 100의 값이 저장된다.
이러한 선형 검색에는 문제점이 존재하는데, 바로 군집화 (Clustering)이다.
선형 검색을 통해 충돌하는 값을 다른 위치에 저장하는 경우 서로 인접한 군집 형태로 갑시 채워진다. 특정 해시 값이 너무 자주 발생하여 데이터가 몇 개의 그룹으로 뭉치는 형태로 저장된는 것을 군집화라고 한다. 군집화가 발생하는 경우, 원소 검색 시 군집에 대한 선형 검색이 발생하여 검색 속도가 크게 느려진다는 문제점이 있다. 예를 들어, 위의 예시에서 100을 검색하고자 하는 경우 2가 저장된 위치에서부터 차례로 선형 검색을 통해 100이 저장된 위치까지 탐색을 진행해야 한다. 군집이 커진다면 검색 속도가 급격하게 늘어날 것이다.
군집화의 확률을 낮추기 위해서 선형 탐색 대신 이차함수 탐색을 적용하기도 한다.
❗ 이차함수 탐색 Quadratic Probing
선형 탐색의 가장 큰 문제점이었던 군집화의 확률을 줄이고자, 선형 방정식이 아닌 이차 방정식으로 사용하여 탐색을 수행할 수 있는데 이를 이차함수 탐색이라고 한다.
예를 들어, 데이터를 hash(x) 위치에 삽입하려는데 충돌이 발생하는 경우 hash(x+1^2)으로 이동하고, 그 다음은 hash(x+2^2)위치로 이동한다. 이처럼 이동 폭을 이차함수 형태로 증가시켜 데이터 군집이 나타날 확률을 줄일 수 있게 되는 것이다.
선형 탐색과 이차함수 탐색 모두 원소의 위치가 기존에 삽입되어 있는 다른 원소에 의해 영향을 받는다는 특징이 있다. 또한 특정 해시 값을 갖는 키가 오직 하나만 존재한다 하더라도 충돌이 발생할 수 있다.
작년에 학부 알고리즘 수업에서 해시 테이블을 배웠었는데, 제대로 이해하지 못하고 넘어갔던 기억이 있다. 확실히 한 번 더 공부하니 이제야 머리 속에 정리가 된 것 같아 뿌듯하다. 효율적인 해싱 기법 중 하나인 뻐꾸기 해싱은 공부하는대로 포스팅에 내용을 추가해놓겠다! 🖐️
