👋 비선형 자료구조 "트리"에 대해 알아보자!
✏️ 트리 Tree
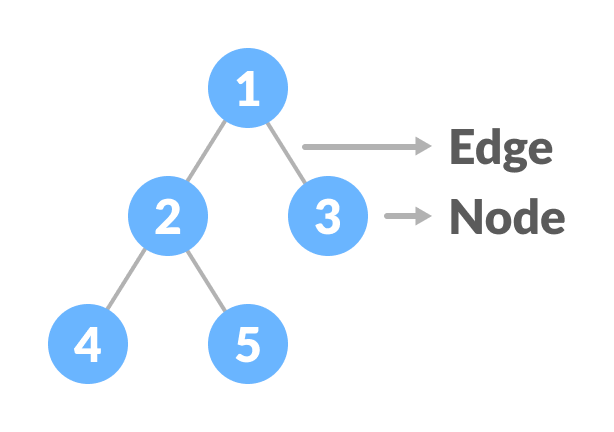
트리는 노드와 노드 사이를 연결하는 edge를 이용하여 계층을 구성하는 대표적인 비선형 자료구조이다. 앞서 다루었던 선형 자료구조에서는 순방향과 역방향 순회가 가능하였지만 이러한 구조는 매우 제한적이어서 복잡한 문제에 적용하기 어렵다. 대표적으로 계층적 문제나 순환 종속성 문제등이 선형 자료구조를 사용하기 어려운 문제들이다.
이러한 문제를 풀기 위해 다양한 비선형 자료구조들이 존재하며,
오늘은 그 중 트리에 대해 다루어보고자 한다!
✔️ 트리의 특징
- 구성 요소
- 노드 node : 데이터가 저장된 부분
- 엣지 edge: 노드와 노드를 연결하는 선
- 루트 노드 root node : 최상단에 위치한 노드로 부모 노드가 없는 노드
- 리프 노드 leaf node : 최하단에 위치한 노드로 자식 노드가 없는 노드
- terminal node, external node, 단말 노드라고 부르기도 함
- 비단말 노드 internal node : 자식 노드가 있는 노드
- 형제 노드 sibling node : 같은 부모를 가지는 노드들
- 특징 용어
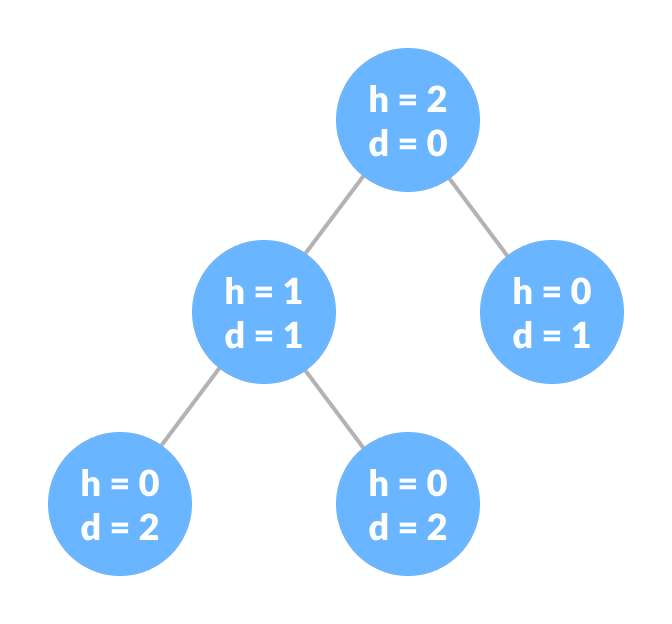
- 높이 height : 자신 → 리프노드까지의 최대 엣지 수
- 트리의 높이 = 루트노드의 높이 - 깊이 depth : 루트 노드 → 자신까지의 최대 엣지 수
- degree : 노드의 자식 수 (서브트리의 수)
- 높이 height : 자신 → 리프노드까지의 최대 엣지 수
-
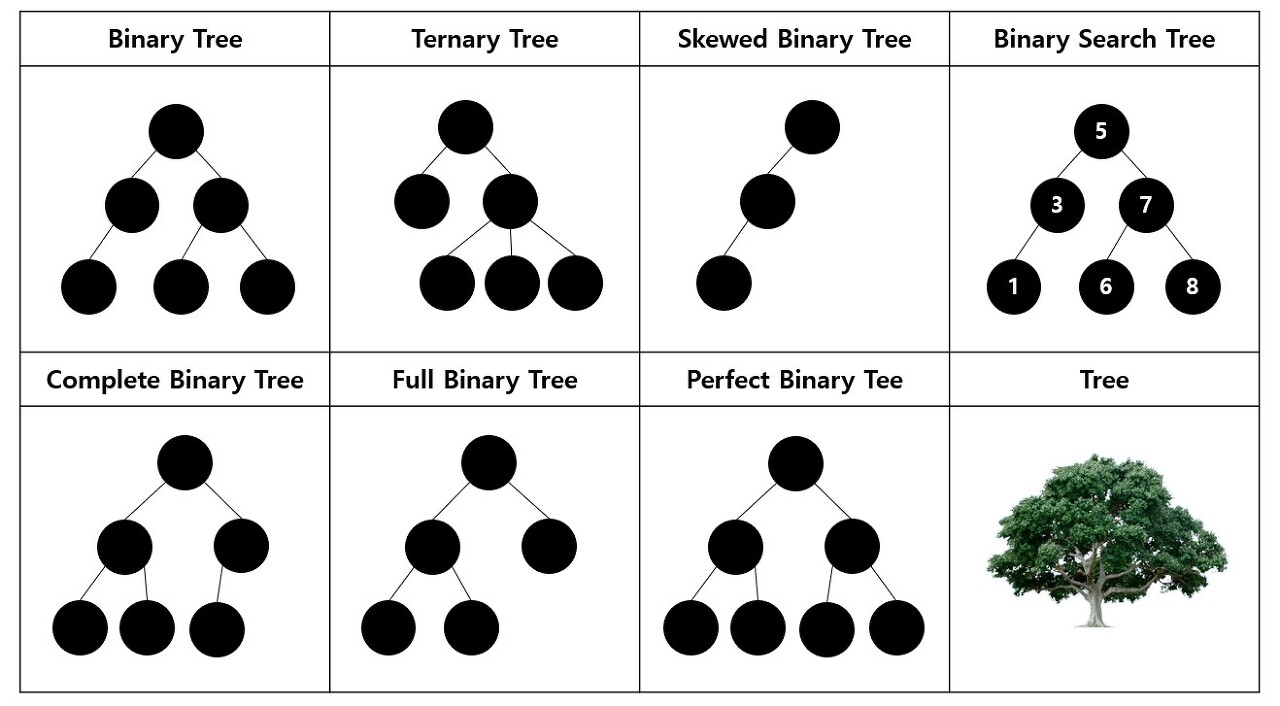
트리의 종류
- Binary Tree : 각 노드당 자식 노드의 개수가 최대 2개로 제한된 트리
- Ternary Tree : 각 노드당 자식 노드의 개수가 최대 3개로 제한된 트리
- Skewed Binary Tree : 높이에 대한 최소 노드를 가지면서 한쪽 방향의 자식노드만 가지는 트리
- Binary Search Tree : 각 노드의 왼쪽 서브트리는 현재 노드의 데이터보다 작은 값이,
오른쪽 서브트리는 현재 노드의 데이터보다 큰 값이 저장되는 이진 트리 - Full Binary Tree : 모든 노도의 자식 노드의 수가 2개 혹은 0개인 이진 트리
- Perfect Binary Tree : 모든 리프 노드의 depth가 동일한 Full Binary Tree
- Complete Binary Tree : 리프 노드를 제외한 트리 부분은 Perfect Binary Tree 이면서,
리프노드들이 왼쪽에서부터 차례로 저장되어 있는 이진 트리
Full, Perfect, Complete 헷갈리지 않게 구분 잘 할 것
+) Balanced Binary Tree에 대해서는 따로 포스팅을 할 예정이다!
✏️ 트리 구현하기 (C++)
❗ 이진 탐색 트리 Binary Search Tree 구현
#include <iostream>
#include <string>
//memoey leak 확인
#define _CRTDBG_MAP_ALLOC
#include <stdlib.h>
#include <crtdbg.h>
using namespace std;
struct Node { //노드 구조체
int data;
Node* left_child;
Node* right_child;
};
class BinarySearchTree {
public:
Node* root;
int tree_size;
BinarySearchTree() { //생성자
this->root = NULL;
tree_size = 0;
}
~BinarySearchTree() {
_CrtDumpMemoryLeaks();
}
Node* deleteAll(Node* root) { //new로 동적할당 된 메모리의 해제
if (root == NULL) return NULL;
deleteAll(root->left_child);
deleteAll(root->right_child);
delete[] root;
}
Node* createNode(int data) { //새 노드 메모리 동적할당 및 초기화
Node* new_node = new Node;
new_node->data = data;
new_node->left_child = NULL;
new_node->right_child = NULL;
return new_node;
}
void addNode(int data) { //삽입될 위치에 새 노드 삽입
Node* new_node = createNode(data); //노드 생성
Node* temp = this->root;
if (temp == NULL) { //트리가 비어있는 경우
this->root = new_node;
tree_size++;
cout << "Successfully Add New node " << data << "\n";
}
else {
while (true) {
if (temp->data >= data) {
if (temp->left_child == NULL) {
temp->left_child = new_node;
tree_size++;
break;
}
else temp = temp->left_child;
}
else if (temp->data < data) {
if (temp->right_child == NULL) {
temp->right_child = new_node;
tree_size++;
break;
}
else temp = temp->right_child;
}
}
cout << "Successfully Add New node " << data << "\n";
}
}
void treeSize() { //트리의 노드 개수 출력
cout << "Size of BST: " << this->tree_size << "\n";
}
Node* findNode(Node* temp, int data) { //인자로 받은 값을 가지는 노드가 트리에 있는지 확인
if (temp == NULL) {
cout << "Fail to find the data!\n";
return NULL;
}
else if (temp->data == data) {
cout << "Find the data!\n";
return temp;
}
else if (temp->data > data) findNode(temp->left_child, data);
else if (temp->data < data) findNode(temp->right_child, data);
}
Node* deleteNode(Node* root, int data) { //인자로 주어지는 값을 가지는 노드 삭제
if (root == NULL) return root;
if (root->data > data) root->left_child = deleteNode(root->left_child, data);
else if (root->data < data) root->right_child = deleteNode(root->right_child, data);
else { //root->data == data
Node* temp;
this->tree_size--;
if (root->left_child == NULL) temp = root->right_child;
else if (root->right_child == NULL) temp = root->left_child;
else {
temp = findMinNode(root->right_child);
temp->left_child = root->left_child;
}
if (this->root == root) this->root = temp;
delete[] root;
return temp;
}
}
Node* findMinNode (Node* root) {
Node* temp = root;
while (temp->left_child != NULL) temp = temp->left_child;
return temp;
}
Node* inorderTraversal(Node* root) { //중위순회
if (root == NULL) return NULL;
inorderTraversal(root->left_child);
cout << root->data << ' ';
inorderTraversal(root->right_child);
}
Node* preorderTraversal(Node* root) { //전위순회
if (root == NULL) return NULL;
cout << root->data << ' ';
preorderTraversal(root->left_child);
preorderTraversal(root->right_child);
}
Node* postorderTraversal(Node* root) { //후위순회
if (root == NULL) return NULL;
postorderTraversal(root->left_child);
postorderTraversal(root->right_child);
cout << root->data << ' ';
}
};
int main() {
int num;
cin >> num;
string command;
BinarySearchTree bst; //이진탐색트리 클래스
for (int i = 0; i < num; i++) {
cin >> command;
if (command == "add") { //삽입
int data;
cin >> data;
bst.addNode(data);
}
else if (command == "find") { //탐색
int data;
cin >> data;
bst.findNode(bst.root, data);
}
else if (command == "delete") { //삭제
int data;
cin >> data;
bst.deleteNode(bst.root, data);
}
else if (command == "inorder") { //중위순회
bst.inorderTraversal(bst.root);
cout << "\n";
}
else if (command == "preorder") { //전위순회
bst.preorderTraversal(bst.root);
cout << "\n";
}
else if (command == "postorder") { //후위순회
bst.postorderTraversal(bst.root);
cout << "\n";
}
else if (command == "size") bst.treeSize(); //크기
else cout << "Please input right command form" << "\n"; //입력오류
}
bst.deleteAll(bst.root); //메모리 해제
return 0;
}✔️ BST 삭제 연산
BST의 여러 연산 중 가장 고려해야될 부분이 많은 것이 삭제 연산이다.
특정 노드를 삭제하는 경우, 그 노드의 자식이 1) 없는 경우, 2) 왼쪽 혹은 오른쪽 자식만 있는 경우, 3) 왼쪽 오른쪽 모두 자식이 있는 경우 총 3가지로 나누어 고려해주어야 한다.
1. 삭제 노드의 자식이 없는 경우
3가지 경우 중 가장 간단한 경우이다.
삭제할 노드가 리프 노드여서 자식이 없는 경우는 해당 노드를 delete 해주기만 하면 된다.
2. 삭제 노드의 자식이 한 개인 경우 (왼 or 오)
삭제할 노드가 1개의 자식을 가지고 있다면 자식이 삭제할 노드의 위치로 대체되면 된다.
삭제할 노드를 delete, 삭제할 노드의 유일 자식 노드를 child, 삭제할 노드의 부모 노드를 parent라고 해보자. 만약 삭제할 노드가 parent의 왼쪽 자식이었던 경우는 parent->left_child = child가 되고, 반대로 삭제할 노드가 parent의 오른쪽 자식이었던 경우는 parent->right_chlid= child가 된다.
if (root->data > data) root->left_child = deleteNode(root->left_child, data);
else if (root->data < data) root->right_child = deleteNode(root->right_child, data);위 코드에서 deleteNode 함수의 반환 값이 새롭게 parent와 연결될 child 노드이므로 삭제하고 싶은 노드만 delete되고 삭제할 노드의 서브트리는 다시 parent와 연결되어 정상적으로 삭제 연산이 진행된다.
(설명할 때는 parent로 표현하고 코드 상에서는 root로 표현하여 혼동될 수 있으니 주의 바랍니다...😭)
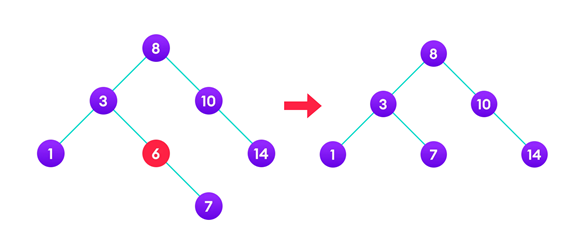
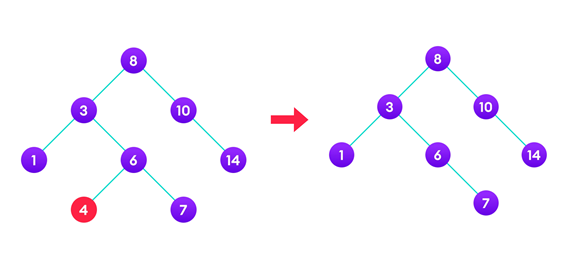
3. 삭제 노드의 자식이 두 개인 경우
삭제 연산의 3가지 상황 중 가장 복잡한 경우이지만 코드상으로는 생각보다 간단하게 구현할 수 있다.
만약 삭제할 노드가 자식을 2개 가지고 있는 경우, 과연 어떤 노드가 삭제될 노드의 자리를 대체해야 할까?
이 경우 두 가지 중 원하는 방식을 선택하여 구현하면 된다.
1) 삭제할 노드의 왼쪽 서브트리 중 최대값을 가진 노드
2) 삭제할 노드의 오른쪽 서브트리 중 최솟값을 가진 노드
이는 BST의 특징만 잘 생각해본다면 쉽게 이해할 수 있다. 아래의 예시로 설명해보도록 하겠다.
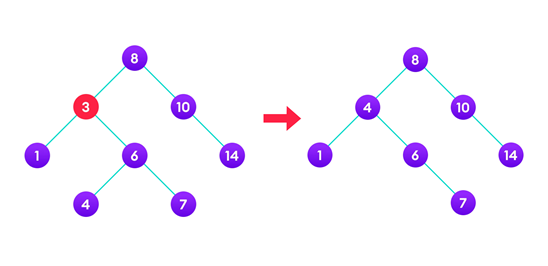
위 그림에서 우리는 3을 삭제하고자 한다. 3을 삭제하고 그 자리에 어떠한 노드를 연결시켜 주어야 하는데, BST의 특징을 생각해보았을 때 특정 노드의 왼쪽 서브트리에는 특정 노드 값보다 작은 것들이, 오른쪽에는 특정 노드 값보다 큰 값이 저장되어야 한다. 따라서 3의 왼쪽 서브 트리에 저장된 노드 중 하나를 뽑아 3 자리에 넣고 싶다면 그들 중 가장 큰 값이 뽑혀야 할 것이다. 같은 방법으로 3의 오른쪽 서브 트리에 저장된 노드 중 하나를 뽑는 경우는 그들 중 가장 작은 값이 뽑혀야 BST의 특징을 유지할 수 있게 된다.
deleteNode 함수의 반환값은 삭제할 노드 위치에 대체될 노드의 포인터 값이다. 나는 두 가지 방식 중 두 번째 방식을 선택하여 삭제할 노드의 오른쪽 서브트리 중 최소값을 가진 노드를 가리키는 포인터를 반환할 수 있도록 하였다. (findMinNode)
✔️ BST의 순회 Traversal (Inorder, Preorder, Postorder)
주어진 트리를 순회하여 노드에 접근하는 방법에는 3가지가 있다.
- 중위순회 (Inorder Traversal) 왼쪽노드 → 현재노드 → 오른쪽노드 순으로 순회
- 전위순회 (Preorder Traversal) 현재노드 → 왼쪽노드 → 오른쪽노드 순으로 순회
- 후위순회 (Postorder Traversal) 왼쪽노드 → 오른쪽노드 → 현재노드 순으로 순회
Node* inorderTraversal(Node* root) { //중위순회
if (root == NULL) return NULL;
inorderTraversal(root->left_child);
cout << root->data << ' ';
inorderTraversal(root->right_child);
}
Node* preorderTraversal(Node* root) { //전위순회
if (root == NULL) return NULL;
cout << root->data << ' ';
preorderTraversal(root->left_child);
preorderTraversal(root->right_child);
}
Node* postorderTraversal(Node* root) { //후위순회
if (root == NULL) return NULL;
postorderTraversal(root->left_child);
postorderTraversal(root->right_child);
cout << root->data << ' ';
}
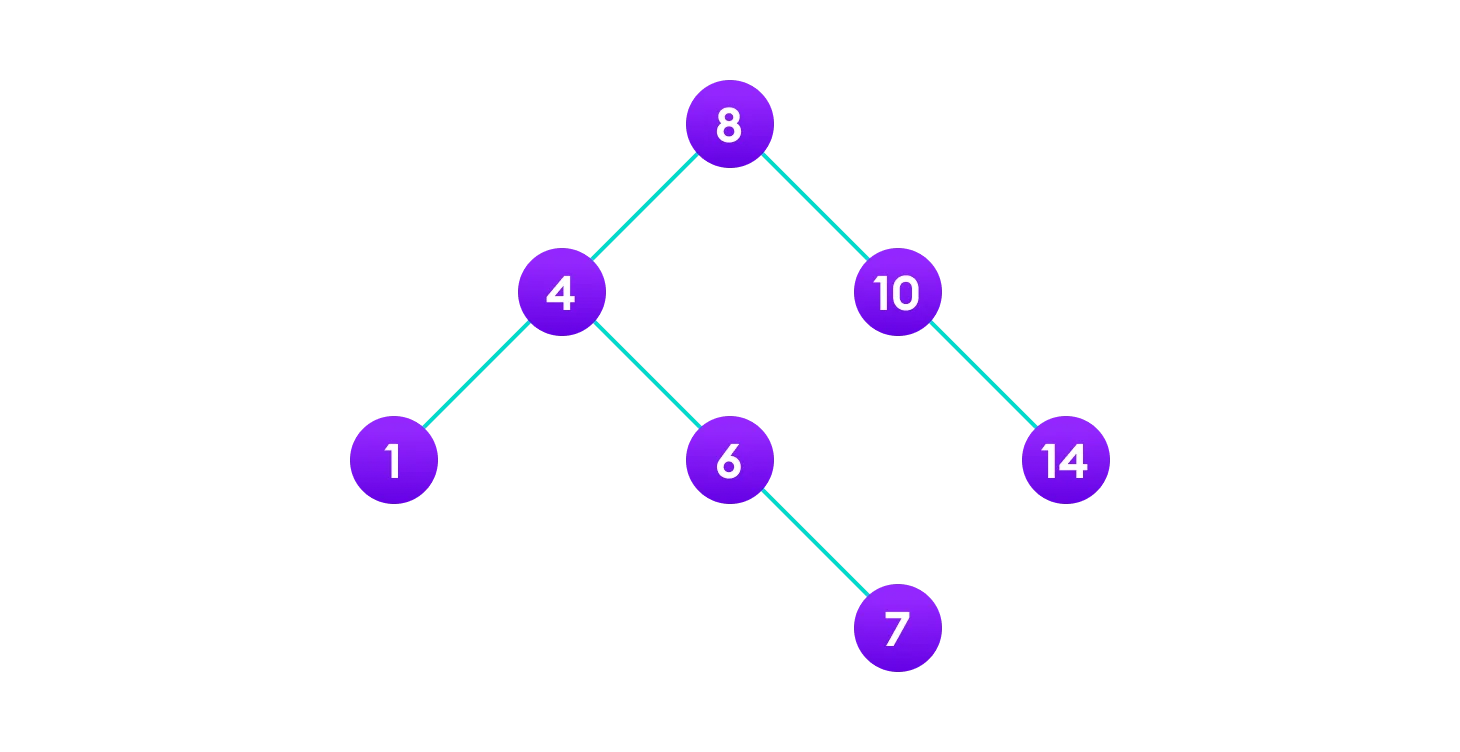
위와 같은 트리에서 중위, 전위, 후위 순회시 방문하는 노드의 순서를 알아보자.
- 중위 순회: 1 → 4 → 6 → 7 → 8 → 10 → 14
- 전위 순회: 8 → 4 → 1 → 6 → 7 → 10 → 14
- 후위 순회: 1 → 7 → 6 → 4 → 14 → 10 → 8
오늘을 트리의 특징과 구조, 종류 등에 대해 알아보고 그 중 이진탐색트리를 C++을 이용하여 구현해보았다. 전부 학부 자료구조 시간에 했었던 것인데도 구현할 때 버벅버벅거려서 약간 머쓱 ㅎㅎ...
재귀함수는 나름 수업에서도 많이 배우고 썼었어서 머리 속에서 잘 돌아갔었는데 갑자기 리셋된 느낌이 들어서 당황스러웠다 ㅋㅋㅋㅠㅠ 특히 삭제 연산에서 뭘 리턴값으로 하고 코드 구조를 어떻게 해야하는지 아주 헷갈렸당 이제 제발 까먹지 말고 평생 기억해주길 🙀
다음 번 자료구조 포스팅으로는 아마 그래프를 다룰 것 같다. 아직 트리에서도 빼놓은 것들도 많은데 (Red-Black tree, B-tree, Heap 등등) 이건 차차 보는 걸로... 공부하면 할 수록 내용이 너무 많다!!! 열심히 달려보자아 아자 아자 💪
[이미지 출처] https://www.programiz.com/dsa/trees
https://thinking-developer.tistory.com/70
