[Data Structure] Graph

그래프는 노드(Node,vertex) 그리고 노드와 노드를 연결하는 간선(edge)으로 구성 됩니다.
그래프는 무방향 일수 있습니다. 이는 간선에 의해 연결된 2개의 노드가 대칭일 수 있다는 의미 입니다. 한편 방향성을 가질 수도 있는데, 이는 비대칭 관계를 의미 합니다.

• 깊이 우선 탐색
  루트 노드에서 시작해서 다은 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
  넓게(wide) 탐색하기 전에 깊게(deep) 탐색하는 것이다.
• 너비 우선 탐색
  루트 노드에서 시작해서 인접한 노드를 먼저 탐색하는 방법
  즉, 깊게(deep) 탐색하기 전에 넓게(wide) 탐색하는 것이다.

• 그래프는 네트워크 모델 이다.
• 2개 이상의 경로가 가능하다.
  즉, 노드들 사이에 무방향/방향에서 양방향 경로를 가질 수 있다.
• self-loop 뿐 아니라 loop/circuit 모두 가능하다.
• 루트 노드라는 개념이 없다.
• 부모-자식 관계라는 개념이 없다.
• 순회는 DFS나 BFS로 이루어진다.
• 그래프는 순환(Cyclic) 혹은 비순환(Acyclic)이다.
• 그래프는 크게 방향 그래프와 무방향 그래프가 있다.
• 간선의 유무는 그래프에 따라 다르다.

그래프 구현 2가지

1. 인접 리스트
   인접 리스트(Adjacency List)로 그래프를 표현하는 것이 가장 일반적인 방법 이다.
   
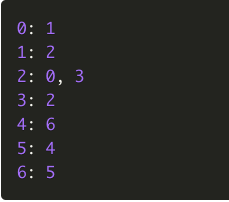
2. 입접 행렬
   인접행렬은 행렬식으로 표현한다.
   

---

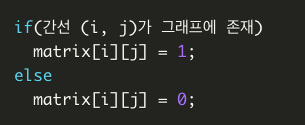
이제 구현 해봅시다

• addNode(node) - 그래프에 노드를 추가합니다.
• addEdge(fromNode, toNode) - fromNode와 toNode 사이의 간선을 추가합니다.
• removeNode(node) - 그래프에서 노드를 삭제합니다.
• removeEdge(fromNode, toNode) - fromNode와 toNode 사이의 간선을 삭제합니다.
• hasEdge(fromNode, toNode) - fromNode와 toNode 사이의 간선 존재 여부를 반환합니다.
• contains(node) - 그래프에 해당 노드가 존재하는지 여부를 반환합니다.

class Graph {
  constructor() {
    /*{"nodes":
	{"1": [], 
	"2": [3], 
	"3": [2]}}
  */
    this.nodes = {};
  }

노드를 추가 합니다.

addNode(node) {// 그래프에 노드 추가
    this.nodes[node] = [];
    //노드가 추가 되면 키와 빈배열 추가  
  }

노드를 확인합니다.

contains(node){
  reutrn this.nodes[node].hasOwnProperty(node);
  //hasOwnProperty는 키있는지 확인하고 t/f리턴
}

노드를 삭제합니다.

removeNode(node){
if(this.nodes[node].length === 0){
	delete this.nodes[node];
  //엣지가 없는 노드라면 노드만 삭제
}else{
	for(let el of this.node[node]){
    	this.removeEdge(node,el);
      //엣지가 있다면 엣지도 순환 하며 엣지도 삭제 
        }
	}
}   

엣지를 추가 합니다.

hasEdge(fromNode,toNode){
for(let el of this.nodes[node]){
	if(el === toNode){
      return ture;
    }
}
  return false;
}

엣지를 추가 합니다.

addEdge(fromNode, toNode) {// fromNode와 toNode 사이의 간선을 추가합니다.
   this.nodes[fromNode].push(toNode);
   this.nodes[toNode].push(fromNode);
  }

엣지를 삭제 합니다.

removeEdge(fromNode, toNode) {//fromNode와 toNode 사이의 간선을 삭제합니다.
    this.nodes[fromNode].splice(this.nodes[fromNode].indexOf(toNode),1);
    this.nodes[toNode].splice(this.nodes[toNode].indexOf(fromNode),1);
  }