4.1 통계적 모형
- 목적: 자료를 이용하여 미지의 관심모수 θ를 추정하는 것
- 통계 추론의 첫 단계: 자료를 생성한 통계적 모형 가정 -> 자료 변수의 확률분포
4.2 우도함수
: f(x|θ). 다양한 θ값에 대해 추정치로서의 가능성을 나타내어 가능도함수(likelihood function)이라고도 함
- x: 이미 관측된 상수
- f(x|θ): θ의 함수 = L(θ) = L(θ|x)
- 우도함수 값이 큰 θ일수록 관측치 x가 주어졌을 때 θ의 참 가능성이 커짐
최우추정치(MLE)
: 우도함수 값을 최대로 만드는 θ값
- logL(θ)는 보통 오목한 모형 -> 이를 미분한 값이 0이 되는 θ가 MLE
우도 원리
: 통계적 실험에서 관측치 x가 가지고 있는 θ의 추론에 대한 정보는 우도함수에 모두 포함되어있음
ex. X|θ ~ B(10,θ)와 X|θ ~ NB(3,θ)
- 고전적 추론: X의 표본공간에 의존 -> 우도함수가 동일하여도 실험방법이 달라 다른 결론 도출
- 베이지안 추론: θ에 대해 같은 사전분포를 가정하면 우도함수가 동일하여 동일한 결론 도출
우도비
: 우도함수의 비율. f(x|θa)/f(x|θb)
충분통계량(Sufficient Statistics)
: X가 밀도함수 f(x|θ)를 갖고, T(X)가 주어졌을 때 X의 조건부 분포가 θ에 의존하지 않는 T(X)
<=> f(x|θ) = g(T(x),θ)h(x) 인 g와 h 존재
- 무수히 많을 수 있음
- 자료 전체도 충분통계량이 될 수 있음
- ex. 평균, 합, (Xi-X.bar)^2의 합, 최댓값
- 최소충분통계량: 가장 잘 요약된, 차원이 가장 작은 통계량
보조통계량(Ancillary Statistics)
: 통계량의 분포가 θ와 무관하여 θ에 대한 정보를 전혀 가지고 있지 않은 통계량
4.3 베이지안 추정
사전분포(prior)
: 자료를 얻기 전 θ에 대한 정보
- 주관적 사전분포 / 객관적 사전분포 or 무정보 사전분포
- 민감성 분석: 다양한 사전분포 때문에 베이지안 추론의 결과가 사전분포에 얼마나 민감하게 변하는지 조사
사후분포(posterior)
: θ에 대한 사전분포 π(θ)와 자료가 주는 θ에 대한 정보 f(x|θ)를 베이즈 정리를 통해 결합한 것
- 충분통계량 T(X)를 알면 간편하게 구할 수 있음
- 베이지안 추정은 사후분포를 근거로 하여 사후기대치 E(θ|x), 사후 중앙값, 최빈값 등을 사용
베이지안 추정 절차
- 사전분포 π(θ) 지정
- 관측치 x를 가지고 적절한 통계 모형으로부터 θ가 주어졌을 때 관측치 x의 조건부 밀도함수 f(x|θ)를 구함
- π(θ)와 f(x|θ)로부터 사후분포 π(θ|x)를 구하고 추정에 사용
4.4 베이지안 구간추정
베이지안 신뢰구간
: 주어진 신뢰수준을 만족하면서 그 구간에 속하는 θ들의 사후밀도함수값이 큰 구간을 찾음
- 사후분포에 근거
- P(θ∈C|x) ≥ 1-α
- 여러개 존재 가능
최대사후구간
: 베이지안 신뢰구간 중에서 구간의 길이가 가장 짧은 구간
조건
θ에 대한 100(1-α)% 최대사후구간:
1. P(θl<θ<θh|x) = 1-α
2. θa∈(θl,θh)이고, θ∉(θl,θh) 이면 P(θa|x) > P(θb|x)
근사적 최대사후구간 구하는 방법
: 최대사후구간을 구하기 위해서 수치적 방법을 사용해야 하는 복잡성 때문에 근사적 HPD 구간 사용을 권장
1. (θ(α/2), θ(1-α/2))를 사용
: α/2 사후분위수, 1-α/2 사후분위수.
- 사후밀도함수가 단봉이 아니거나 비대칭이 심하면 실제와 결과가 달라질 수 있음
2. 격자점 이용
: 연속변수인 θ를 이산변수로 변환
- θ의 모수공간에서 일정한 간격으로 N개의 격자점 θ1,...,θn을 정하고 각 θi에 대하여
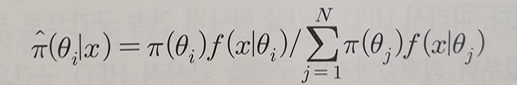 계산
계산 - 위의 값을 내림차순 정렬, 높은 값부터 더해나갈 때 합이 1-α이상이 되는 가장 작은 m을 M이라고 할 때, {θ(1),...θ(M)}이 속하는 구간
- 사후밀도함수의 모양에 상관없이 적용 가능
- 격자점의 수가 크지 않을 경우 근사가 좋지 않을 가능성 있음, θ의 차수가 증가하면서 격자점의 수가 증가, 모수공간이 무한한 경우 격자점 잡기 쉽지 않음
- HPDgrid() 함수 정의
: $index: θ격자점의 첨자, $level: θ 격자점들의 사후확률의 합
# HPDgrid 함수
HPDgrid = function(prob, level=0.95){
prob.sort = sort(prob, decreasing=T)
M = min(which(cumsum(prob.sort)>=level))
height = prob.sort[M]
HPD.index = which(prob>=height)
HPD.level = sum(prob[HPD.index])
res = list(index=HPD.index, level=HPD.level)
return(res)
}
## -0.678 1.278
## 0.9502389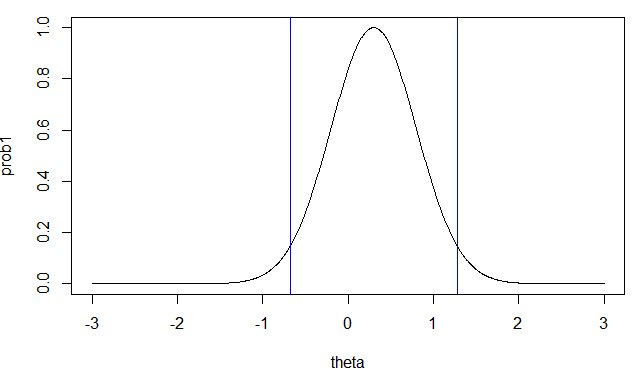
3. 사후 표본 이용
- 사후 표본의 히스토그램이 대략적으로 사후밀도함수와 근사함
- 표본들로 만들 수 있는 CI 구간 중 길이가 가장 짧은 구간을 선택
- θ의 사후밀도함수가 복잡하거나 수리적으로 주어져 있지 않은 경우에도 표본 생성 가능
- 단변량 단봉 밀도함수에 대해서만 적용 가능
- 모수를 임의로 변환해도 변환된 모수의 HPD 구간을 쉽게 구할 수 있음
- HPDsample() 함수 정의
HPDsample = function(prob, level=0.95){
N = length(theta)
theta.sort = sort(theta)
M = ceiling(N*level) # ceiling: x 보다 크거나 같은 정수
nCI = N=M # 가능한 CI의 개수
CI.width = rep(0, nCI)
height = prob.sort[M]
for (i in 1:nCI){
CI.width[i] = theta.sort[i+M] - theta.sort[i]
}
index = which.min(CI.width)
HPD = c(theta.sort[index], theta.sort[index+M])
return(HPD)
}
## -0.6578199 1.2926191베이지안 vs 고전적 추론
베이지안
- θ를 변수로 취급
- 해석이 매우 간단, 직관적
- 신뢰구간에 θ가 속할 확률이 95%
고전적 구간추정
- θ를 상수로 취급
- θ가 구간에 속할 확률은 0 or 1
- 신뢰구간을 구하는 작업을 무수히 반복하면 그 중 95%는 θ를 포함하고 나머지는 포함하지 않을 것
- 현재 우리에게 주어진 신뢰구간이 θ를 포함하는지 아닌지는 알 수 없음
- 해석 복잡
4.5 고정적 추정의 문제점
- 추론의 적합성을 측정하는 측도들은 특정한 관측치에 의존하는 것이 아닌 실험이나 표본조사가 무한히 반복되었을 때 발생하는 모든 가능한 관측치를 고려한 것
- 빈도론자 통계추론(<-> 베이지안은 현재 주어진 관측치에만 의존)
