5.1 이항비율의 추정
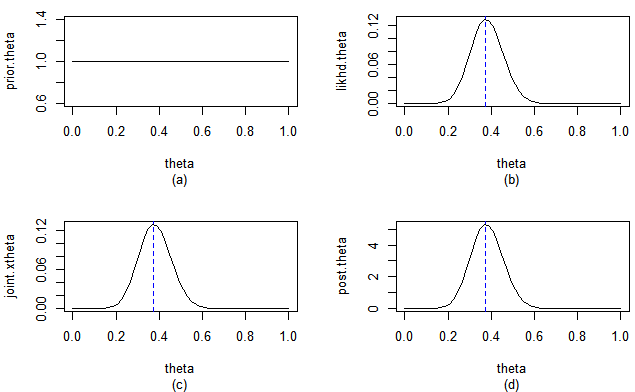
(a) 사전밀도함수 = 상수함수
(b) 우도함수
(c) 우도함수 x prior
(d) posterior = prior x likelihood / f(x1,...xn)
f(x1,...xn): 자료에만 의존하는 θ에 대한 상수함수 => (c)와 y축 스케일만 다를 뿐 형태는 정확히 일치
사전밀도함수와 사후밀도함수의 비교
사전정보는 θ에 대해 차별을 두지 않지만,
사후정보는 자료정보로부터 '40개의 자료 중 15개가 성공이라는 정보'가 추가되어
θ가 0.375에 가까운 값일 확률이 매우 높다는 정보를 줌
몬테칼로 방법
: 사후분포의 밀도함수를 수리적으로 구하기 어려운 경우 사후표본을 생성하여 이 표본을 바탕으로 추정치나 밀도함수를 근사적으로 구할 수 있음
- 표본크기를 더 크게하면 더 정확한 추정 가능
이항분포에서의 로그 오즈의 추정
η = log(θ/(1-θ))
=> η의 표본 생성은 매우 간단: θ의 표본 생성 후 변환
일반적인 경우로의 확장
f(x1,...,xn|θ) = θ^(sum(xi))(1-θ)^(n-sum(xi))
- X = sum(xi))는 θ의 충분통계량 -> 이에 대한 분포만 고려해도 됨
- X1,...,Xn|θ ~ Ber(θ)
X|θ ~ B(n,θ) - 사후분포:
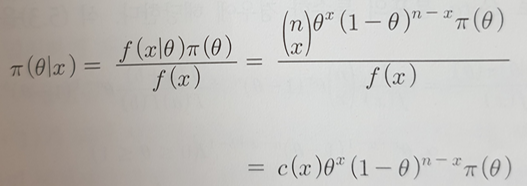
- 이의 적분값이 1이 성립하도록 적분상수 c(x)의 값을 구함
- posterior ∝ prior x likelihood 을 이용할 수도 있음
사전분포: 균일분포
- θ ~ Unif(0,1)
posterior~Beta(x+1, n-x+1) 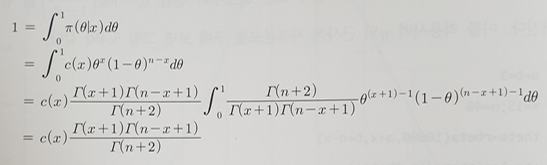
- posterior ∝ prior x likelihood 을 이용하여 posterior이 Beta(a,b) 분포의 밀도함수와 동일한 함수형태이며, 적분값이 1이어야한다는 사실을 이용하여 알아낼 수 있음
- 균일분포는 베타분포의 특수한 경우 Beta(1,1)
- E(θ|x) = (x+1)/(n+2)
사전분포: 베타분포
- θ ~ Beta(a,b)
posterior~Beta(x+a, n-x+b) - E(θ|x) = (a+x)/(a+b+n) = (a+b)/(a+b+n) x 사전평균 + n/(a+b+n) x 표본평균
Var(θ|x) = (a+x)(b+n-x)/(a+b+n+1)(a+b+n)^2 - 사후평균 E(θ|x)는 사전정보와 자료정보의 상대적 정확도를 가중치로 사용한 사전평균과 관측치 평균의 가중평균으로 주어짐
- n이 a+b에 비해 매우 크면 고전적 추정치와 일치
- 고전적 추정치에 비해 베이지안 추정치는 성공과 실패의 관측도수에 양의 상수 a, b를 더하는 효과를 주어 극단적인 값을 추정치로 선택하는 문제 방지 가능
공액 사전분포
: 사전분포와 사후분포가 같은 분포 형태를 가지는 경우
1. 사후분포의 유도가 용이
2. 사후분포가 편리한 형태로 주어져 모테칼로 기법의 적용이 용이
3. 새로운 자료가 추가되었을 때 사후 정보의 개선이 용이
- Beta(a,b) -> 사전분포, 자료 n,x 결합
-> Beta(a+x, b+n-x) -> 자료 수 m, 성공횟수 z
-> Beta(a+x+z, b+n-x+m-z) - 사후분포의 모수만 변경하면 됨(사전 사후분포의 형태가 같으므로)
.
4. 분포의 형태가 고정되어 실제 사전정보를 잘 나타내지 못할 수 있음 => 합성을 통해 해결 가능하지만, 무정보 사전정보를 나타내고자할 때는 문제가 될 수 있음
5.2 예측분포
- 베이지안 추론의 특징: 미래의 관측치에 대한 예측분포를 모수의 추정치에 의존하지 않고 단지 이전의 자료에만 의존하여 구할 수 있음
예측분포
- 일반적으로 베이지안 추론에서는 θ를 변수 취급, 추정치가 θ함수의 가중 평균으로 도출됨
- 추정치의 오차에 θ의 변동성을 적절히 반영
- ex. 5.3
- 조사 결과 40명 중 15명에게 효과가 있었다.
- 고전적 추론: θ.hat = 15/40 = 0.375
예측분포:
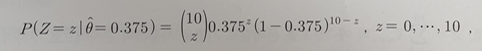
에측평균: 10 x 0.375 = 3.75
예측분산: 10 x 0.375 x 0.625 = 2.3438 - 베이지안 추론:
예측분포: 베타-이항분포
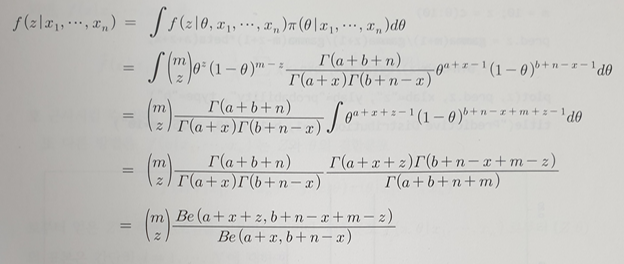
에측평균: 3.8095
예측분산: 2.8558
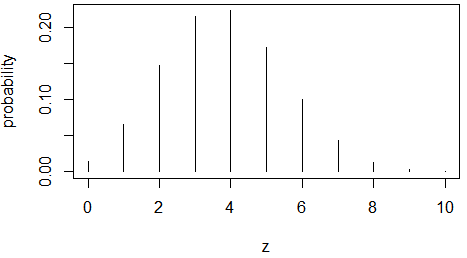
몬테칼로 기법을 사용한 예측분포
- f(z|θ)의 사후평균
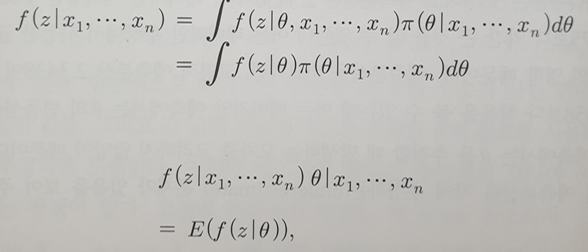
- 근사
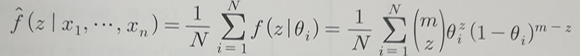
- Z와 θ의 결합분포로부터 얻은 Z의 주변분포임을 이용
θi ~ Beta(a+x, b+n-x)
zi|θi ~ Beta(10, θi)
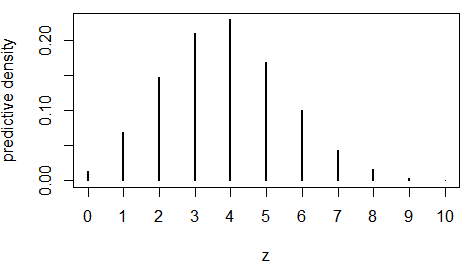
실제 분포와 거의 동일, 예측 기대치, 분산 모두 정확한 근사- 기대치: 3.8127
- 분산: 2.826501
5.3 베이지안 신뢰구간
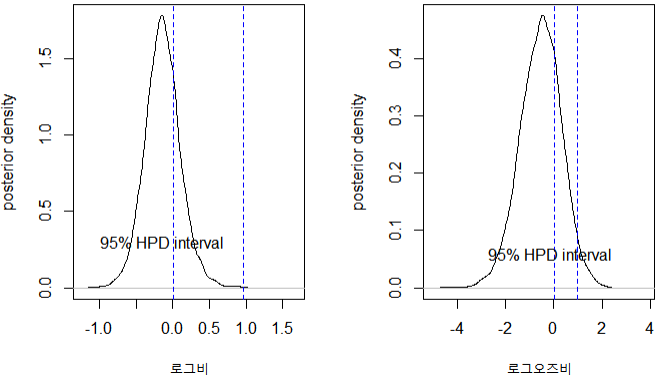
고전적 신뢰구간과 베이지안 최대사후구간
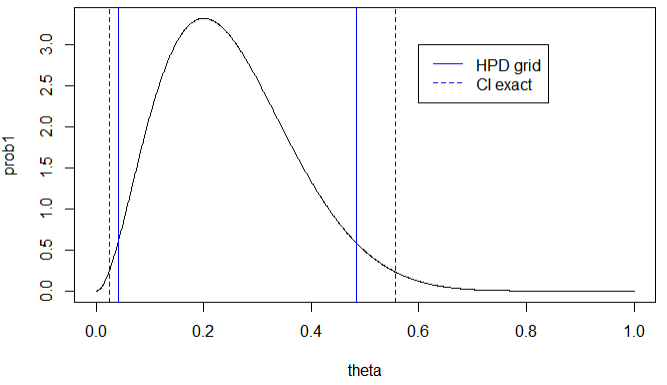
- 최대사후구간이 신뢰구간보다 길이가 짧음
- 균일 사전분포를 사용했을 대, 베이지안 사후분포는 성공과 실패 횟수에 각각 1을 더한 효과를 줌
- θ의 추정치로 변방값인 0, 1을 선택하는 문제를 피할 수 있음
근사적 사후구간과 근사적 신뢰구간
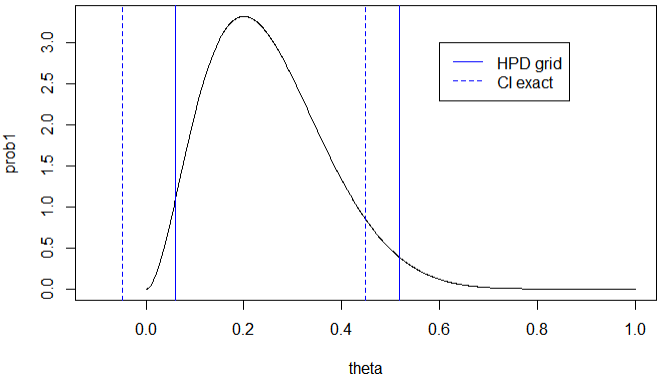
- 표본크기 n이 작을 경우 고전적 추정값 또는 신뢰구간은 적절한 모수 공간을 벗어날 가능성 존재
- 베이지안 추론에서는 사전분포에서 모수를 모수공간으로 제한하면 추정값 또는 신뢰구간이 모수공간을 절대 벗어나지 않음 -> 보다 합리적인 추정 수행 가능
- 위 그림에서 베이지안 신뢰구간이 더 오른쪽에 위치하는 것은 평균이 0.5인 균일 사전분포의 영향 때문
5.4 두 비율의 비교
- 모집단 I의 성공확률: θ1 / 모집단 II의 성공확률: θ2
- θ1 ~ Beta(a1, b1), θ2 ~ Beta(a2, b2)
- θ1|x1 ~ Beta(a1+x1, b1+n1-x1)
θ2|x2 ~ Beta(a2+x2, b2+n2-x2) - 로그비(log ratio): 상대적 비에 로그함수 취함
- 로그함수를 취하면 로그비가 취할 수 있는 값이 전체 실수 공간이 됨
- 비가 1일 때 로그비가 0이 되어 해석 용이
- 로그비: η = log(θ1/θ2)
로그오즈비: ξ = log((θ1/(1-θ1) / θ2/(1-θ2)) - θ1, θ2 사후 표본 추출 -> 표본 변환 -> η, ξ 사후 표본 계산 -> 몬테칼로 방법 이용