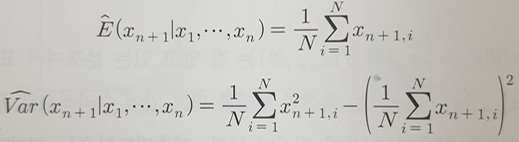[베이지안 통계추론] Chapter 6. 포아송 분포에 대한 베이지안 추론

6.1 포아송 평균의 추정

• θ ~ Gamma(a, b)
  X1,...Xn|θ ~ poi(θ)
  θ|x1,...xn ~ Gamma(a+Σxi, b+n)

• 사전분포는 공액 사전분포: 사후분포의 함수 형태가 동일

• θ의 사후평균: 표본평균의 가중평균
  

  • n이 b에 비해 매우 크면 자료가 사전정보에 비해 많은 정보를 가지고 있다는 것 -> 사후평균이 고전적인 추정치와 일치(=Σxi/n)

• ex. 6.3

  • 사전밀도함수는 균일분포와 다른 모양: 정보를 많이 포함
  • 사전분포는 전체 영역이 아니느, 우도함수가 유의하게 0보다 큰 영역에서만 영향을 미침
    • 사후밀도함수 = 사전밀도함수 x 우도함수
    • (1.5, 3) 구간에서만 사전밀도함수가 사후분포에 영향, 여기서는 균일분포에 가까운 모양
      -> 사전분포는 사후분포에 거의 영향을 미치지 않음
  • 무정보 사전분포: 제프리 사전분포 π(θ) = 1/sqrt(θ)
    • θ|x1,...,xn ~ Gamma(Σxi+1/2, n)
    • 유도된 θ의 사후분포에서 a=1/2, b=0인 경우와 동일

6.2 예측분포

• 예측기대치=사후기대치
  예측분산=사후분산x(b+n+1)

6.3 몬테칼로 근사

• 두 도시의 평균의 차이 η = θ1 - θ2 에 대한 사후추론
  • θ1i|x1 ~ Gamma(a+Σx1j, b+n1)
    θ2i|x2 ~ Gamma(a+Σx2j, b+n2)
    
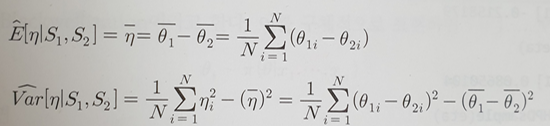
  • 실제 사후기대치 = (a+Σx1j)/(b+n1) - (a+Σx2j)/(b+n2) = -0.2161
    몬테칼로 근삿값 = -0.2157
  • 실제 사후분산 = (a+Σx1j)/(b+n1)^2 - (a+Σx2j)/(b+n2)^2 = 0.0879
    몬테칼로 근삿값 = 0.0875
  • 표본이 커질수록 실제와 근삿값의 차이는 감소함

6.4 예측분포의 몬테칼로 추정

Rao-Blackwellization

• 조건부 기대치 이용
  • 표본 θi를 사후분포로부터 생성한 후, g(θ) = f(x(n+1)|θi)의 평균을 취하면 f(x(n+1)|x1,...,xn)의 추정치를 구할 수 있음

Xn+1 표본 생성하여 예측분포 추정

• θi ~ π(θ|x1,...,xn)
  x(n+1,i)|θi ~ f(x(n+1)|θi)
•