[Python 알고리즘]트리의 지름 구하기 (feat. BOJ 1167)

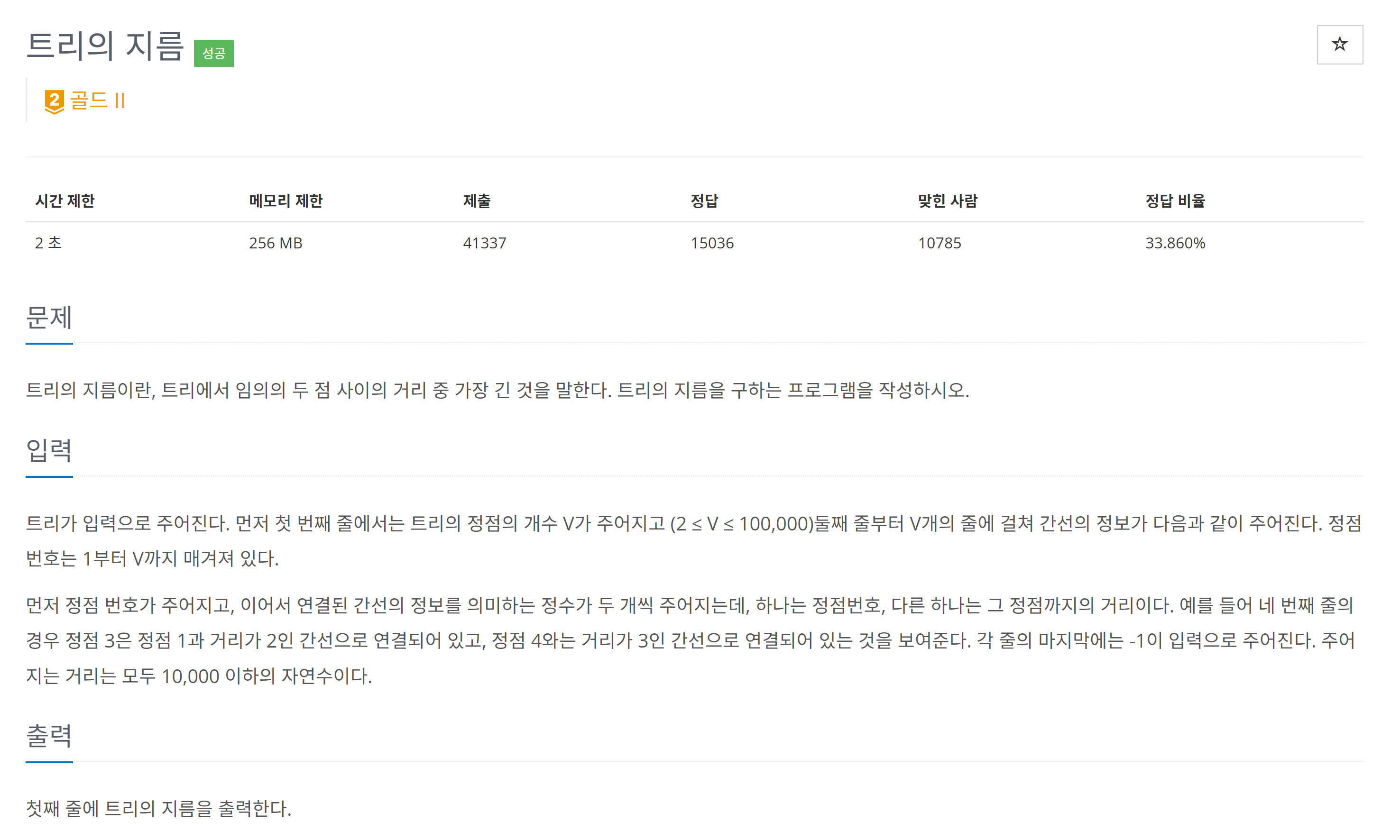
처음 접근했던 방식은 graph와 DFS를 이용한 방법이였다.
distance에 해당 정점에 도착했을 때 가장 먼 거리(distance[i]는 i로 부터 가장 멀리 떨어진 거리)를 저장하도록 하였고, max(distance)를 이용하여 지름을 구하려고 했다.

import sys

input = sys.stdin.readline

# input & init
n = int(input())

graph = [[] for row in range(n + 1)]
distance = [-1 for row in range(n + 1)]
visited = [False for row in range(n + 1)]

for _ in range(n):
    li = list(map(int, input().split()))
    v1 = li[0]
    for i in range(1, len(li) - 1, 2):
        v2, d = li[i], li[i + 1]
        graph[v1].append((v2, d))


# logic
def dfs(now_v, now_d):
    flag = True
    for next_v, next_d in graph[now_v]:
        if not visited[next_v]:
            flag = False
            visited[next_v] = True
            dfs(next_v, now_d + next_d)
            visited[next_v] = False
    if flag:
        distance[now_v] = max(distance[now_v],now_d)
    
    
for i in range(1, n + 1):
    visited[i] = True
    dfs(i, 0)
    visited[i] = False
    
print(max(distance))

시간 초과가 발생하였고, 솔루션을 찾아 보던 중 풀이가 정형화된 문제유형임을 알게되었고 글로 정리해야 겠다고 생각했다.

트리 지름 문제 풀이를 다음과 같이 간단하게 정리할 수 있다.
1. 임의의 한 정점으로부터 가장 먼 거리의 정점을 구한다.
2. 구한 가장 먼 정점으로 부터 가장 먼 거리를 구한다.

문제는 이게 어떻게 지름이라고 확신할 수 있는가이다.
먼저, 그림에서 직관적으로 확인할 수 있는 방법이다.

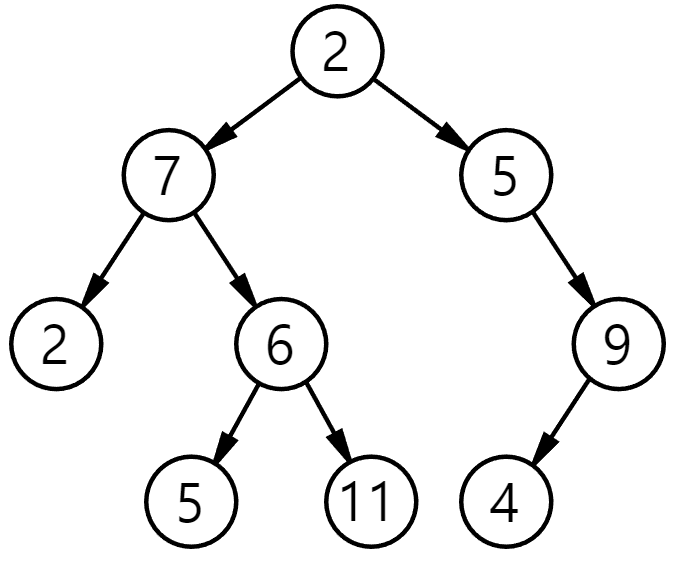
이미지 출처: 위키백과

어떤 정점을 선택했을 때, 가장 먼 거리의 정점은 자식이 없는 노드 중 하나일 것이다. 중간에서 시작했다면 왼쪽 끝이나 오른쪽 끝 노드일 가능성이 크고, 왼쪽 끝 노드에서 시작했다면 오른쪽 끝 노드일 가능성이 클 것이다. 그 정점에서 가장 먼 거리의 정점은 또 오른쪽 끝이나 왼쪽 끝 노드일 가능성이 크고, 저 풀이 방식이 대충 끝점을 먼저 구하고 반대편 끝점을 구하는 방식일 것이라고 직관적으로 이해할 수 있다.

그러나 그림만 가지고서는 엄밀하게 설명할 순 없다. 간선이 서로 다른 가중치를 가지기 때문에 양 끝점이라고 보장할 수 없다.

다음 증명은 https://blog.myungwoo.kr/112를 참고하였다.

트리에서 정점 u와 정점 v 를 연결하는 경로가 트리의 지름이라고 가정하자. 임의의 정점 x를 정하고, 정점 x에서 가장 먼 정점 y를 찾았을 때, 아래와 같이 경우를 나눌 수 있다.

• x가 u 혹은 v인 경우
• y가 u 혹은 v인 경우
• x, y, u, v가 서로 다른 경우

1,2번은 쉽게 생각할 수 있지만, 3번은 다시 경우의 수를 나누어 생각해야 한다.

• x,y 중 한 점이 지름 위에 존재할 때
  이는 x 또는 y가 u 또는 v가 될 것이다.

• x와 y 사이를 경유하는 t가 지름 위에 존재할 때
  지름 위에 존재하는 t에서 가장 먼 거리는 t - u 또는 t - v이다.
  x - t - y 사이 거리가 최대가 되려면 x - t 또는 t - y 사이의 거리가 최대여야 하므로 x - t 가 t - u 또는 t - v이면 된다. (x와 y를 바꿔도 상관없기 때문에 둘 중 하나만 확인하면 된다.) 따라서 t로 부터 두 정점의 길이가 같은 상황을 생각할 수 있고, 지름을 구할 수 있다.

• 정점 x와 정점 y를 연결하는 경로가 정점 u와 정점 v를 연결하는 경로와 완전히 독립인 경우
  x와 y사이를 경유하는 한 점 a와, u와 v사이를 경유하는 한 점 b가 이어져 있는 그림을 생각할 수 있다.
  한 점 a에서 가장 먼 거리는 x - a 혹은 a - y일 것이고 x - a 라고할 때, a - b - u나 a - b - v보다 x - a 가 더 크다. 그렇다면 b에서 가장 먼 거리는 b - u나 b - v가 아닌 b - a - x일 것이다.
  이는 u에서 제일 먼 점이 v가 아니라 x혹은 y가 되어 u와 v를 연결하는 경로가 트리의 지름이 된다는 가정에 모순된다.

다음과 같이 위 풀이에 대한 검증을 마쳤으므로 코드로 작성하면 다음과 같다.

import sys
input = sys.stdin.readline

# input & init
n = int(input())

graph = [[] for _ in range(n + 1)]
for _ in range(n):
    li = list(map(int, input().split()))
    v1 = li[0]
    for i in range(1, len(li) - 1, 2):
        v2, d = li[i], li[i + 1]
        graph[v1].append((v2, d))

max_d = 0
far_node = 0


# logic
def dfs(now_v, now_d):
    global max_d
    global far_node
    if max_d < now_d:
        max_d = now_d
        far_node = now_v

    visited[now_v] = True
    for next_v, next_d in graph[now_v]:
        if not visited[next_v]:
            dfs(next_v, next_d + now_d)


visited = [False for _ in range(n + 1)]
dfs(1, 0)
visited = [False for _ in range(n + 1)]
dfs(far_node, 0)

print(max_d)

코드에서 v는 vertex, d는 distance를 의미한다.