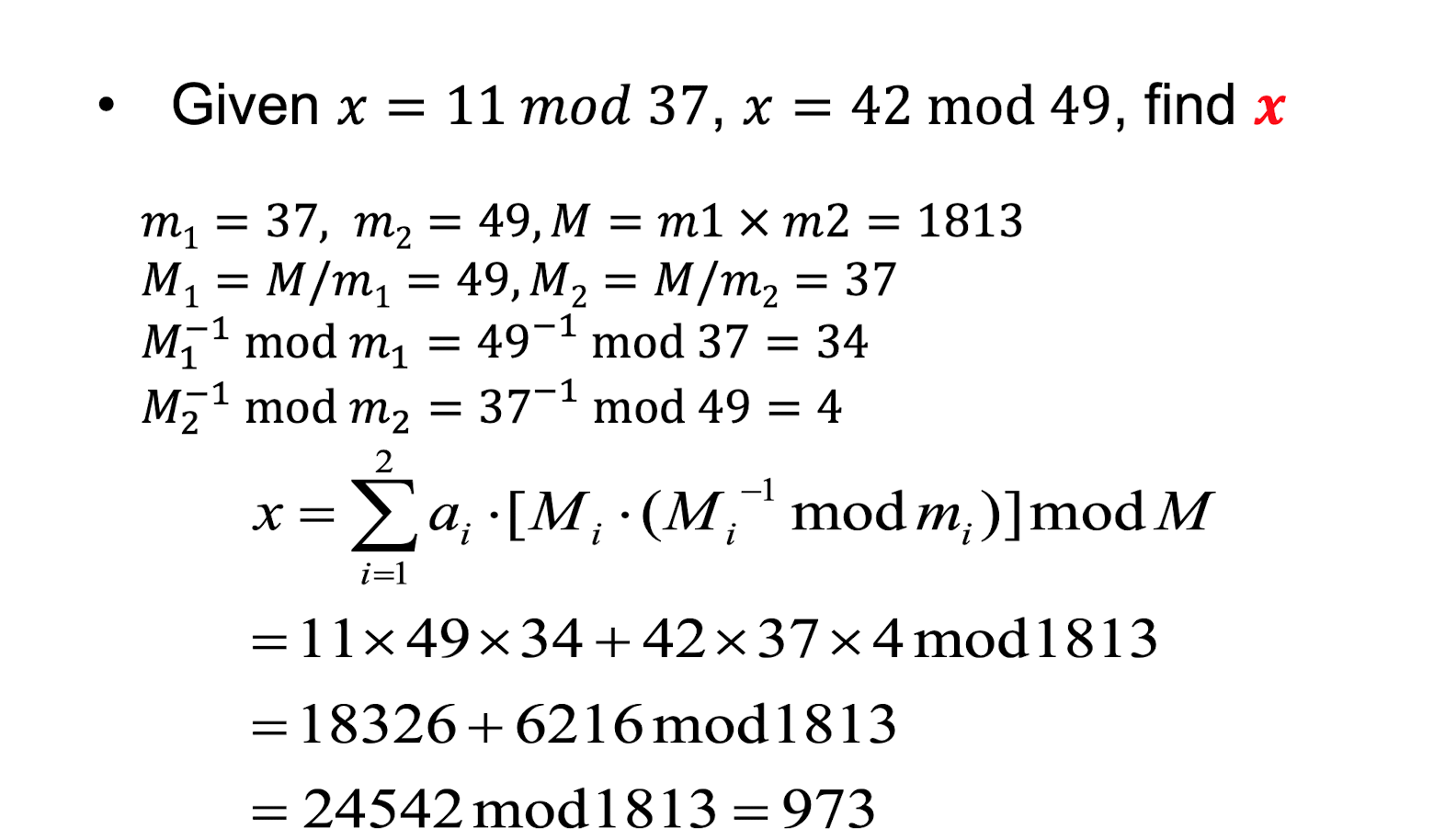Chinese Remainder Theorem (CRT)

거의 설리번선생님의 설명
연립 합동식의 유일한 해를 찾는 정리이다.

정리
$x=\Sigma_1^tx_iD_iM_i$ mod $n$
where $D_i=n/d_i, M_i=D_i^{-1}$ mod $d_i$
연습문제
$d_1=7, d_2=13, x_1=3, x_2=7$라면?
풀이
$n=d_1d_2=7·13=91$
$x_1=3, D_1=91/7=13, M_1=13^{-1}mod7=6$
$x_2=7, D_2=91/13=7, M_2=7^{-1}mod13=2$
$x=(3·13·6+7·7·13)mod91=332mod91=59$

연습문제2

연습문제3

CRT 가 어떻게 RSA의 속도를 올리는가

p=179, q=197
n=35263, $\varphi(n)=34888$
e=17, d=8209 일때
기존 RSA연산
$c = m^e$ mod $n=168^{17}mod35263=28657$
$m=c^d$ mod $n=28657^{8209}$ mod 35263 = 168
이면 굉장히 큰 수 (ex)$28657^{8209}$) 에게 mod계산을 해야해서 느리다.

CRT로 쪼개서 계산하자
$d_p=d$ mod $(p-1)=8209mod178=21$
$d_q=d$ mod $(q-1)=9209mod196=173$
c=28657이면
$c_1=c$ mod $p=28657mod179=17$
$c_2=c$ mod $q=28657mod197=92$
$c_1^{d_p}$ mod $p\equiv16^{21}mod179\equiv168mod179\equiv m$
$c_2^{d_q}$ mod $p\equiv92^{21}mod197\equiv168mod197\equiv m$

Primitive root

정수 a가 있을때 $a^n$(mod p) 의 나머지가 모두 0이 아니라면,
이를 Primitive root라고 부른다.
$a^m = n$ mod $p , for 1<= n < p$

Ex) 3은 Primitive root이다

Elgamal crypt 계산

기본

$Y=g^x$ mod $p$
Y = public key
x = private key (random between 1, p-1)
p = large prime
g = generator (primitive root of $Z^\*\_p$)
(p,g) = public parameters

Encryption

1. (g,x) 사용하여 Y 계산
   $Y=g^x$ mod $p$
2. random으로 k를 골라서 K 계산
   $K=Y^k$ mod $p$
3. M encrypt하여 C(C_1, C_2) 계산
   $C_1=g^x$ mod $p$
   $C_2$ = M X K mod p

Decryption

1. $C_1$, $x$ 사용해서 K 계산
   $C^x_1(\equiv g^kx\equiv Y^k)\equiv$ K mod p
2. $C_2$사용해서 M 복호화
   $M=C_2/K$mod p

Elgamal Examples

Elgamal is >> sementic secure << under Chosen Plain text attack

1. adversary가 $Z^\*\_p$ 에서 $m_b$=($m_0, m_1$)을 고른다.
2. adversary인지 모르고, adversary 에게 $m_b$를 암호화한 C를 리턴한다.
   C = ($C_1=g^x$ mod $p$, $C_2$ = M X K mod p)
3. 똑같은 $m_b$ 암호화시, diffrent k 가 또 diffrent ciphertext를 produce한다. 그러므로 adversary가 같은 ciphertext를 생성하는 것은 불가능하다.
4. 그러므로, adversary는 cannot tell the coreesponding plaintext of C. ($m_b=m_0$ or $m_1$?)
5. as result, ELGamal cryptosystem is semantic secure.

hashing is required!

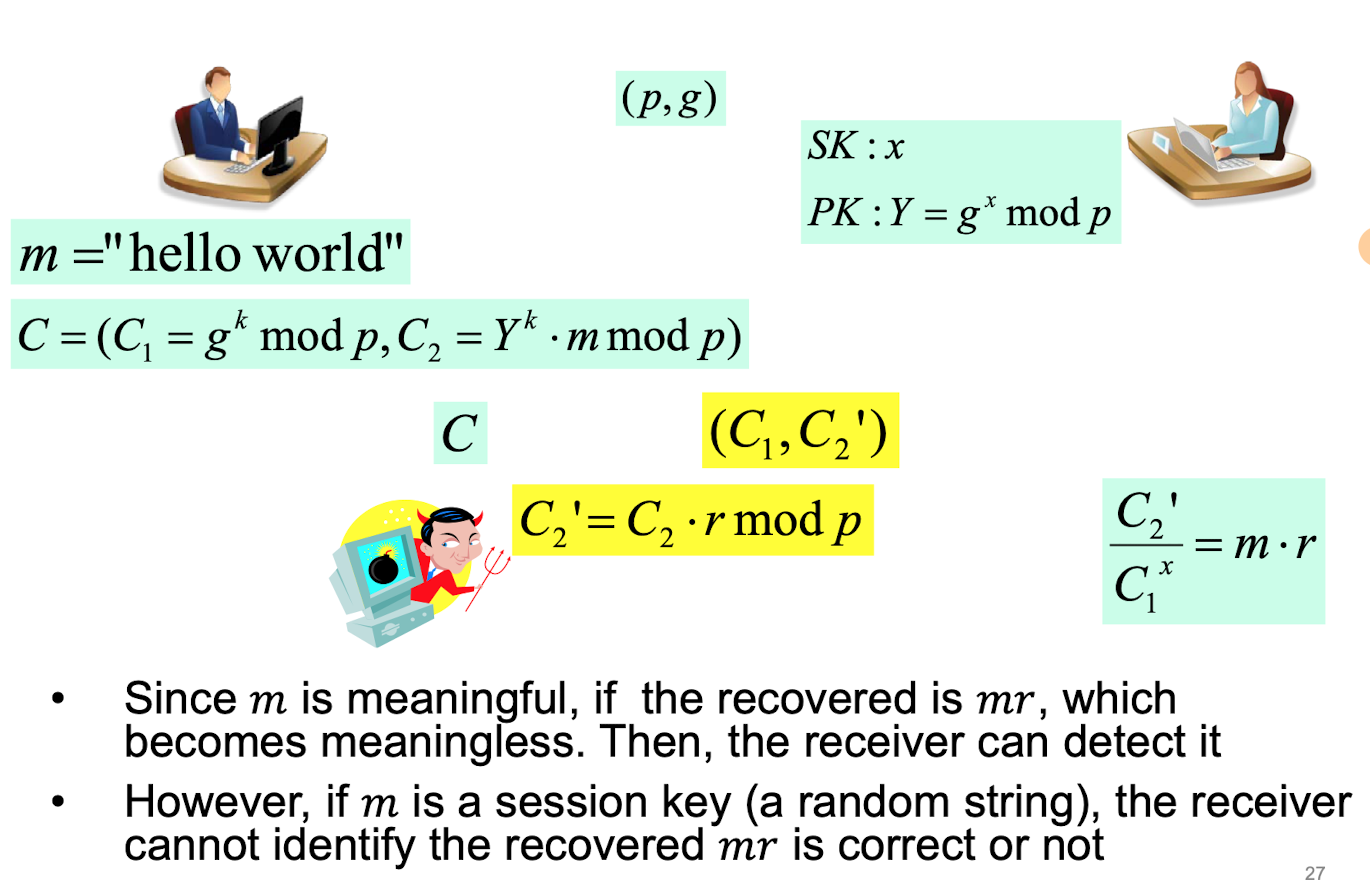
receiver는 C가 조작되었는지, 모를 수 있다. -> 해싱 필요!

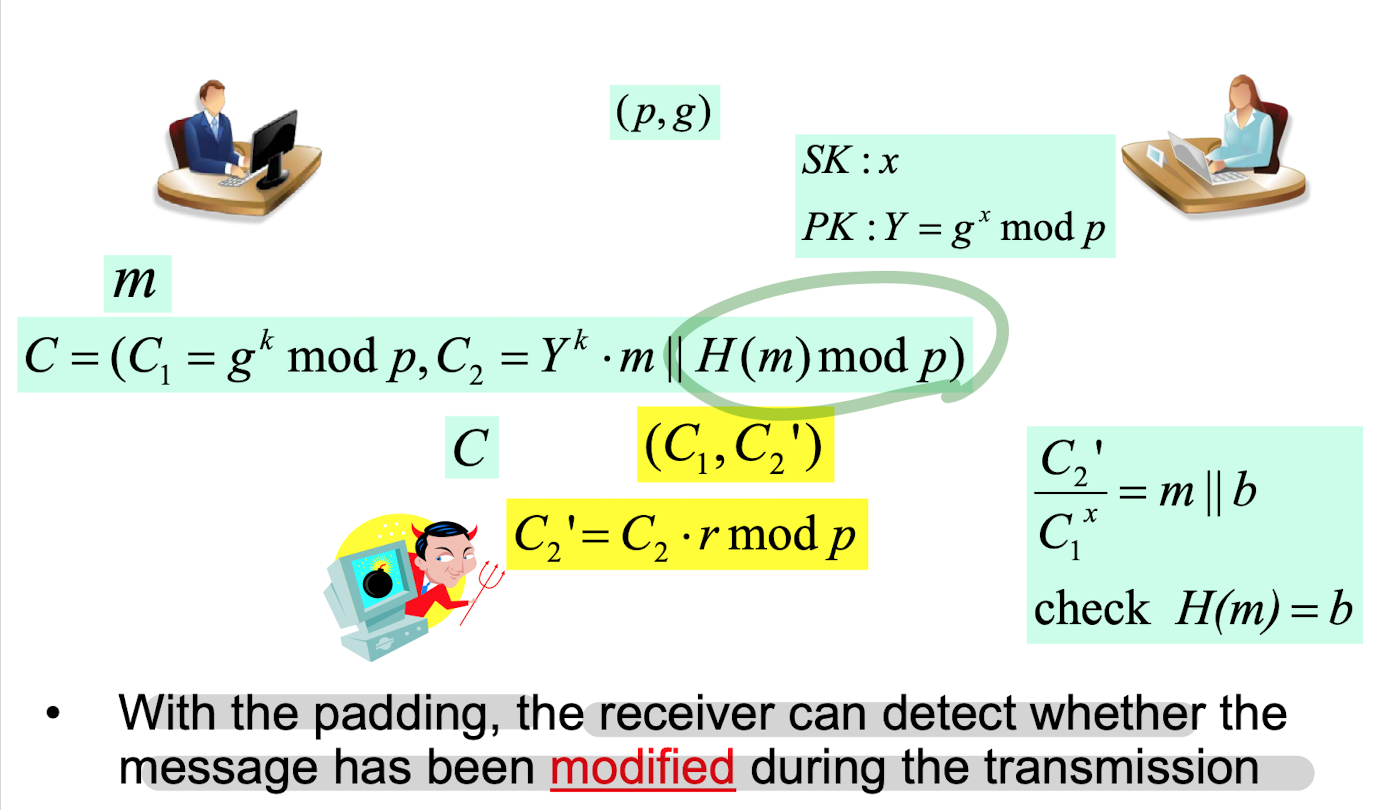
$C_2$에 해쉬패딩을 붙임으로서, receiver는 modifed되었는지, detect 가능
C 전달시, $C_2=Y^k·m||H(m)$ mod $p$ 로 전달

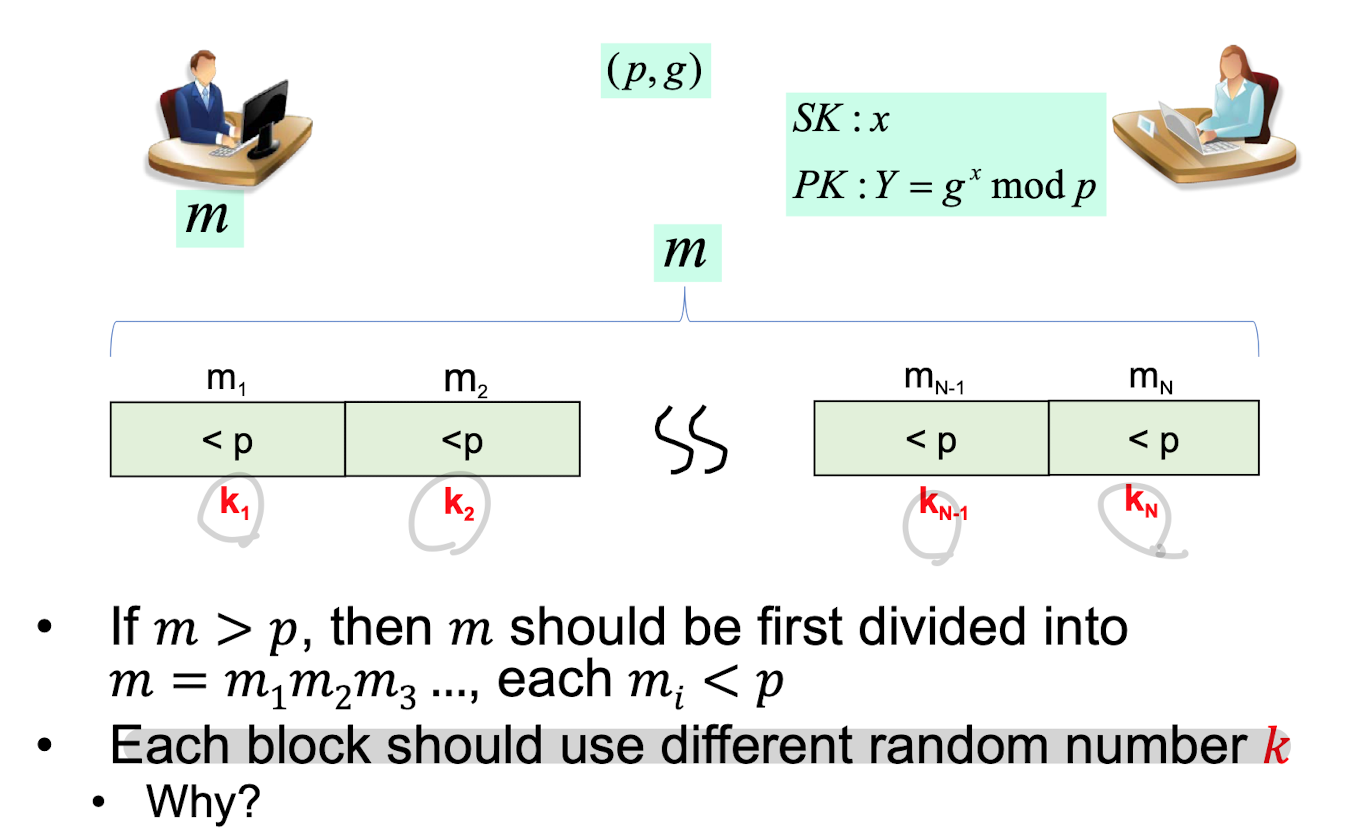
for long message

만약 Block으로 Split시, 매번 다른 K를 choose해야!!

Elgamal Digital Signature

변수

• private key : x
• public key : y = $g^x$ mod $p$

Signing
1. random k를 골라서, r 계산
r = $g^x$ mod $p$
2. m 계산
$m=xr+ks$ mod $(p-1)$
(x를 모르고는, s를 계산해내기 힘들다)
3. signature = (r,s)

Verification
1. receive한 것 = m, r, s
2. signature 체크한다.
$g^m=y^rr^s$ mod $p$ 인지.

• $g^m=y^rr^s$ mod $p$ 과정
  $y^rr^s$ mod $p$
  $=g^{xr}·g^{ks}$ mod $p$
  $=g^{xr+ks}$ mod $p$
  $=g^m$ mod $p$

possible attack

Elgamal Digital Signature + HASH

변수

• private key : x
• public key : y = $g^x$ mod $p$

Signing
1. random k를 골라서, r 계산
r = $g^x$ mod $p$
2. m 계산하고 Hash씌우기
$m=xr+ks$ mod $(p-1)$
(x를 모르고는, s를 계산해내기 힘들다)
$H(m)$
3. signature = (r,s)

Verification
1. receive한 것 = m, r, s
2. m에 Hash 씌우기
m -> H(m)
3. signature 체크한다.
$g^{H(m)}=y^rr^s$ mod $p$ 인지.