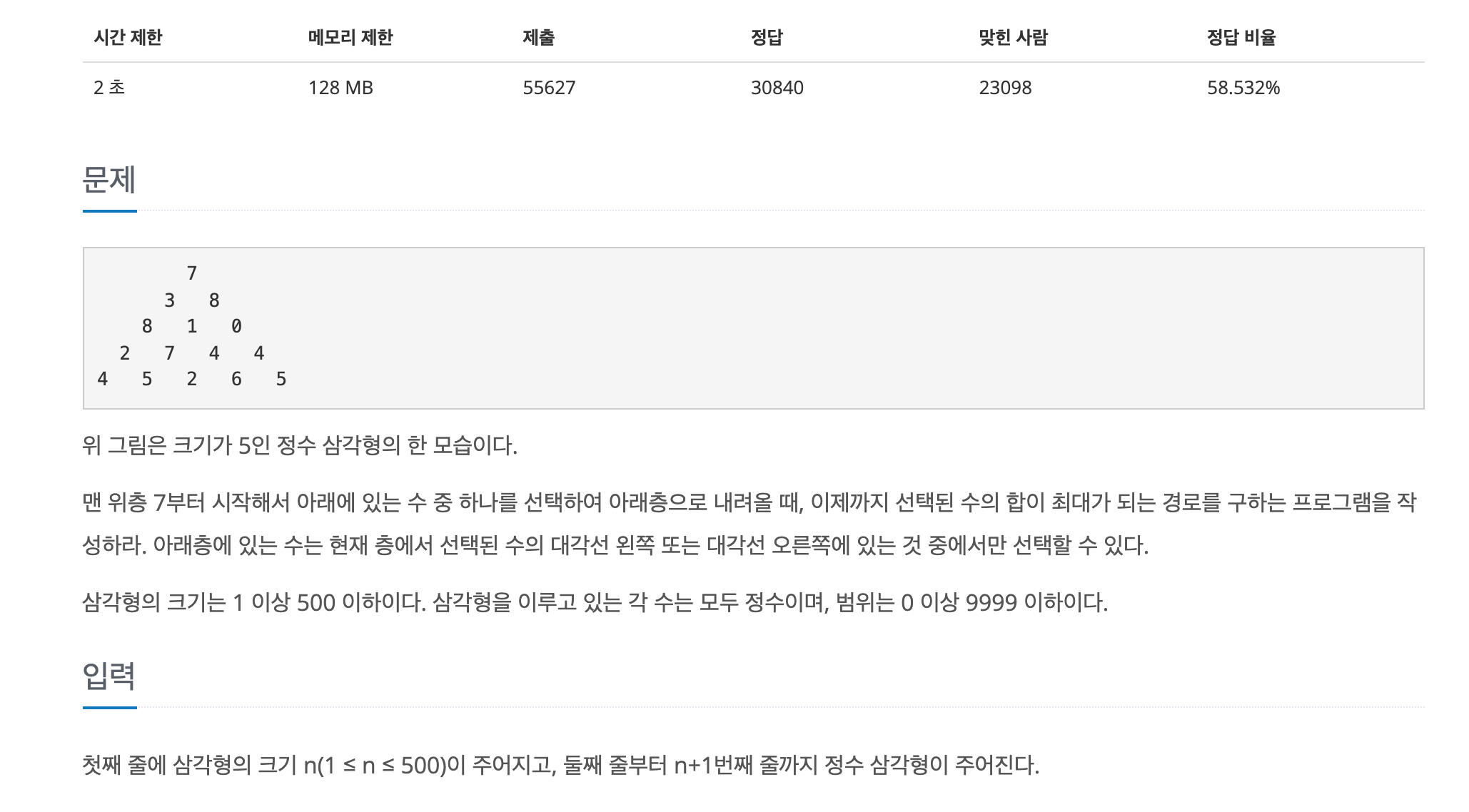
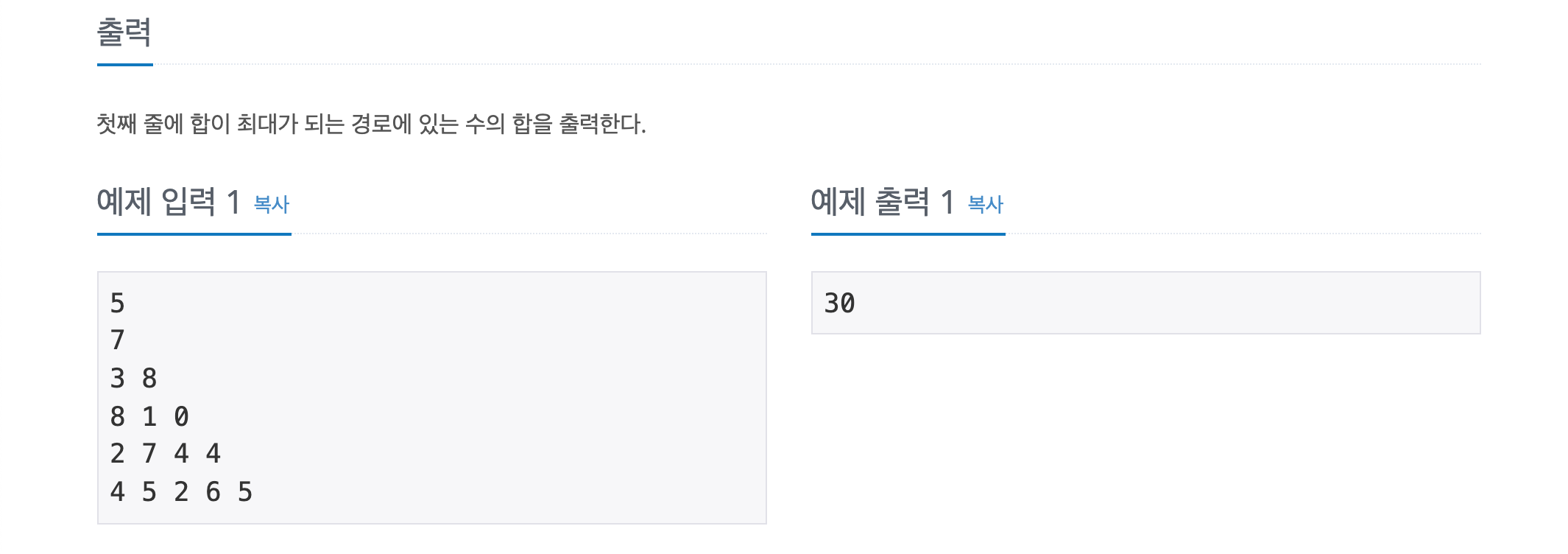
문제

백준1932번정수삼각형

풀이

풀이 아이디어

특정 위치로 도달하기 위해서 '왼쪽위' 혹은 '바로 위' 2가지 위치에서만 내려올 수 있다.
따라서, 모든 위치를 기준으로 이전 위치로 가능한 2가지 위치까지의 최적의 합 중 더 큰 합을 가지는 경우 선택
$dp[i][j]=array[i][j]+max(dp[i-1][j-1], dp[i-1][j])$

• 주의사항
  • 접근할때마다 리스트의 범위 벗어나지 않는지 체크
  • 구현 편의상 array 따로 사용하지 않고, Dp 테이블에 초기 데이터 담아서 점화식에 따라 dp 테이블 갱신

느낀점

• dynamic 과 greedy가 큰 차이가 무엇인지 뚜렷하게 설명 못하겠다
  • 이 벨로그를 읽고 다시 이해
• 어떻게 저 점화식이 최적을 보장하는지 직관적으로 이해가 안됨
  • 모든 경우를 탐색하되, 겹치는 경우를 대체하는 것으로 이해하자 (유남생..? 피보나치로 생각하세요)

풀이

n = int(input())
dp = [] #다이나믹 프로그래밍을 위한 DP 테이블 초기화

for _ in range(n):
	dp.append(list(map(int, input().split())))

# 다이나믹 프로그래밍으로 두 번째 줄 부터 내려가면서 확인
for i in range(1, n) :
	for j in range(i+1):
		# 왼쪽 위에서 내려오는 경우
		if j == 0 :
			up_left = 0 # 범위에서 벗어남
		else :
			up_left = dp[i-1][j-1]  # 값 저장
		# 바로 위에서 내려오는 경우
		if j == i :
			up = 0 # 범위에서 벗어남
		else :
			up = dp[i-1][j] # 값 저장
		# 최대 합으로 저장
		dp[i][j] = dp[i][j] + max(up_left, up)

print(max(dp[n-1]))

이해를 위한 출력용 코드