예제) 음료수 얼려먹기
이코테 149p
문제
-
제한
- 1초 / 128MB
-
입력
- 얼음틀 세로길이 N, M (1<=N, M<=1,000)
- 2줄~N+1줄까지 얼음틀 형태 주어짐 (0=구멍, 1=그렇지 않음)
-
출력
- 한번에 만들 수 있는 아이스크림의 갯수 출력
-
예시
N * M 크기의 얼음 틀이 있다.
구멍이 뚫린 부분은 0, 칸막이가 있는 부분은 이다.
00110
00011
11111
00000
일 경우 아이스크림이 3개 생성된다.
해결책 찾는 방식
- 행렬형태를 그래프로 바꾸어 생각하자.
- pytohnic한 상하좌우 움직이는 법에 익숙해지자
- 연결되어있는 덩어리 찾는 방법 = DFS/BFS로 연결된 부분'만' 전부 탐색하기
를 생각해내기
-
개인적으로는 DFS/BFS = 찾는 '탐색' 으로만 집중했는데
탐색이 가능한 조건은 '그래프(덩어리)'안에서 '연결되어있는 경로로만' 탐색이 가능하다는 점을 캐치하고 나서 왜 DFS/BFS가 쓰여야하는지를 인지하게 됐다. -
'어떻게 덩어리를 찾을 수 있지?' -> '덩어리 = 한개의 그래프'일때, DFS/BFS를 통해 모든 연결된 node를 탐색하여 덩어리를 구분 할 수 있겠군
의 생각의 흐름이 바람직할 것 같다.
해결책
- 특정 지점의 주변 상,하,좌,우 를 살펴본 뒤에, 주변 지접 중에서 값이 0이면서 아직 방문하지 않은 지점이 있다면 해당 지점을 방문한다.
- 방문한 지점에서 다시 상,하,좌,우를 살펴보면서 방문을 다시 진행하면 연결된 모든 지점을 방문할 수 있다.
- 1~2과정을 모든 노드에 반복하며 방문하지 않은 지점의 수를 센다.
코드
n, m = map(int, input().split())
graph = []
for i in range (n) :
graph.append(list(map(int, input())))
# DFS
def DFS(x, y) :
stack = []
# 주어진 범위를 벗어나는 경우 즉시 종료
if x <= -1 or x >= n or y <= -1 or y >= m :
return False
# 현재 노드를 아직 방문하지 않았다면
if graph[x][y] == 0 :
# 해당 노드 방문 처리
# 상 하 좌 우 위치도 모두 재귀적으로 호출
dfs(x-1, y)
dfs(x, y-1)
dfs(x+1, y)
dfs(x, y+1)
return True
return False
# 모든 노드에 대하여 음료수 채우기
result = 0
for i in range(n) :
for j in range(m) :
# 현재 위치에서 DFS 수행
if DFS(i, j) == True :
result += 1
print(result)
기억했으면 좋겠따
- 체스판에서 움직이는법
- 기존 DFS에서는 연결된 모든 node에게(리스트 활용) 재귀적으로 dfs()를 호출했는데
- 2*2 테이블을 기준에서 하자니 4방향으로 dfs()를 일일히 호출하도록 기존 dfs를 살짝 변형하여 푸는게 인상깊다.
- 거의 정석처럼 쓰이는 방식이니 익숙해지자
예제) 미로탈출
이코테 152p
문제
- 제한
- 시간 1초 / 메모리 128MB
- 입력
- 정수 N, M (4<=N, M<=200)
- N개 줄에 0또는 1의 M개의 정수로 미로 정보 주어짐
- 출력
- 최소 이동칸의 갯수 출력
- 상황
- N*M 미로에 갇혀있다.
(1,1)에서 출발하여 출구 (N,M)에 가야한다. - 0을 피해 1로만 움직일 수 있다.
- 탈출하기 위해 움직여야하는 최소 칸의 갯수를 구하시오
- N*M 미로에 갇혀있다.
(풀이) 왜 BFS가 적용되어야하는가
- 시작지점부터 가까운 노드부터 차례로 모든 노드를 탐색한다.
= "가까운" 노드부터 탐색하는 것이므로, 처음으로 조건을 만족하는 때가 "최소" 임을 보장할 수 있다!
위의 DFS와 마찬가지로,
BFS는 탐색알고리즘인데 왜 여기에 적용되어야하는가를 생각할 수 있어야한다!
BFS의 특징(이자 구현자체)에서
BFS에서 처음으로 조건을 만족하는 때가, '최소' 임을 보장함을 추론해낼 수 있었으면 좋겠다!
벽은 0이고, 갈 수 있는 길은 1일때, BFS 수행할때마다 ++ 해주면, 최종 목적지에는 지금까지 움직인 수가 기록된다.
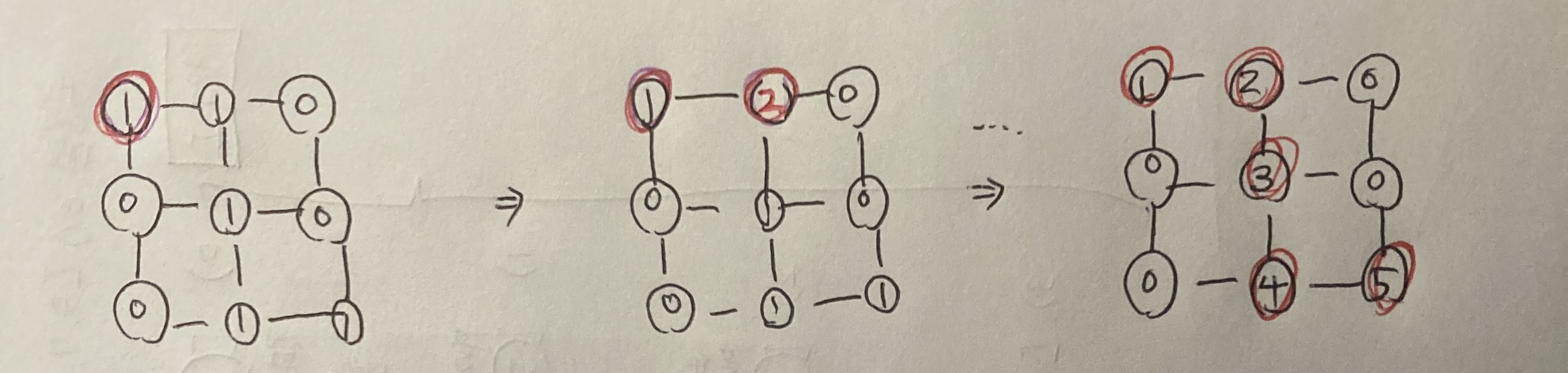
밑의 코드를 보고, 어떻게 카운트 되는지 인지하자!
- 이렇게 카운트하면, <0이면 벽이어서 못가고, 2면 이미 방문해서 못간다>로 큐에 꺼낸 지점을 방문할지 말지 결정할 수 있다.
(풀이) 그 외
- 2차원 리스트 형태를 그래프로 생각해내는 법
- 4방으로 움직이는 걸 dx, dy (갈 수도 있는 좌표)를 활용하여 구현하는 법
코드
from collections import deque
# N, M 공백으로 구분하여 입력받기
n, m = map(int, input().split())
# 2차원 리스트의 맵 정보 입력받기
graph = []
for i in range (n) :
graph.append(list(map(int, input())))
# 이동할 네 방향 정의
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
# BFS 코드 구현
def bfs(x,y) :
# queue 구현을 위해 deque라이브러리 사용
queue = deque()
queue.append((x,y))
# queue가 빌때까지 반복
while queue :
x, y = queue.popleft()
# 현재 위치에서 네 방향으로의 위치 확인
for i in range(4) :
# nx,ny = 갈수도 있는 좌표
nx = x + dx[i]
ny = y + dy[i]
# 미로 찾기 공간을 벗어난 경우 무시
if nx<0 or ny<0 or nx>=n or ny>=m :
continue
# 벽인 경우 무시
if graph[nx][ny] == 0 :
continue
# 해당 노드를 처음 방문하는 경우에만 최단 거리 기록
####################################
# 0이면 벽이어서 못가고, 2면 이미 방문해서 못간다.
if graph[nx][ny] == 1 :
##########################
graph[nx][ny] = graph[x][y] + 1 #1을 더해서, 지금까지 온 만큼을 카운트 한다!!
#########################
queue.append((nx, ny)) # nx, ny가 진짜 가는 좌표가 된다.
# 가장 오른쪽 아래까지의 최단거리 반환
return graph[n-1][m-1]
