그래프(Graph)

그래프

그래프

• 자료구조의 일종
• 정점(Node, Vertex)
• 간선(Edge): 정점간의 관계를 나타낸다.
• G = (V, E)로 나타낸다.

경로(Path)

• 정점 A에서 B로 가는 경로

사이클

• 정점 A에서 다시 A로 돌아오는 경로

단순 경로와 단순 사이클(Simple path and Simple Cycle)

• 경로/사이클에서 같은 정점을 두 번 이상을 방문하지 않는 경로 사이클
• 특별한 말이 없으면, 일반적으로 사용하는 경로와 사이클은 단순 경로/사이클

방향 있는 그래프

• A->C와 같이 간선에 방향이 있다.

방향 없는 그래프

• A-C와 같이 간선에 방향이 없다.
• A-C는 A->C C->A를 나타낸다.
• 양방향 그래프(Bidirectional Graph)라고도 한다.
• 방향 없는 그래프는 나중에 다 방향 있는 그래프로 바꾸어 저장!

간선 여러개

• 두 정점 사이에 간선이 여러 개일 수도 있다.
• A->B를 향하는 간선이 여러 개인 경우.

루프

• 간선 양 끝 점이 같은 경우

가중치

• 간선에 가중치가 있는 경우에는
• A에서 B로 이동하는 거리, 이동하는 데에 필요한 시간, 이동하는 데에 필요한 비용 등등등...

차수(Degree)

• 정점과 연결되어 있는 간선의 개수
• 방향 그래프의 경우에는 In-degree와 Out-degree로 나누어서 차수를 계산한다.

그래프의 표현

• 아래와 같은 그래프는 정점이 6개, 간선이 8개 있다.
• 간선에 방향이 없기 때문에, 방향이 없는 그래프이다.
• 정점: {1, 2, 3, 4, 5, 6}
• 간선: {(1, 2), (1, 5), (2, 5), (2, 3), (2, 4), (3, 4), (4, 5), (4, 6)}
  
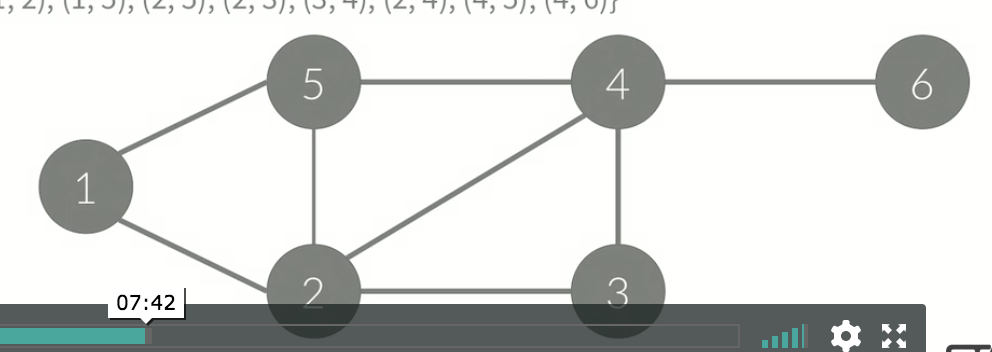
  <출처 백준 알고리즘기초 2>

그래프 저장 방법

• 인접 행렬
• 인접 리스트
• 한 정점 x와 연결된 간선을 효율적으로 찾는 구조를 만들기 위해 그래프 저장 방법 2 가지를 배움.

인접 행렬(Adjacency Matrix)

• 정점의 개수를 V라고 했을 때

• VxV 크기의 이차원 배열을 이용한다.

• A[i][j]=1(i->j 간선이 있을 때), A[i][j]=0 (없을 때)

• A[i][j]=w(i->j 간선이 있을 때, 그 가중치 w), A[i][j]=0 (없을 때)

• 정점 V개, 간선 E일 때,

  • 공간: V^2
  • 한 정점에 연결된 모든 간선을 찾는 시간 복잡도: O(V)

인접 리스트(Adjacency List)

• 리스트를 이용해서 구현한다
  • 간선이 몇 개가 있을 지 알 수 없는 경우에 사용.
  • 동적으로 하나씩 증가시켜 사용
• A[i]=i와 연결된 정점을 리스트로 포함하고 있음.
• 가중치가 있을 경우, 해당 정점 번호와 가중치를 묶어서 저장해줌.

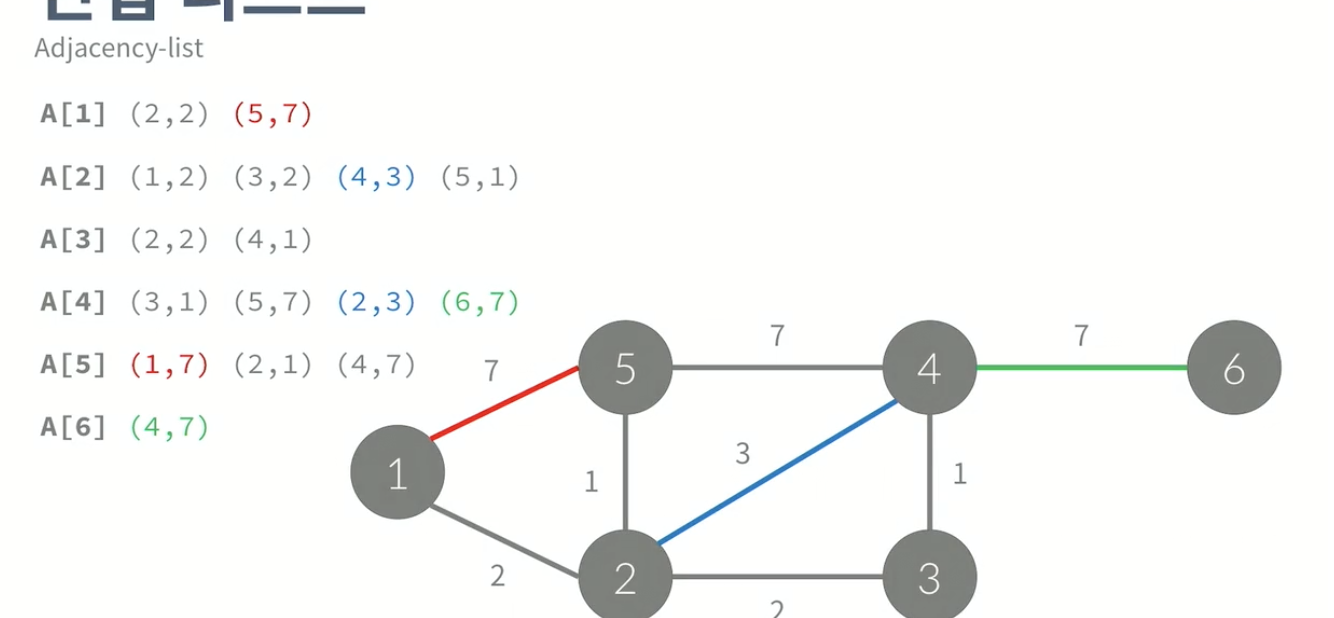
<출처 백준 알고리즘기초2>

• 리스트는 크기를 동적으로 변경할 수 있어야 한다.
• 링크드 리스트나 길이를 동적으로 변경할 수 있는 배열(vector)을 사용한다
  • 링크드 리스트 없이 C++의 vector을 사용하면 됨!
• 공간 복잡도:
  • 인접 행렬: O(V^2)
  • 인접 리스트: O(E) -> 없는 간선은 저장하지 않기 때문
• 시간 복잡도:
  • 인접 리스트-한 정점과 연결된 모든 간선을 찾는 시간: O(차수)
• 공간적, 시간적으로 인접 리스트가 유리하기에, 우리는 인접 리스트 를 사용해서 구현할 것!
• 임의의 두 정점 사이에 간선이 있는지/없는지 구할 때, 시간적으로 인접 행렬이 더 유리함.

간선 리스트(Edge List)

• 배열을 이용해서 구현한다.
• 간선을 모두 저장하고 있다.
• E라는 배열에 간선을 모두 저장한 후, 앞 정점을 기준으로 정렬하여 cnt라는 배열에 넣어줌
  
  <출처 백준 알고리즘기초2>

i	0	1	2	3	4	5	6
cnt[i]	0	2	6	8	12	15	16

• 1번은 0부터 2 전 까지, 2번은 2부터 6 전까지, ...
• 시간복잡도: O(차수) + 정렬
• 인접리스트는 써야하는데, 라이브러리의 사용이 금지되어 있어서, 링크드리스트를 구현하자니 머리가 아플 때 사용하는 것!

그래프의 탐색

• DFS: 깊이 우선 탐색 --> stack
• BFS: 너비 우선 탐색 --> queue
• 목적: 임의의 정점에서 시작해서 연결되어 있는 모든 정점을 1번씩 방문하는 것.
• 차이: 어떤 순서로 정점을 방문할 것이냐=

깊이 우선 탐색

• 스택을 이용해서 갈 수 있는 만큼 최대한 많이 가고
• 갈 수 없으면 이전 정점으로 돌아간다.
• 정점을 방문했는지 체크하는 check 배열 생성(1이면 방문, 0이면 미방문), 스택을 사용
• 재귀 호출을 이용해서 구현할 수 있다.

//x를 방문
//시간복잡도 O(v^2)
void dfs(int x){
  check[x]=true;
  //n=v
  for(int i=1; i<=n; i++){
    if(a[x][i]==1&&check[i]==false){
      dfs(i);
    }
  }
}

• 인접리스트를 이용해서도 구현할 수 있다.

//시간 복잡도O(V+E)
//대부분 v<=e이기 때문에, O(E)
void dfs(int x){
  check[x]=true;
  for(int i=0; i<a[x].size(); i++){
    int y=a[x][i];
    if(check[y]==false){
      dfs(y);
    }
  }
}

너비 우선 탐색

• 큐를 이용해서 지금 위치에 갈 수 있는 것을 모두 큐에 넣는 방식

• 큐에 넣을 때( 뺄 때가 아니라 넣을 때!!) 방문했다고 체크해야 한다.

• 인접 행렬을 사용하여 구현할 수 있다.

• 1260 문제 풀어보기!

queue<int> q;
check[1] = true;
q.push(1);
while(!q.empty()){
  int x = q.front();
  q.pop();
  for(int i=1; i<=n; i++){
    if(a[x][i]==1&&check[i]==false){
      check[i]=true;
      q.push(i);
    }
  }
}