Algorithm
1.알고리즘 기초
입력의 크기 N에 대해서 시간이 얼마나 걸릴지 나타내는 방법표기법: 대문자 O(Big O Notation)최악의 경우에 시간이 얼마나 걸리는지 나타냄.시간 복잡도는 소스를 보고 계산 할 수도 있고, 소스를 작성하기 전 에 먼저 계산해볼 수 있음.문제를 풀기 전 먼저 생
2.스택(Stack)

한쪽 끝에서만 자료를 넣고(push) 뺄 수 있는(pop) 자료구조.제일 위(top)에 있는 것만 알 수 있음.일차원 배열 하나로 구현할 수 있다.
3.큐(Queue)와 덱(Deque)

한쪽 끝에서만 자료를 넣고 다른 한쪽 끝에서만 뺄 수 있는 자료구조.FIFO 구조자료를 순서대로 처리해야할 때 많이 사용함. 예) BFS일차원 배열 하나로 구현할 수 있음. (begin, end-1)STL의 queue를 사용하는 것을 추천.양 끝에서만 자료를 넣고 양
4.수학

(A+B) mod M = ((A mod M) + B mod M) mod M(AB) mod M = ((a mod M) (B mod M)) mod M뺄셈의 경우에는 먼저 mod 연산을 한 결과가 음수로 나올 수 있기 때문에 다음과 같이 해야한다.(A-B) mod M =
5.다이나믹 프로그래밍(Dynamic Programming)

큰 문제를 작은 문제로 나눠서 푸는 알고리즘두 가지 속성을 만족해야 다이나믹 프로그래밍으로 문제를 풀 수 있다.Overlapping Subproblem(겹치는 부분/작은 문제)Optimal Substructure(최적 부분 구조)다이나믹 프로그래밍작은 문제가 중복이 되
6.브루트 포스(Brute Force)

브로트 포스는 모든 경우의 수를 다 해보는 것브루트 포스로 문제를 풀기 위해서는 다음과 같은 3가지 단계를 생각해볼 수 있음.문제의 가능한 경우의 수를 계산직접 계산을 통해 구함. 대부분 손으로 계산해볼 수 있다.가능한 모든 방법을 다 만들어 봄하나도 빠짐 없이 만들어
7.그래프(Graph)
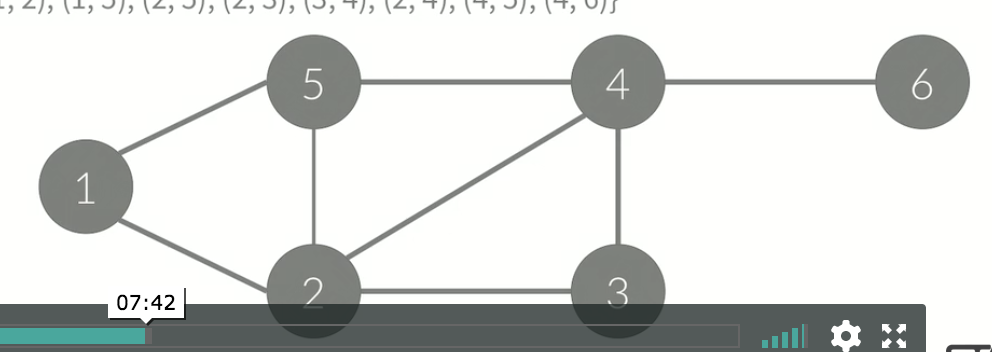
자료구조의 일종정점(Node, Vertex)간선(Edge): 정점간의 관계를 나타낸다.G = (V, E)로 나타낸다.정점 A에서 B로 가는 경로정점 A에서 다시 A로 돌아오는 경로경로/사이클에서 같은 정점을 두 번 이상을 방문하지 않는 경로 사이클특별한 말이 없으면,
8.연결 요소(Connected Component)

그래프가 아래 그림과 같이 나누어져 있지 않은 경우가 있을 수도 있다.아래 그래프는 그래프가 하나일 수도, 두 개일 수도 있다.아래 그래프를 하나라고 했을 때, 연결 요소가 2개가 있는 그래프라 볼 수 있다.연결 요소가 2개 이상이면, 그래프가 끊어져있는 것.이렇게 나
9.트리(Tree)

자료 구조의 일종사이클이 없는 연결 그래프정점의 개수: V, 간선의 개수: V-1정점 N개 간선 N개일 때에는 사이클이 1개 있음루트가 있는 트리루트부터 아래로 방향을 정할 수 있다깊이(Level): 루트에서부터 트리(루트의 깊이를 0으로 하는 경우와, 1로 하는 경우
10.[자료구조] 탐색

맵(map) 또는 사전(dictionary)은 자료를 저장하고 키를 이용해 원하는 자료를 빠르게 찾을 수 있도록 하는 자료구조키를 가진 레코드(keyed record) 또는 엔트리(entry)라 불리는 키-값 쌍(key, value)을 테이블에 저장한다이때 각 키는 유
11.[자료구조] 배열을 이용한 탐색

정렬되지 않은 배열을 이용하는 방법(2. 정렬된 배열을 이용하는 방법(3. 이진 탐색 트리를 이용하는 방법해싱을 이용하는 방법순차탐색(Sequential Search)가장 간단하고 직접적인 탐색 방법배열의 요소들을 처음부터 마지막까지 하나씩 검사하여 원하는 레코드를 찾
12.[프로그래머스] 폰켓몬(Hash) 문제 풀이(Python)

내가 푼 문제 풀이dict 사용 대신 set() 사용중복되는 번호를 체크하기 위해서 type_dict라는 dict()를 사용했다.그리고 중복이 될 때마다 value에 1씩 더해주면서 중복되었음을 활용했다.하지만, 만약 set()함수를 썼다면 이와 같은 연산이 불필요했을
13.[프로그래머스] K번째수(정렬) 문제 풀이(Python)

람다를 활용하면 좋을 것
14.[프로그래머스] 더 맵게(heap) 파이썬

참고 gmlwjd9405 github