1. 회귀(Regression)
선형회귀
단순선형회귀
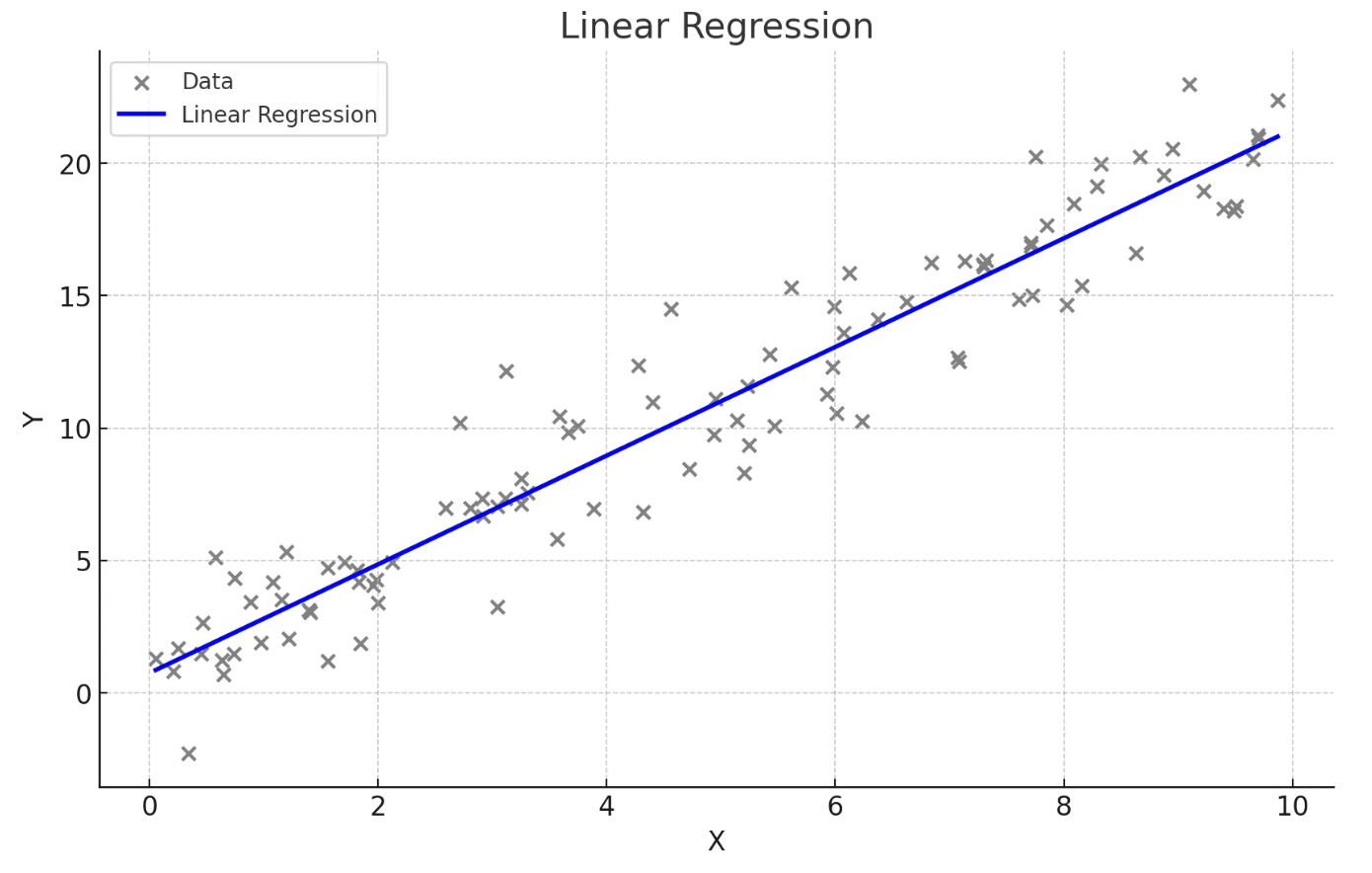
- 하나의 독립 변수(X)와 하나의 종속 변수(Y) 간의 관계를 직선으로 모델링하는 방법
- 회귀식 : Y = β0 + β1X, 여기서 β0는 절편, β1는 기울기
- 독립 변수의 변화에 따라 종속 변수가 어떻게 변화하는지 설명하고 예측
- 데이터가 직선적 경향을 따를 때 사용
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
# 예시 데이터 생성
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 단순선형회귀 모델 생성 및 훈련
model = LinearRegression()
model.fit(X_train, y_train)
# 예측
y_pred = model.predict(X_test)
# 회귀 계수 및 절편 출력
print("회귀 계수:", model.coef_)
print("절편:", model.intercept_)
# 모델 평가
mse = mean_squared_error(y_test, y_pred) # 낮을수록 좋음
r2 = r2_score(y_test, y_pred) # 높을수록 좋음
print("평균 제곱 오차(MSE):", mse)
print("결정 계수(R2):", r2)
# 시각화
plt.scatter(X, y, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=2)
plt.title('linear regeression')
plt.xlabel('X : cost')
plt.ylabel('Y : sales')
plt.show()
다중선형회귀
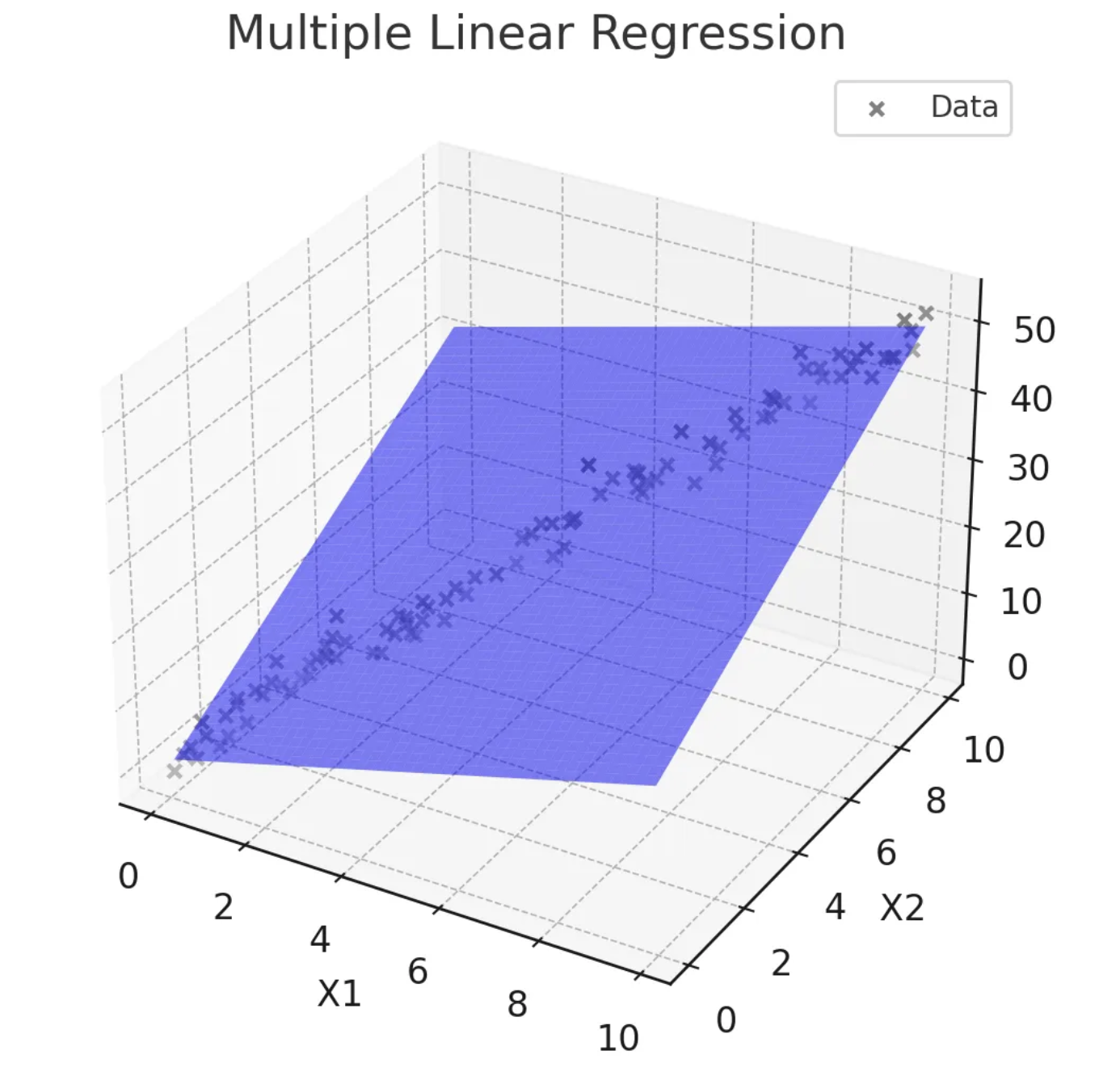
- 두 개 이상의 독립 변수(X1, X2, ..., Xn)와 하나의 종속 변수(Y) 간의 관계를 모델링
- 회귀식 : Y = β0 + β1X1 + β2X2 + ... + βnXn
- 여러 독립 변수의 변화를 고려하여 종속 변수를 설명하고 예측
- 종속변수에 영향을 미치는 여러 독립변수가 있을 때 사용
- 변수들 간의 다중공선성 문제가 발생할 수 있음
-다중공선성 : 독립 변수들 간에 높은 상관관계가 있는 경우로 각 변수의 개별적인 효과를 분리해내기 어려워져 회귀의 해석을 어렵게 만듦
-발견방법 : 간단한 방법은 상관계수를 계산하여 높은 변수들이 있는지 확인, 정확한 방법은 분산 팽창 계수(VIF)를 계산하여 10보다 높은지 확인
-해결방법 : 높은 계수를 가진 변수 중 하나 제거, 주성분 분석(PCA)과 같은 변수들을 효과적으로 줄이는 차원 분석 방법 적용
# 예시 데이터 생성
data = {'TV': np.random.rand(100) * 100,
'Radio': np.random.rand(100) * 50,
'Newspaper': np.random.rand(100) * 30,
'Sales': np.random.rand(100) * 100}
df = pd.DataFrame(data)
# 독립 변수(X)와 종속 변수(Y) 설정
X = df[['TV', 'Radio', 'Newspaper']] # 실제로는 상관계수 계산 먼저
y = df['Sales']
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 다중선형회귀 모델 생성 및 훈련
model = LinearRegression()
model.fit(X_train, y_train)
# 예측
y_pred = model.predict(X_test)
# 회귀 계수 및 절편 출력
print("회귀 계수:", model.coef_)
print("절편:", model.intercept_)
# 모델 평가
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print("평균 제곱 오차(MSE):", mse)
print("결정 계수(R2):", r2)
범주형 변수
- 범주형 변수의 경우 특별히 변환을 해주어야 함
- 순서가 있는 경우 : 각 문자를 임의의 숫자로 변환(순서가 잘 반영될 수 있게 숫자로 변환)
- 순서가 없는 경우 : 2개 밖에 없는 경우 임의의 숫자로 바로 변환해도 문제가 없지만 3개 이상인 경우에는 무조건 원-핫 인코딩(하나만 1이고 나머지는 0인 벡터)변환을 해주어야 함 → pandas의 get_dummies를 활용하여 쉽게 구현 가능
# 예시 데이터 생성
data = {'Gender': ['Male', 'Female', 'Female', 'Male', 'Male'],
'Experience': [5, 7, 10, 3, 8],
'Salary': [50, 60, 65, 40, 55]}
df = pd.DataFrame(data)
# 범주형 변수 더미 변수로 변환
df = pd.get_dummies(df, drop_first=True)
# 독립 변수(X)와 종속 변수(Y) 설정
X = df[['Experience', 'Gender_Male']]
y = df['Salary']
# 단순선형회귀 모델 생성 및 훈련
model = LinearRegression()
model.fit(X, y)
# 예측
y_pred = model.predict(X)
# 회귀 계수 및 절편 출력
print("회귀 계수:", model.coef_)
print("절편:", model.intercept_)
# 모델 평가
mse = mean_squared_error(y, y_pred)
r2 = r2_score(y, y_pred)
print("평균 제곱 오차(MSE):", mse)
print("결정 계수(R2):", r2)
비선형회귀
다항회귀
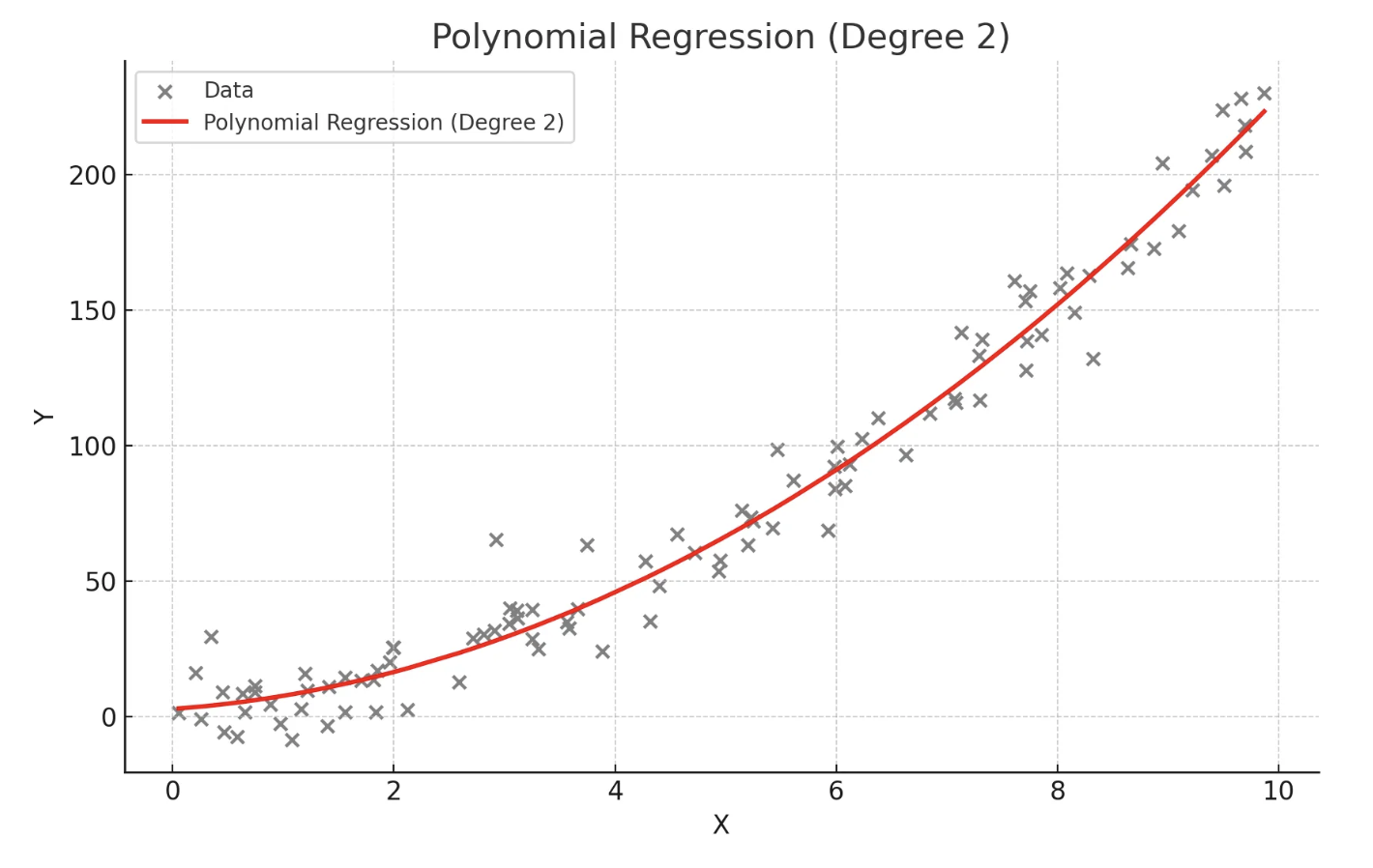
- 독립 변수와 종속 변수 간의 관계가 선형이 아닐 때 사용
- 독립 변수의 다항식을 사용하여 종속 변수를 예측
- 데이터가 곡선적 경향을 따를 때 사용
- 고차 다항식의 경우 과적합(overfitting) 위험이 있음
from sklearn.preprocessing import PolynomialFeatures
# 예시 데이터 생성
np.random.seed(0)
X = 2 - 3 * np.random.normal(0, 1, 100)
y = X - 2 * (X ** 2) + np.random.normal(-3, 3, 100)
X = X[:, np.newaxis]
# 다항 회귀 (2차)
polynomial_features = PolynomialFeatures(degree=2)
X_poly = polynomial_features.fit_transform(X)
model = LinearRegression()
model.fit(X_poly, y)
y_poly_pred = model.predict(X_poly)
# 모델 평가
mse = mean_squared_error(y, y_poly_pred)
r2 = r2_score(y, y_poly_pred)
print("평균 제곱 오차(MSE):", mse)
print("결정 계수(R2):", r2)
# 시각화
plt.scatter(X, y, s=10)
# 정렬된 X 값에 따른 y 값 예측
sorted_zip = sorted(zip(X, y_poly_pred))
X, y_poly_pred = zip(*sorted_zip)
plt.plot(X, y_poly_pred, color='m')
plt.title('polynomial regerssion')
plt.xlabel('area')
plt.ylabel('price')
plt.show()
스플라인회귀
- 독립 변수의 구간별로 다른 회귀식을 적용하여 복잡한 관계를 모델링
- 구간마다 다른 다항식을 사용하여 전체적으로 매끄러운 곡선 생성
- 데이터가 국부적으로 다른 패턴을 보일 때 사용
- 적절한 매듭점(knots)의 선택이 중요
2. 상관관계
피어슨 상관계수
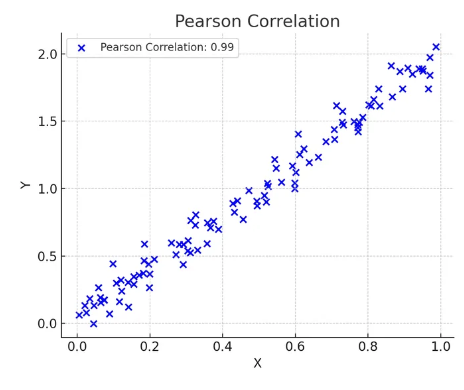
- X와 Y의 선형 관계로 두연속형 변수 간의 선형 관계를 측정하는 지표
- 데이터가 정규분포일 것이라고 가정할 수 있는 경우에만 사용
- 비선형 관계에서는 사용 불가
- -1에서 1 사이의 값을 가지며 1은 완전한 양의 선형관계, 0은 선형 관계가 없음을 의미
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import pearsonr
# 예시 데이터 생성
np.random.seed(0)
study_hours = np.random.rand(100) * 10
exam_scores = 3 * study_hours + np.random.randn(100) * 5
# 데이터프레임 생성
df = pd.DataFrame({'Study Hours': study_hours, 'Exam Scores': exam_scores})
# 피어슨 상관계수 계산
pearson_corr, _ = pearsonr(df['Study Hours'], df['Exam Scores'])
print(f"피어슨 상관계수: {pearson_corr}")
# 상관관계 히트맵 시각화
sns.heatmap(df.corr(), annot=True, cmap='coolwarm', vmin=-1, vmax=1)
plt.title('pearson coefficient heatmap')
plt.show()
비모수 상관계수
- 데이터가 정규분포를 따르지 않거나 변수들이 순서형 데이터일 때 사용하는 상관계수
- 데이터의 분포에 대한 가정 없이 두 변수 간의 상관관계를 측정할 때 사용
스피어만 상관계수
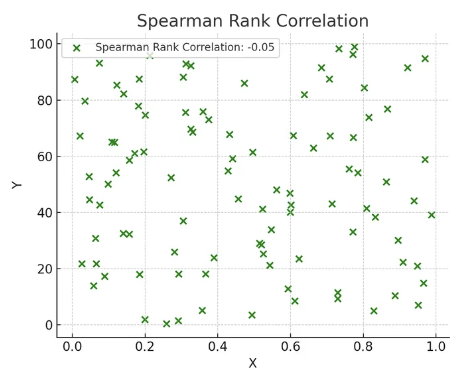
- 스피어만 상관계수는 두 변수 순위 간의 상관 관계 측정
- 값은 -1에서 1 사이로 해석
- 두 변수의 순위 간의 일관성을 측정
- 켄달의 타우 상관계수 보다 데이터 내 편차와 에러에 민감
켄달의 타우 상관계수
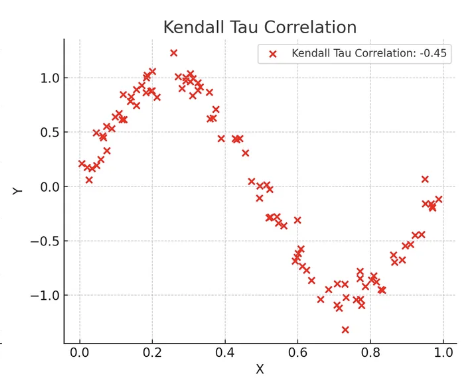
- 두 변수 간의 순위 일관성 측정
- 비선형 관계를 탐지하는 데 유용
- 순위 간의 일치 쌍 및 불일치 쌍의 비율을 바탕으로 계산
코드
from scipy.stats import spearmanr, kendalltau
# 예시 데이터 생성
np.random.seed(0)
customer_satisfaction = np.random.rand(100)
repurchase_intent = 3 * customer_satisfaction + np.random.randn(100) * 0.5
# 데이터프레임 생성
df = pd.DataFrame({'Customer Satisfaction': customer_satisfaction, 'Repurchase Intent': repurchase_intent})
# 스피어만 상관계수 계산
spearman_corr, _ = spearmanr(df['Customer Satisfaction'], df['Repurchase Intent'])
print(f"스피어만 상관계수: {spearman_corr}")
# 켄달의 타우 상관계수 계산
kendall_corr, _ = kendalltau(df['Customer Satisfaction'], df['Repurchase Intent'])
print(f"켄달의 타우 상관계수: {kendall_corr}")
# 상관관계 히트맵 시각화
sns.heatmap(df.corr(method='spearman'), annot=True, cmap='coolwarm', vmin=-1, vmax=1)
plt.title('spearman coefficient heatmap')
plt.show()
상호정보 상관계수
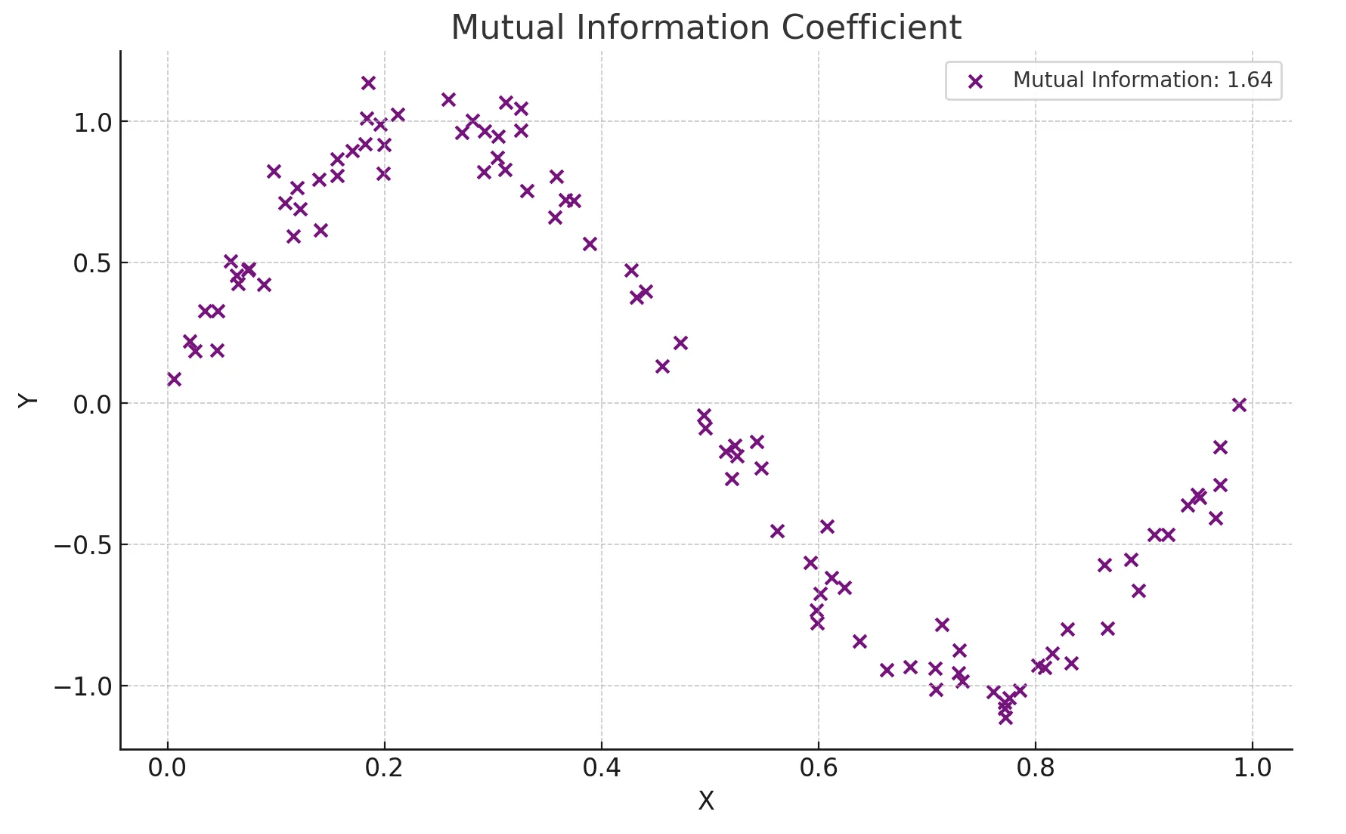
- 변수 간의 정보 의존성을 바탕으로 비선형 관계를 탐지
- 비선형적이고 복잡한 관계를 탐지하고자 할 때 사용
- 서로의 정보에 대한 불확실성을 줄이는 정도를 바탕으로 계산
- 범주형 데이터에 대해서도 적용 가능
import numpy as np
from sklearn.metrics import mutual_info_score
# 범주형 예제 데이터
X = np.array(['cat', 'dog', 'cat', 'cat', 'dog', 'dog', 'cat', 'dog', 'dog', 'cat'])
Y = np.array(['high', 'low', 'high', 'high', 'low', 'low', 'high', 'low', 'low', 'high'])
# 상호 정보량 계산
mi = mutual_info_score(X, Y)
print(f"Mutual Information (categorical): {mi}")
3. 가설검정의 주의점
재현 가능성
- 동일한 연구나 실험을 반복했을 때 일관된 결과가 나오는지 여부
- 연구의 신뢰성을 높이는 중요한 요소
- 가설검정 원리상의 문제나 가설검정의 잘못된 사용이 낮은 재현성으로 이어진다는 문제 발생
- 원인 : 실험 조건을 동일하게 조성하기 어려움, 가설검정 사용방법에 있어서 잘못됨
- 어떤 논문에서는 유의수준을 0.005로 설정하면서 데이터 수를 70% 더 늘려서 베타 값도 컨트롤 하는 방향을 제안하기도 함
- 잘못된 가설을 세우더라도 우연히 0.05보다 낮아서 가설이 맞는것처럼 보일 수도 있으므로 가능한 좋은 가설을 세우는 것도 중요
p-해킹
- 데이터 분석을 반복하여 p-값을 인위적으로 낮추는 행위
- 유의미한 결과를 얻기 위해 다양한 변수를 시도하거나, 데이터를 계속해서 분석하는 등의 방법 포함
- 여러 가설 검정을 시도하여 유의미한 p-값을 얻을 때까지 반복 분석하는 것을 조심
- 가능한 가설을 미리 세우고 검증하는 가설검증형 방식으로 분석을 해야 하며 만약 탐색적으로 분석한 경우 가능한 모든 변수를 보고하고 본페로니 보정과 같은 방법을 사용해야 함
선택적 보고
- 유의미한 결과만을 보고하고, 유의미하지 않은 결과는 보고하지 않는 행위
- 이는 데이터 분석의 결과를 왜곡하고, 신뢰성을 저하시킴
자료수집 중단 시점 결정
- 데이터 수집을 시작하기 전에 언제 수집을 중단할지 명확하게 결정하지 않으면, 원하는 결과가 나올 때까지 데이터를 계속 수집하는 것
- 이는 결과의 신뢰성을 떨어뜨림
데이터 탐색과 검증 분리
- 데이터 탐색을 통해 가설을 설정하고, 이를 검증하기 위해 별도의 독립된 데이터셋을 사용하는 것
- 이는 데이터 과적합을 방지하고 결과의 신뢰성을 높임
- 데이터셋을 탐색용(training)과 검증용(test)으로 분리하여 사용
from sklearn.model_selection import train_test_split
# 데이터 생성
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# 데이터 분할 (탐색용 80%, 검증용 20%)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 모델 학습
model = LinearRegression()
model.fit(X_train, y_train)
# 탐색용 데이터로 예측
y_train_pred = model.predict(X_train)
# 검증용 데이터로 예측
y_test_pred = model.predict(X_test)
# 탐색용 데이터 평가
train_mse = mean_squared_error(y_train, y_train_pred)
train_r2 = r2_score(y_train, y_train_pred)
print(f"탐색용 데이터 - MSE: {train_mse}, R2: {train_r2}")
# 검증용 데이터 평가
test_mse = mean_squared_error(y_test, y_test_pred)
test_r2 = r2_score(y_test, y_test_pred)
print(f"검증용 데이터 - MSE: {test_mse}, R2: {test_r2}")






