
값을 채우는 순서를 보면 규칙을 발견할 수 있다

1. DP 배열 정의
DP 배열은 당연하게 2차원 배열을 만들어야 할 거라고 생각했다.
입력이 i, j 형태로 주어지니 DP[i][j]를 만들어야 한다.
그리고 매번 구하는 건 시간상 불가능할테니, 미리 다 구해놓고 출력만 해야한다.
그래서 DP[i][j]는 i(S), j(E)의 팰린드롬 여부이다.
2. DP[i][j]는 어떻게 만들어지는가?
길이 1 팰린드롬이다.
이건 그냥 문제의 규칙이다.
길이 2 팰린드롬은 어떻게 만들어질까?
길이 2는 규칙성이라고 할 것이 딱히 없다.
이어진 두 값이 같으면 팰린드롬이다.
길이 3 팰린드롬은 어떻게 만들어질까?
길이 2에서 올 수 있을까?
A B X이런 수열이 있다고 생각해보자.
이수열은 팰린드롬이고, 여기서 길이 3 팰린드롬이 되려면 어디를 확인해야할까?
A와 X가 같기만 하면, 팰린드롬이 된다.
길이 4 팰린드롬은 어떻게 만들어질까?
A B C X이런 수열에서는 길이 2인 B와 C가 팰린드롬이고, A와 X가 같으면 팰린드롬이다.
그렇다면 DP 배열에 이미 팰린드롬의 여부를 저장하기로 했으니,
더 짧은 길이에서 더 긴 길이로 연장을 하면서 따져보면 될 거 같다.
그런데 길이 2인 B와 C팰린드롬은 DP배열상 더 높은 i행에 위치해있다.
즉, DP 배열을 상상해보자.
1은 팰린드롬, 0은 팰린드롬 X, X는 사용하지 않는 칸이다.
arr
= A B C X
= 1 2 2 1
i·j 1 2 3 4
1 1 0 0 ←
2 X 1 1 0
3 X X 1 0
4 X X X 1즉, 이 때 dp[1][4]을 채우려면, dp[2][3]이 1이어야 한다는 의미다.
dp[2][3]은 arr[2] 와 arr[3]이 팰린드롬인지를 나타내는 값이다.
팰린드롬이라면, B와 C가 같은 값이라는 뜻이고, arr[1]과 arr[4]가 같다면 길이 4인 팰린드롬이 가능하다는 뜻이다.
아까 길이 3인 팰린드롬이 만들어질 때는 딱히 규칙을 발견하지 못 했고,
길이 4인 팰린드롬을 만들어보면서 규칙을 발견했다.
그러나 길이 5인 팰린드롬을 생각해보면 확실하게 알 수 있다.
이렇게 2, 3, 4 번째 숫자가 팰린드롬이라는 것이 확인되었다면,
1, 5 번째 숫자가 같다면 길이 5인 팰린드롬을 만들 수 있다.
1 2 3 2 1
↑ ↑이렇게 말이다.
이때, 2, 3, 4 번째 숫자가 팰린드롬이라는 것이 확인이 값은 어디에 저장돼 있을까?
마찬가지다 이건 DP[2][4]에 저장돼 있다.
이제 완벽하게 규칙이 보이는가?!
그렇다면, 점화식은 이렇게 만들 수 있다.
if arr[i] = arr[j] and dp[i+1][j-1] == 1, then dp[i][j] = 1
3. 초기값 설정
점화식은 봤듯이, 길이 3 팰린드롬에서부터 동작한다.
그렇다면 길이 2와 1 팰린드롬을 초기값으로 설정해주면 되는 것이다!
위에서 언급했듯이, 길이 1은 무조건 팰린드롬이고, 길이 2는 이어진 두 값이 같으면 팰린드롬이다.
그럼 이 두 개를 초기값으로 저장해주고, 범위 지정만 잘 해준다면 모든 DP 배열을 채울 수 있을 것이다!
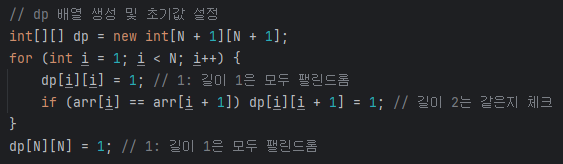
점화식을 돌릴 때, 범위 설정이 꽤나 까다로웠다.
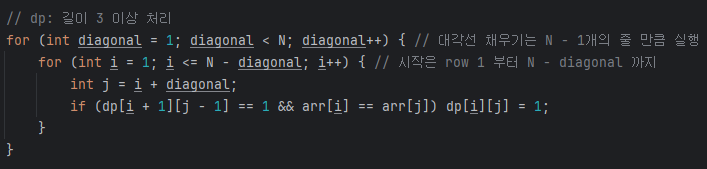
방식은 자기가 하고 싶은대로하면 되는데, 나는 대각선을 한 줄씩 채운다고 생각하면서 diagonal 변수를 생각하면서 작성했다.

정답
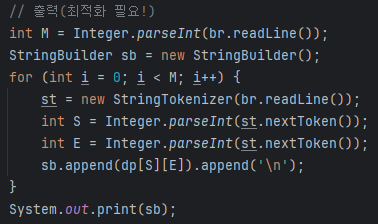
한 번 시간 초과가나서 코드를 수정했는데, 출력을 최적화 해야한다.
출력이 여러 번 발생하면 System.out.println(); 을 단순히 여러 번 할 때, 매우 많은 시간이 걸린다.
그럴 때는 BufferedWriter를 사용해서 출력 시간을 빠르게 조정하거나,
StringBuilder를 사용해서 출력을 모두 모은 다음에 딱 한 번만 출력을 하면 된다!
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// N 입력 받기
int N = Integer.parseInt(br.readLine());
// 수열 입력 받기
StringTokenizer st = new StringTokenizer(br.readLine());
int[] arr = new int[N + 1];
for (int i = 1; i <= N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
// dp 배열 생성 및 초기값 설정
int[][] dp = new int[N + 1][N + 1];
for (int i = 1; i < N; i++) {
dp[i][i] = 1; // 1: 길이 1은 모두 팰린드롬
if (arr[i] == arr[i + 1]) dp[i][i + 1] = 1; // 길이 2는 같은지 체크
}
dp[N][N] = 1; // 1: 길이 1은 모두 팰린드롬
// dp: 길이 3 이상 처리
for (int diagonal = 1; diagonal < N; diagonal++) { // 대각선 채우기는 N - 1개의 줄 만큼 실행
for (int i = 1; i <= N - diagonal; i++) { // 시작은 row 1 부터 N - diagonal까지
int j = i + diagonal;
if (dp[i + 1][j - 1] == 1 && arr[i] == arr[j]) dp[i][j] = 1;
}
}
// 출력(최적화 필요!)
int M = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int S = Integer.parseInt(st.nextToken());
int E = Integer.parseInt(st.nextToken());
sb.append(dp[S][E]).append('\n');
}
System.out.print(sb);
}
}