[Java] 1915번: 가장 큰 정사각형 Gold 4

문제 링크

꽤나 참신한 문제가 아니었나 싶다..

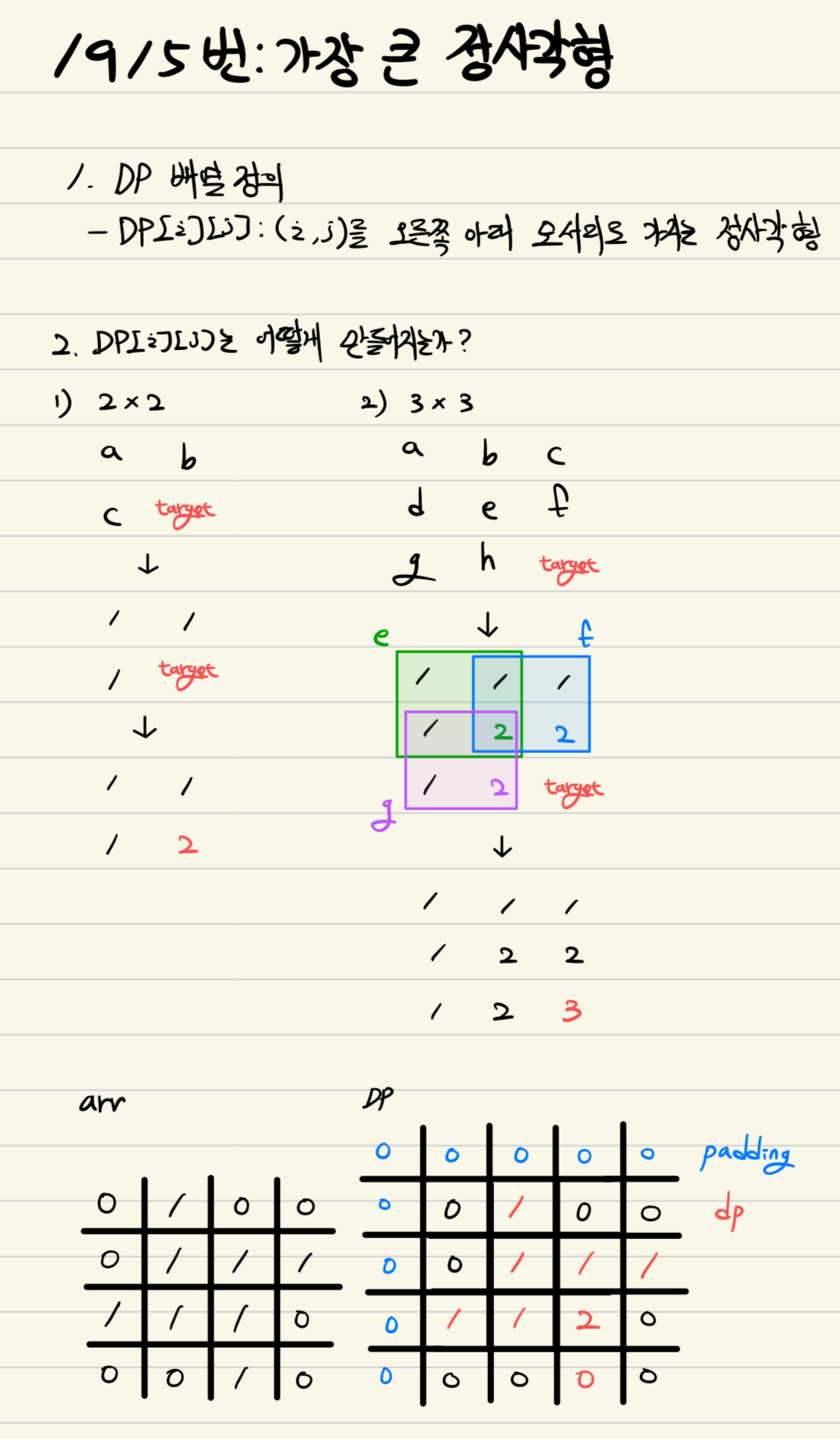
1. DP 배열 정의

DP[i][j]를 정의해야 했다.
2차원을 모두 살펴봐야하는 건 당연하다.
그래서 DP[i][j]로 했고, 두 가지를 생각할 수 있었다.

1. (i,j)까지 살펴봤을 때의 정사각형의 최대 넓이
2. (i,j)를 오른쪽 아래 모서리로 가지는 정사각형의 넓이

결론부터 말하자면, 1번의 정의는 의미가 없었다.

왜냐하면 중간에 1이 한 개라도 끊킨다면, 결국에 사각형을 만들 수가 없기 때문이다.

즉 (i,j)좌표를 기준으로 왼쪽, 왼쪽 위, 위 이 세 곳이 모두 1로 채워져 있어야만 정사각형을 만들 수 있다.

그래서 2번의 정의를 사용해야 한다.

2. DP[i][j]는 어떻게 만들어지는가?

바로 방금 위에서 왼쪽, 왼쪽 위, 위 이 세 곳이 모두 1로 채워져 있어야만 이렇게 말했다.

1 * 1 크기의 정사각형은 1만 있으면 된다.

2 * 2 크기를 생각해보자

당연하게도 아래와 같은 형태가 되어야만 적어도 2 * 2 크기의 정사각형을 만들 수 있다.
물론, target도 1이어야 한다.

arr
1 1
1 1

dp
1 1
1 X ←

그렇다면 target에는 4를 저장하면 된다!

3 * 3 크기를 생각해보자.

arr
a b c
d e f
g h X

target 기준으로 세 곳인 e, f, h를 살펴보면 된다.

즉, h, e, f가 모두 4면 되는 것이다.

dp
1 1 1
1 4 4
1 4 X ←

2 * 2 기준에서 생각을 해보면, e와 f와 h의 위치에서 각각 검사를 했을 때 세 곳이 모두 1이면 되는 것이다.

a, b, d가 모두 1이라면, e에는 4가 저장돼 있을 것이다.

arr
1 1 c
1 e f
g h X

dp
1 1 ?
1 4 ?
? ? X ←

b, c, e가 모두 1이라면, f에는 4가 저장돼 있을 것이다.
d, e, g가 모두 1이라면, h에는 4가 저장돼 있을 것이다.

dp
1 1 1
1 4 4
1 4 X ←

그리고 e, f, h가 모두 4라면, a, b, c, d, e, f, g, h가 모두 1이기에
target에는 9가 저장되면 되는 것이다!

arr
1 1 1
1 1 1
1 1 1

(당연히 target도 역시 1일 때)

dp
1 1 1
1 4 4
1 4 9 ←

그런데, 굳이 벌써부터 넓이를 저장할 필요가 없다.
어차피 정사각형이기 때문에 한 변의 길이를 저장하면 된다.

dp
1 1 1
1 2 2
1 2 3 ←

세 곳중에 한 곳이라도 1이 아니라면 어떻게 될까?

arr
1 0
1 1 ←

1이 아닌 곳의 dp 배열에는 0이 저장돼 있을 것이다.

dp
1 0
1 X ←

그리고 현재의 위치는 1이었기에 그 검사를 한 것이고,
최대 넓이는 현재 위치의 1만을 고려할 수 있으므로 1*1크기의 정사각형이 된다.

이런 경우는 어떻게 될까?

arr
1 1 1
1 1 1
  ↑ ↑

최대로 만들 수 있는 크기는 2 * 2이다.
(2.2)나 (2,3)를 오른쪽 모서리로 갖는 정사각형이 최대 넓이다.

이 때 실제로 만들어져야 하는 dp 배열은 이렇다.

dp
1 1 1
1 2 2

내가 말한 조건은 세 곳의 값이 모두 동일할 때, 변의 길이를 연장하는 것이었다.
그런데 그렇게 하면 (2,3)에 2를 저장할 수가 없다.

그렇다면 어떻게 해야될까?

세 곳의 값은 각각 1, 1, 2 다.

이 중에 모두 2였다면 3으로 연장이 가능했겠지만, 두 곳이 2보다 작은 1이다.

그말은 1인 위치에서 왼쪽, 왼쪽위, 위의 값들이 1이 아니라 0으로 1개 이상 채워져있다는 뜻이기에 길이 연장이 불가능하다는 것이다.

arr
0 1 0 ←
1 1 1
1 1 1
  ↑ ↑

그렇기에 1, 1, 2중에서 1에서부터 하나 더 연장을 한 2를 사용해야한다.

하나 더 생각해보자

세 곳의 값이 1, 2, 3이었다면 어떤 값을 사용해야할까?

실제 가능한 배열중 하나를 생각해보면 이렇게 된다.

arr
1 1 1 0
1 1 1 0
1 1 1 1
0 1 1 1 ←

dp
1 1 1 0
1 2 2 0 ←
1 2 3 1 
0 1 2 X

X의 위치에서 가장 큰 정사각형은 2가 된다.

왜냐면 1의 바로 위의 0 때문에 더 이상 정사각형을 고려할 수 없기 때문이다.

즉, DP 배열의 왼쪽, 왼쪽위, 위의 값 중에서 제일 작은 값에서 길이 1만큼 연장이 가능한 것이다!

따라서 점화식은 이렇게 된다.

if arr[i][j] == 1 then, dp[i][j] = min(dp[i-1][j], dp[i-1][j-1], dp[i][j-1]) + 1

그리고 계산의 편의를 위해서 padding을 추가하면 된다!
즉, 배열을 n+1 * m+1 크기로 만들면 된다!

이제 코드를 작성해보자

정답

한 번 틀렸는데, ans 를 1로 초기화해서 틀렸다.

1이 아예 없는 입력도 있다보다..

ans를 0으로 초기화하니 바로 통과했다!

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        // n, m 입력 받기
        StringTokenizer st = new StringTokenizer(br.readLine());
        int n = Integer.parseInt(st.nextToken());
        int m = Integer.parseInt(st.nextToken());

        // 배열 생성
        int[][] arr = new int[n][m];
        int[][] dp = new int[n + 1][m + 1];

        // 배열 입력 받기
        for (int i = 0; i < n; i++) {
            String str = br.readLine();
            for (int j = 0; j < m; j++) {
                arr[i][j] = str.charAt(j) - '0';
            }
        }

        // dp
        int ans = 0;
        for (int i = 1; i < n + 1; i++) {
            for (int j = 1; j < m + 1; j++) {
                if (arr[i-1][j-1] > 0) {
                    dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
                    ans = Math.max(ans, dp[i][j]);
                }
            }
        }

        // 출력
        System.out.println(ans * ans);
    }
}