[DL 5강] Neural Networks

SPS LAB 2025.01.23 신입생 세미나 2주차

• 본 내용은 Michigan University의 Deep Learning for Computer Vision 5강 Neural Networks 강의를 듣고 정리한 내용입니다.
• 강의의 원본은 해당 링크에서 확인하실 수 있습니다.

1. Linear Classifier

• 문제점: Linear Classifier는 매우 간단하고 이해하기 쉽지만 분류가 안 되는 경우가 다수 존재
  
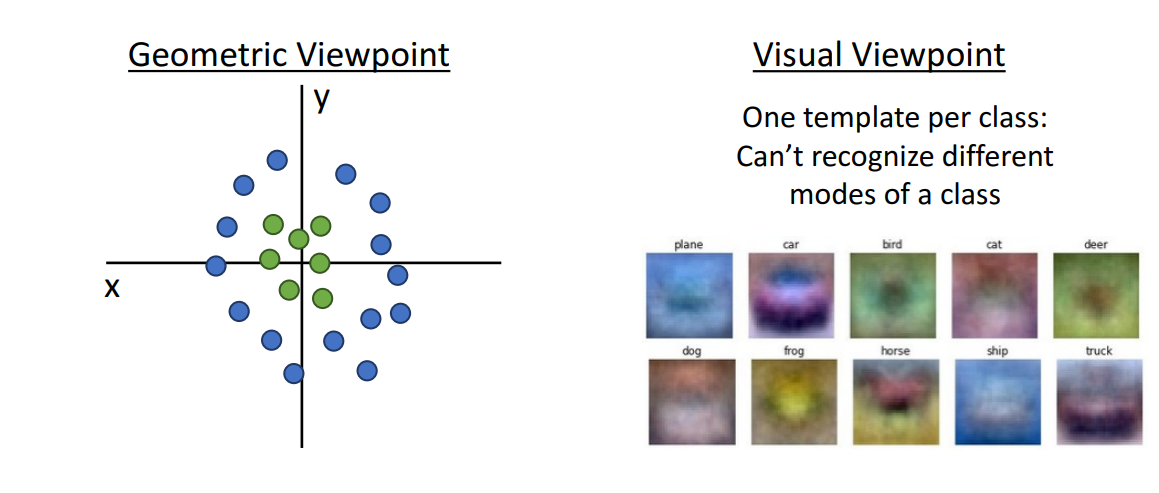
  • Geometric Viewpoint: 초록색 점과 파란색 점을 선형적으로 분류하는 것이 어려움
  • Visual Viewpoint: 하나의 template로 여러 mode 인식하는 것이 어려움
• 해결책: Feature Transforms
  • 선형 분류가 용이하게 될 수 있도록 입력 데이터에 적용
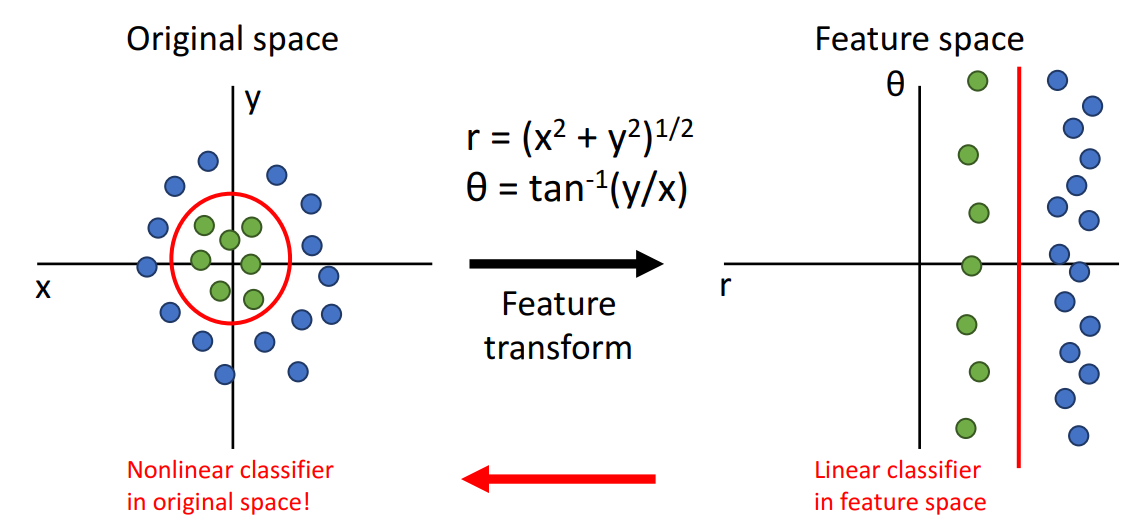
  • Feature Transform을 통해 Original space에서 Feature space로 변환하여 선형분리 가능하게 함
  • 이를 다시 original space로 변환하여 비선형적인 데이터도 분류가 가능하게 하는 것이 아이디어
    

2. Feature Representation

1. Color Histogram

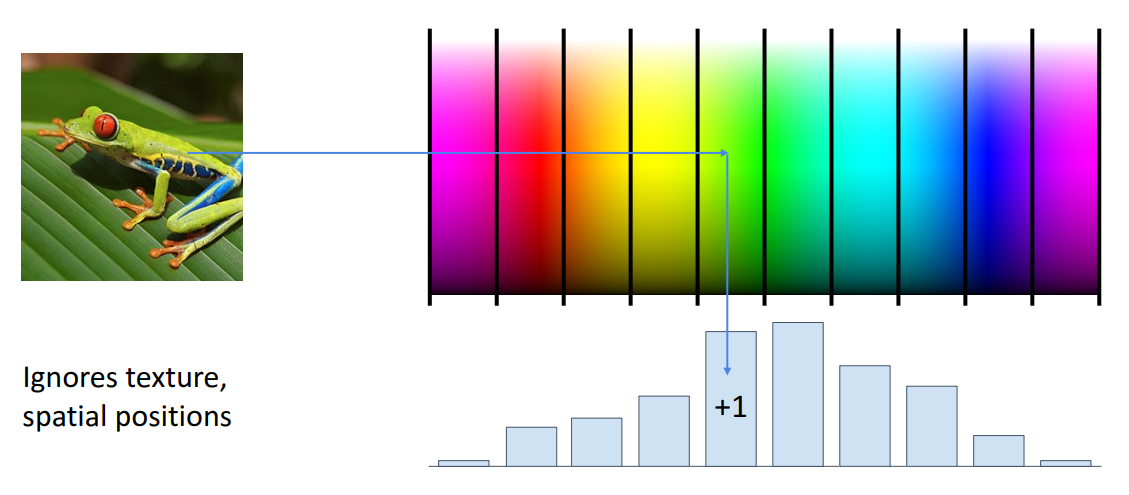
• 색상 공간을 여러 개의 개별 bin으로 나누고 색상 공간의 rgb 스펙트럼을 지정한 다음 각 픽셀과 입력 이미지에 대해 색상 공간의 bin 표현 어디에 있는지 지정할 수 있음
• 입력 이미지의 Color Histogram 표현은 어떻게든 이미지에 대한 모든 공간 정보를 버리고 어떤 유형의 색상인지만 관심을 가짐
• 예를 들어, car image에 대해 갈색 배경, 빨간 자동차와 같은 이미지에 대해 자동차가 이미지의 다른 위치에 나타날 수 있다고 가정
  • Linear Classifier는 이를 분류하는 것이 어려움
  • Color Histogram은 빨간색과 갈색으로 이를 표현

2. Histogram of Oriented Gradients (HoG)

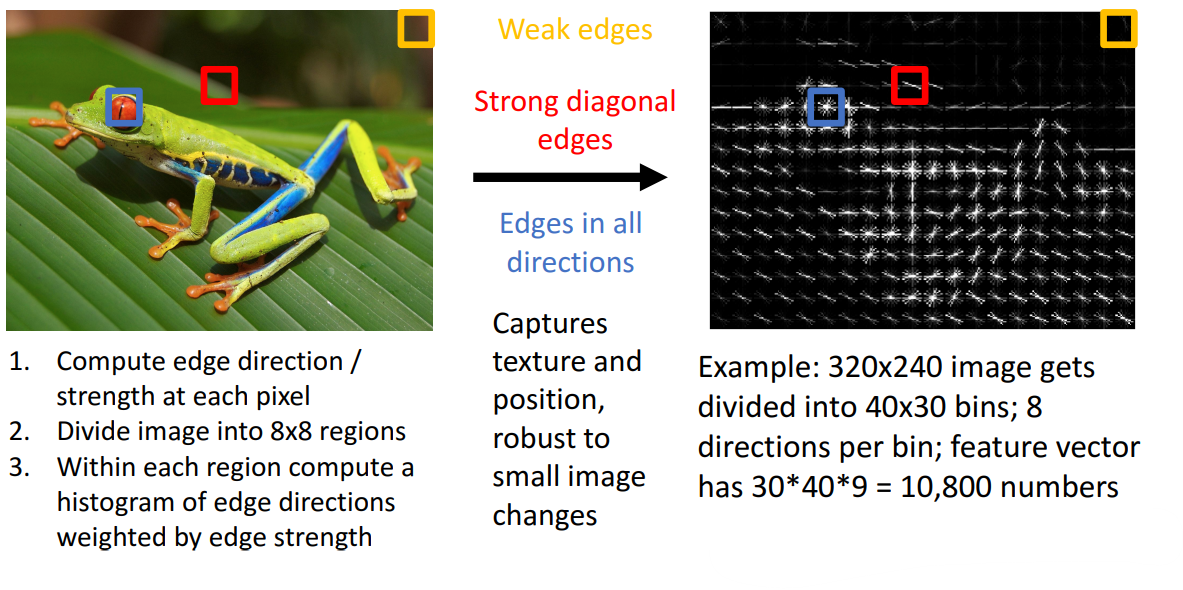
• 모든 색상 정보를 버리고, local edge 방향(orientation)과 강도(strength)만 관심을 가짐
• 입력 이미지의 모든 위치, pixel에서 edge의 로컬 방향과 강도에 대한 정보를 알려줌
• 예를 들어, 개구리 사진에서 빨간색 영역은 강한 대각선 edge가 존재, 파란색 영역은 모든 종류의 방향에 edge가 존재, 노란색 영역은 정보가 거의 업음

--> 1, 2의 방법은 2000년대 중반부터 후반까지 Object Detection 등의 다양한 Computer Vision에서 사용되었음. 하지만 사람이 input data에서 색상이 중요한지 방향이 중요한지 등을 고려해야 해서 잘 쓰이지 않는 방법론이 됨

3. Bag of Words (Data-Driven)

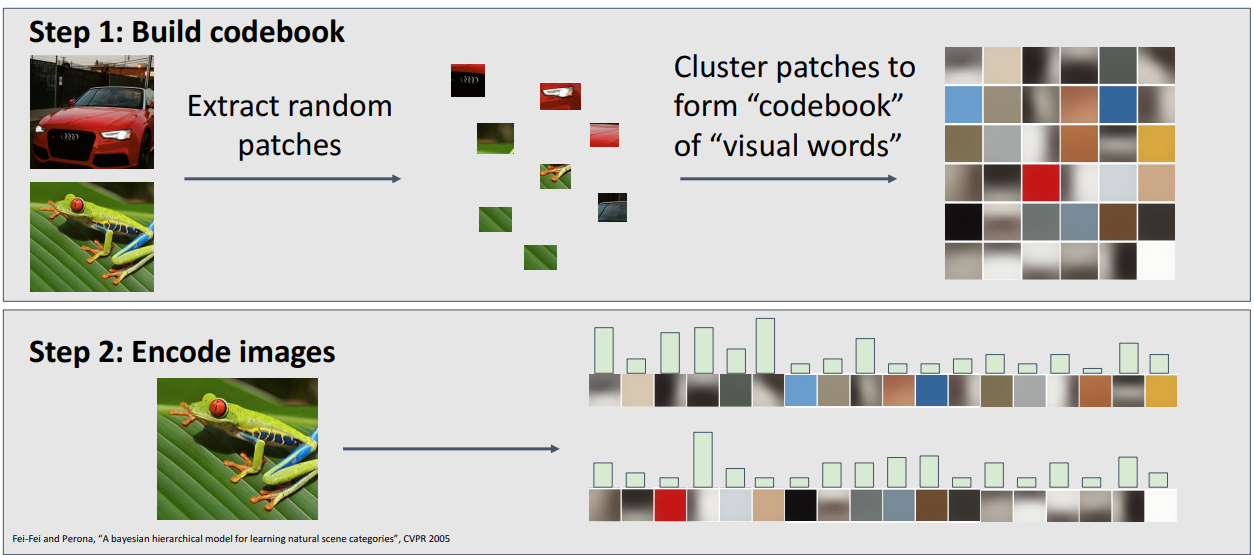
• 단계
  • Step 1. Build Codebook
    • input data에서 다양한 규모와 크기의 random patch 추출
    • random patcg를 clustering하여 visual words의 codebook을 만듬
    • 많은 이미지에서 나타는 공통적인 유형의 구조가 training 이미지에 있는 경우, 이를 포착하거나 인식할 수 있는 visual words의 codebook이 필요
  • Step 2. Encode images
    • 모든 local image patch의 클러스터 중심인 codebook을 가져와 각각에 대한 히스토그램 표현을 계산
    • 히스토그램 표현은 입력 이미지에서 visual words가 입력 이미지 표현에 얼마나 많이 나타나는지를 말함
• 장점
  • 기능적 형태를 완전히 지정할 필요가 없기 때문에 매우 강력한 유형의 기능 표현
  • 문제에 더 잘 맞도록 훈련 데이터에서 학습할 수 있으므로 유연한 방법

4. 여러 feature representation 방법의 결합

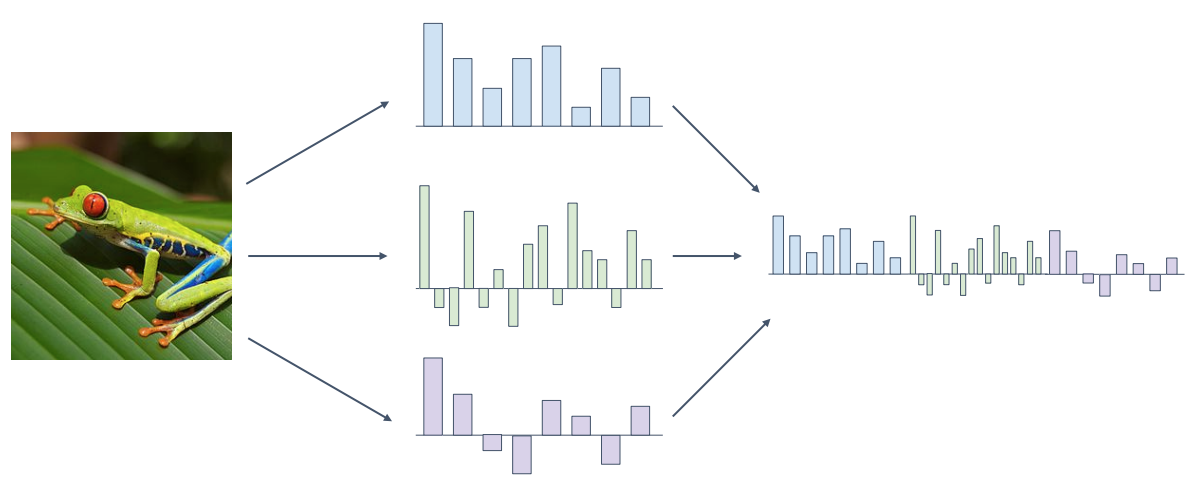
• 입력 이미지의 다양한 특징 표현을 생각하고 여러 방법을 결합하는 방식
• 실제로 2011년 ImageNet challenge에서 우승한 사람이 복잡한 기능 표현을 사용했다는 표준적인 예로 2000년대 후반과 2010년 초반에 computer vision에서 널리 사용

3. Image Features

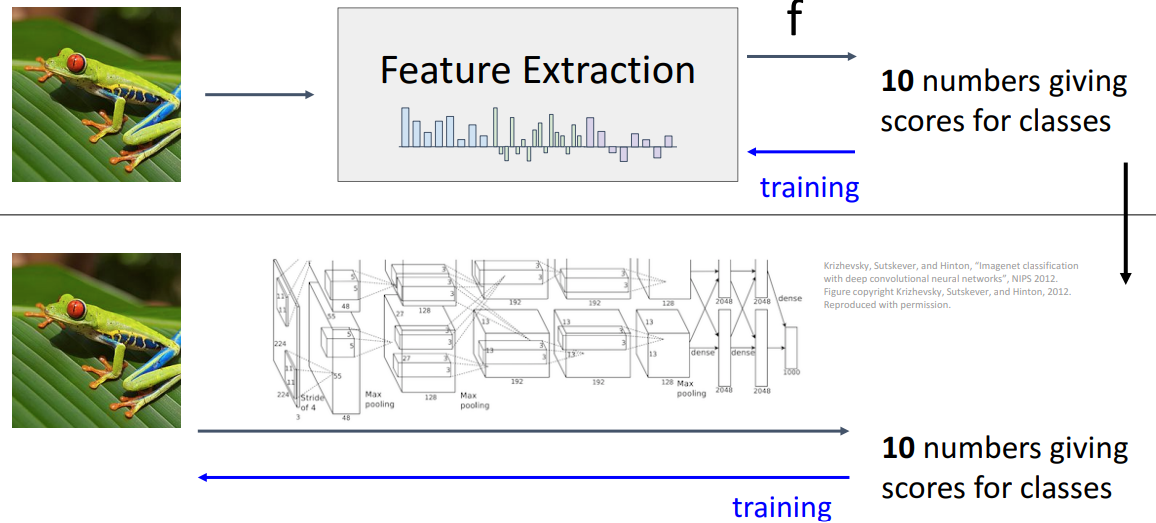
• 상단 방법
  • raw image pixel가 Feature Extraction과 추출한 feature 위에서 작동하는 learnable model을 거쳐 final classification score까지 이어지는 복잡한 시스템
  • 맨 마지막은 결국 우리 시스텥ㅁ의 분류 정확도를 최대화하려는 응답으로 가중치를 튜닝
  • 어떻게든 모든 부분을 자동으로 튜닝하는 더 나은 작업을 원한다는 Motivation에서 딥러닝 신경망 시스템을 구축할 때 신경망이 무엇을 하는지 생각하게 함
• 하단 방법
  • 신경망 기반 시스템은 기본적으로 feature representation 방식과 크게 다르지 않음
  • 신경망은 feature representation과 linear classifier를 공동으로 학습하여 시스템의 분류 성능을 극대화하는 방식

4. Neural Networks

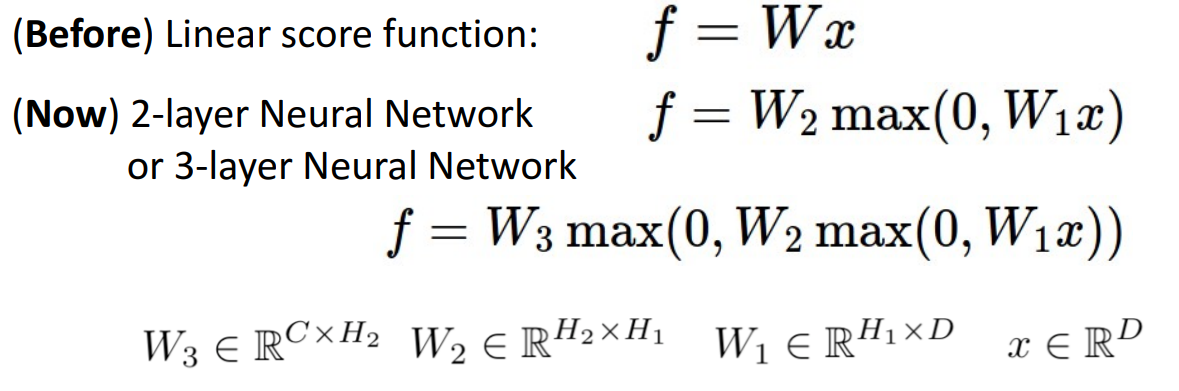
• Linear score function
  • 입력 데이터 x, 가중치 행렬 W 간에 곱으로 구성된 Linear Classifier
• 2-layer or 3-layer Neural Network
  • 신경망 모델로, 2개의 학습 가능한 가중치 행렬을 가지고 있음

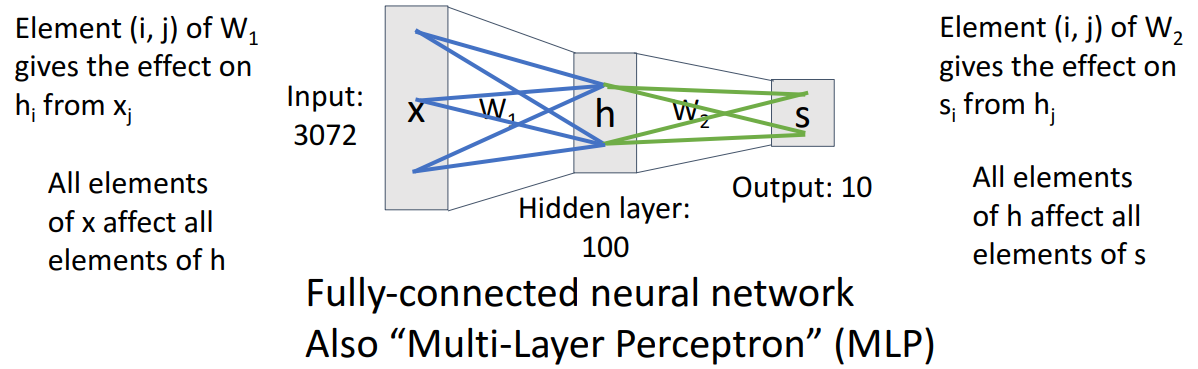
• 가중치 행렬을 이전 계층의 각 요소가 다음 계층의 요소에 얼마나 영향을 미치는지 알려주는 것으로 해석 가능
  • W1은 input vector의 각 요소가 hidden vector의 각 요소에 얼마나 영향을 미치는지 보여줌
  • W2는 hidden vector의 각 요소가 score vector의 각 요ㅛ소에 얼마나 영향을 미치는지 보여줌
• 모든 요소들이 완전히 연결되어 있는 dense connectivity pattern을 가지고 있으면 Fully-connected neural network 또는 Multi-Layer Perceptron (MLP)라고 함

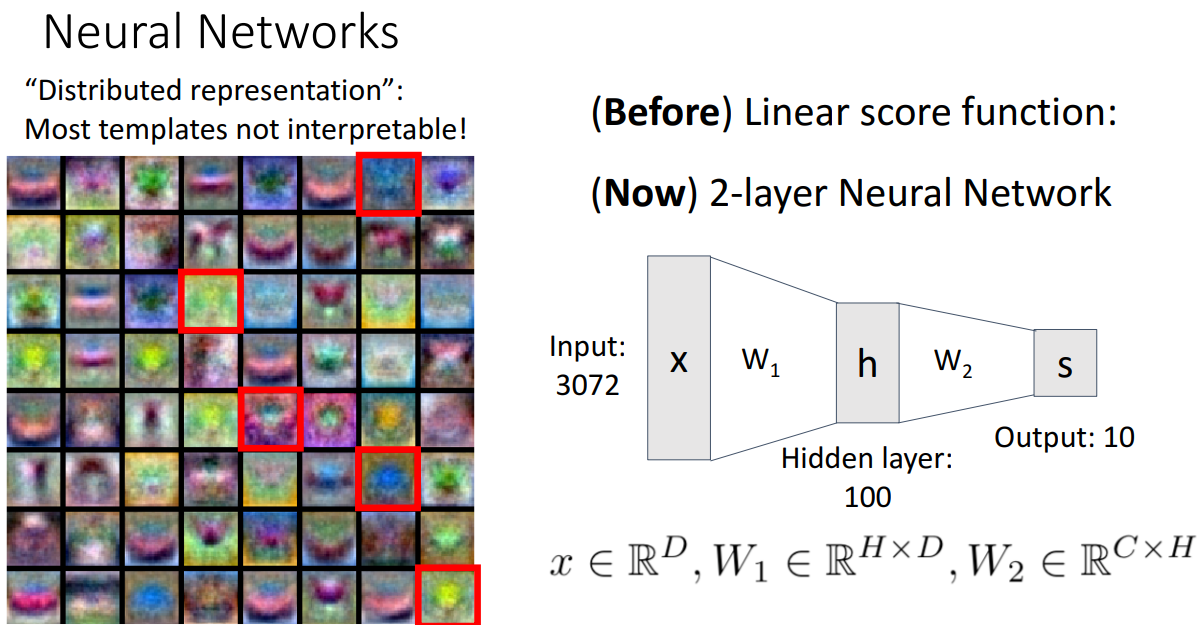
• Linear Classifier vs. Neural Network

  • Linear Classifier: Class 당 1개의 template 집합 학습, 템플릿과 입력 이미지 간의 내적을 계산하여 각 템플릿에 얼마나 일치하는지 score를 계산
  • Neural Network: 첫번째 계층은 template의 집합, 두번째 계층은 template을 가중 재조합을 톨해 분류 score를 예측

• Neural Network 특징

  • 여러 유형 또는 여러 범주의 하위 집합을 인식할 수 있음
    • 하나의 템플릿을 사용하여 왼쪽을 향하는 말과 또 다른 템플릿을 사용하여 오른쪽을 향하는 마라을 모두 인식할 수 있음
  • 이미지를 표현하기 위해 소위 분산 표현을 사용하는 네트워크

5. Deep Neural Network

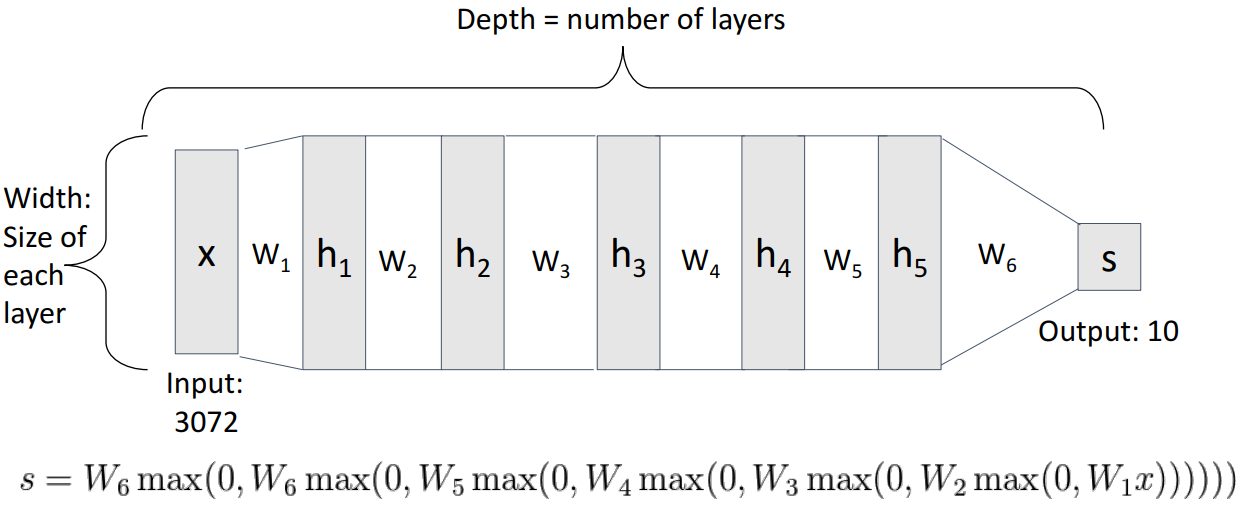
• Depth = number of layers = 가중치 행렬의 수 ex) 학습 가능한 가중치 행렬이 6개이므로 Depth 6의 레이어 네트워크
• Width = size of each layer = number of unit = 각 숨겨진 표현의 차원

6. Activation Function

• 개념
  • 신경망의 매우 중요한 특징, 구성 요소
  • 두 개의 학습 가능한 가중치 행렬 사이에 존재
  • ex) ReLU: 양수이면 그대로, 0이거나 음수이면 0을 반환하는 함수
• 질문
  • Q1. 활성화 함수가 없다면?
    • A. NN이 선형 분류기의 역할을 한다. ex) deep linearnetwork
• 종류
  

7. Space Warping

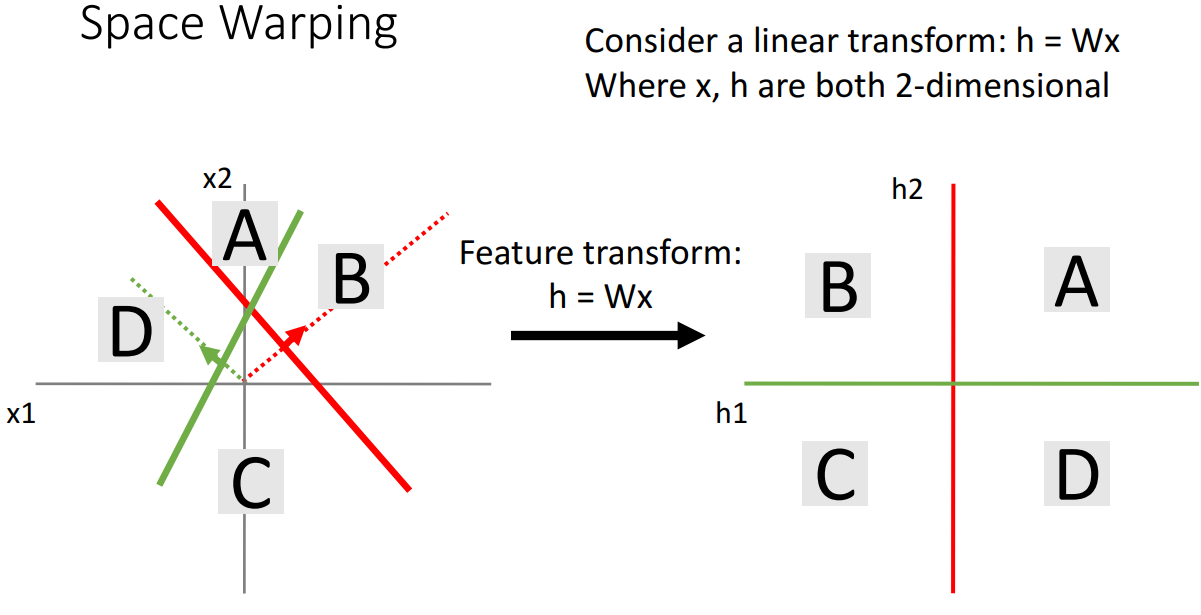
• 개념

  • 2개의 선형 클래스와 2차원 liner transform을 사용하면 입력 공간의 두 선을 통해 4개 영역을 나누고 각 영역인 4개의 사분면을 얻음

• 적용
  

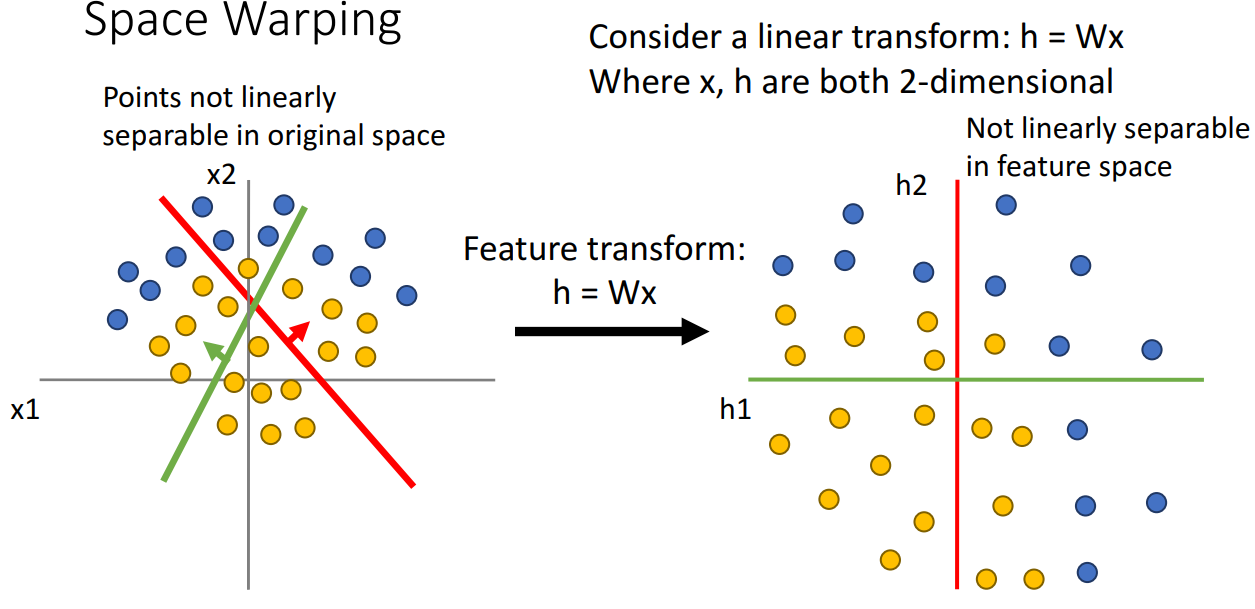
  • 선형 특징 변환 적용해보기
    - 공간을 선형적으로 휘게 하는 선형 변환을 적용하면 입력 데이터를 새로운 것으로 변환
    - 하지만 여전히 점이 선형적으로 분리될 수 없음
    
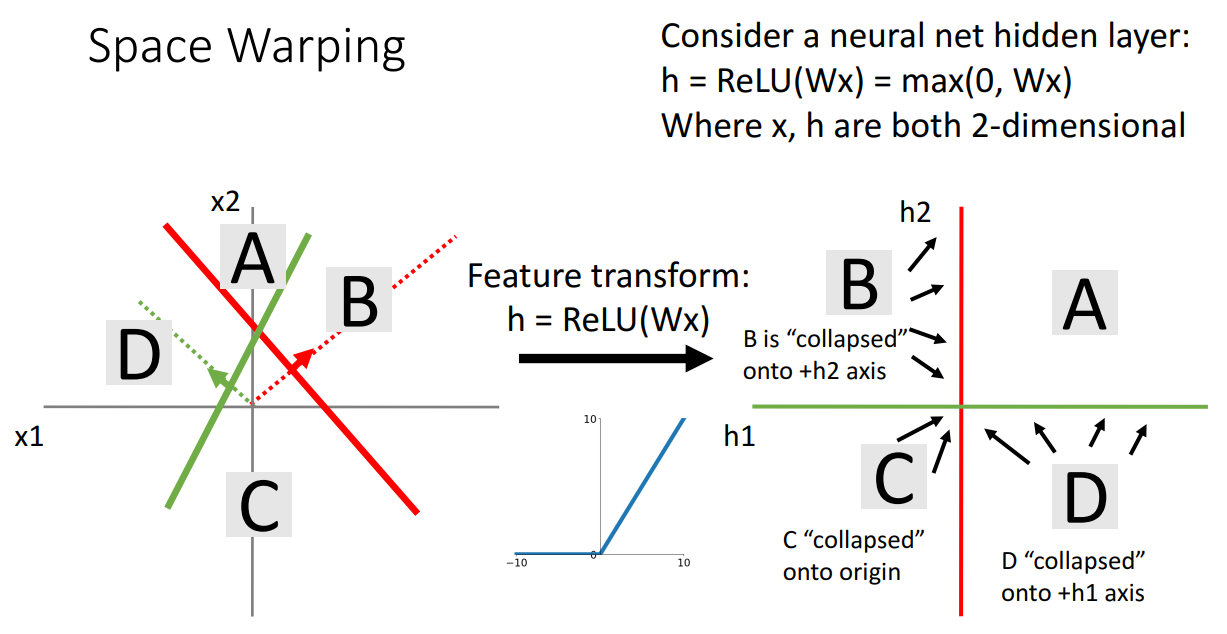
  • ReLU 함수 적용해보기
    • 변환되는 방식이 비선형 Activation function인 ReLU 적용
      • B: 빨간색 피쳐에 대해 양수 값에 해당, 녹색 피쳐에 대해 음수 값 --> 녹색 특징이 0으로 설정되어 h2 축 위에 위치
      • C: 빨간색 피쳐에 대해 음수 값에 해당, 녹색 피쳐에 대해 음수 값 --> 두 특징이 모두 0으로 설정되어 원점 위에 위치
      • D: 빨간색 피쳐에 대해 음수 값에 해당, 녹색 피쳐에 대해 양수 값 --> 빨간색 특징이 0으로 설정되어 h1 축 위에 위치
    • 실제 적용
      
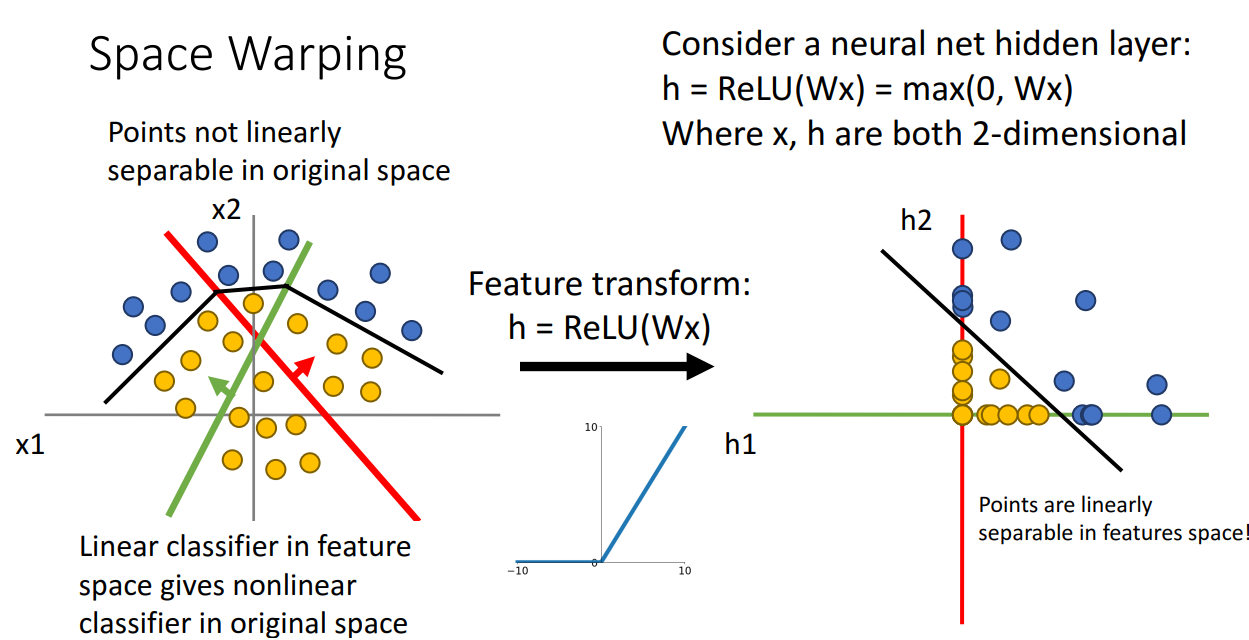
      • 선형으로 구분 가능해짐

• 주의점
  

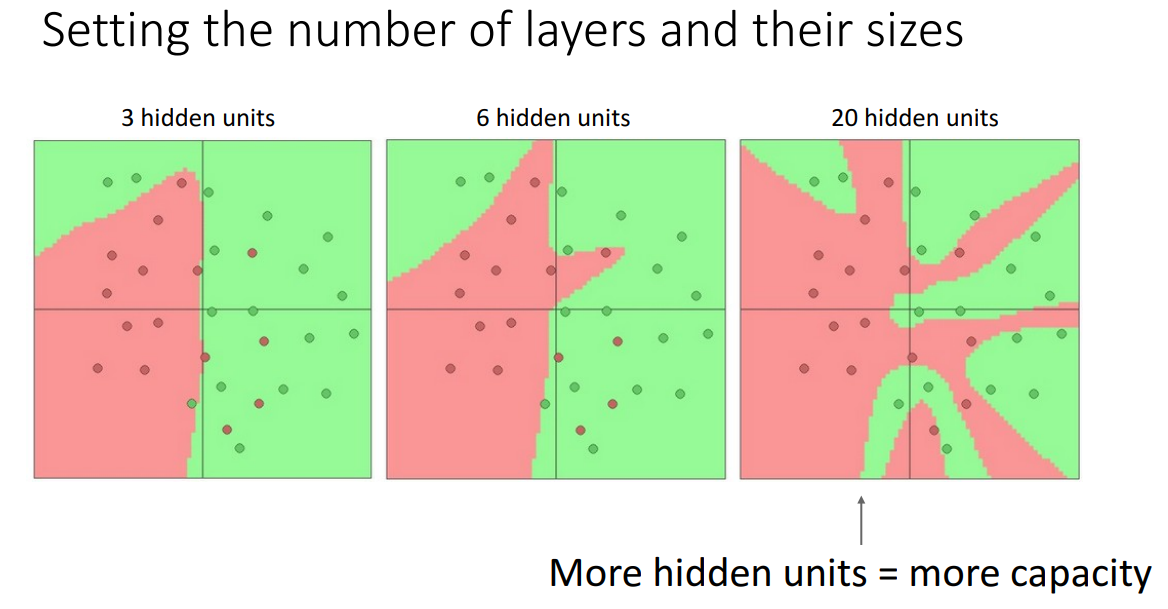
  • hidden units이 많을수록 complexity, capacity가 증가하지만, overfitting 가능성이 높아짐
    • 적절한 정규화 방식을 적용하여 일반화 성능도 보장하는 것이 중요!

8. Universal Approximation

• 개념
  • 하나의 숨겨진 레이어가 있는 신경망 시스템이 $R^N$ -> $R^M$의 모든 함수를 근사할 수 있다
  • 제한된 입력 공간에서 모든 연속 함수를 근사화할 수 있다
• 예시
  
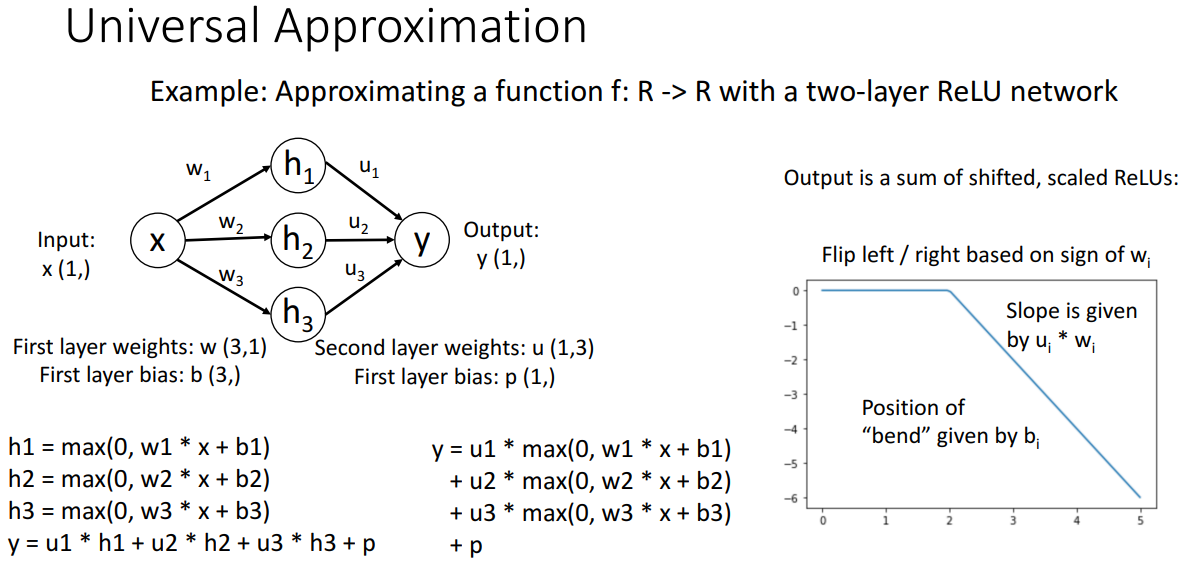
  • 입력을 단일 실수를 받고, 출력으로 단일 실수를 생서하는 rulu 기반 완전 연결 2계층 신경망
  • 출력값 y는 계층 값의 선형 조합
• bump
  
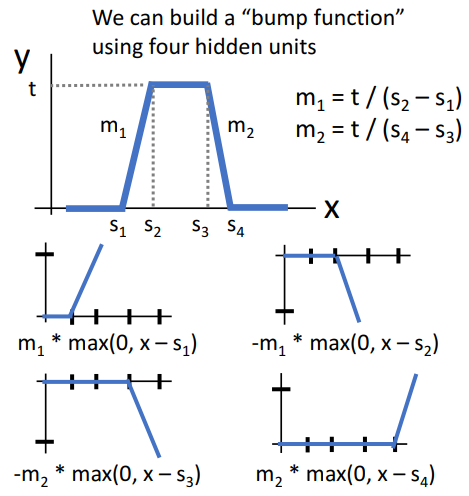
  • 범프의 출력이 4개의 relu 함수의 선형 조합인 것을 확인할 수 있음
    
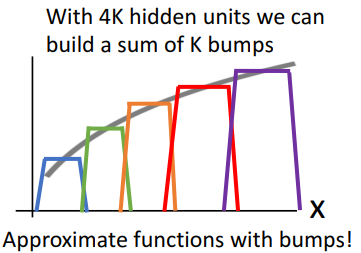
  • 범프들을 합쳐 원하는 모든 유형의 연속 함수에 완벽하게 근접하도록 배치할 수 있음
  • 범프들을 추가하거나, 범프들 간의 gap을 작게 하여 더 근접하게 만들 수 있음

9. Convex Functions

• 개념
  

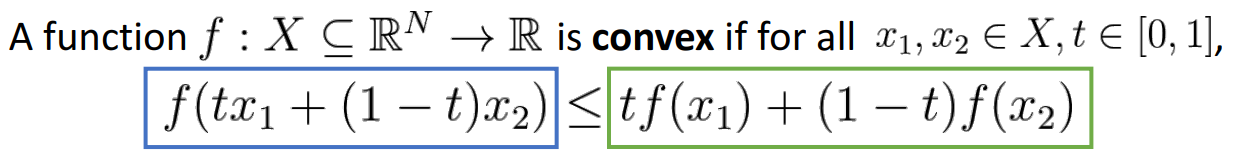
  • 해당 조건 성립하면 convex하다고 함
  • convex function은 쉽게 최적화를 할 수 있고, global minimum에 수렴하는 것을 이론적으로 보장할 수 있음

• 예시
  

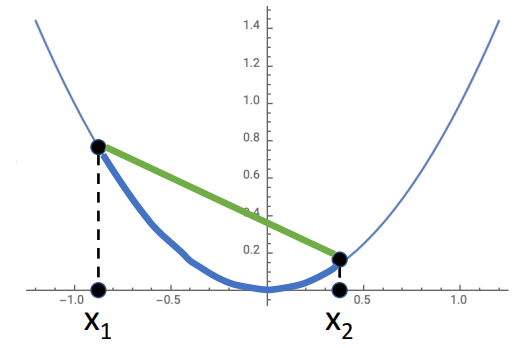
  ex1) $f(x) = x^2$ - convex
  

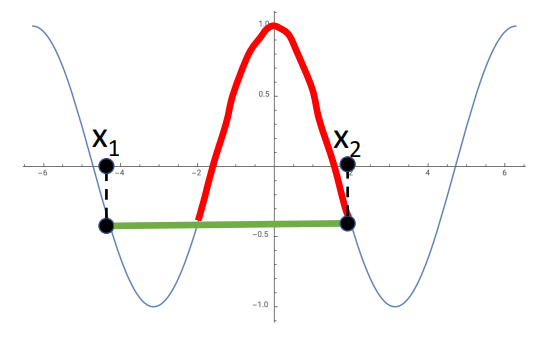
  ex2) $f(x) = cos(x)$ - not convex

  

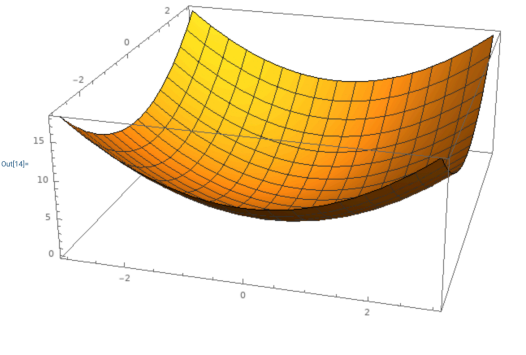
  ex3) 고차원에서의 볼록성: bow한 모양 (그릇 모양의 함수)