SPS LAB 2025.01.23 신입생 세미나 2주차
- 본 내용은 Michigan University의 Deep Learning for Computer Vision 6강 Backpropagation 강의를 듣고 정리한 내용입니다.
- 강의의 원본은 해당 링크에서 확인하실 수 있습니다.
1. gradient를 어떻게 계산할 것인가?

idea 1. Derive on paper

- 개념
- 종이에 기울기를 유도하는 것 (Bad idea!)
- 단점
- 매우 지루함
- 많은 양의 종이가 필요함
- 모듈적 설계로 이어지지 않음
- 복잡한 모델에서는 실행 가능성이 높지 않고 확장성이 지극히 낮음
idea 2. Computational Graphs
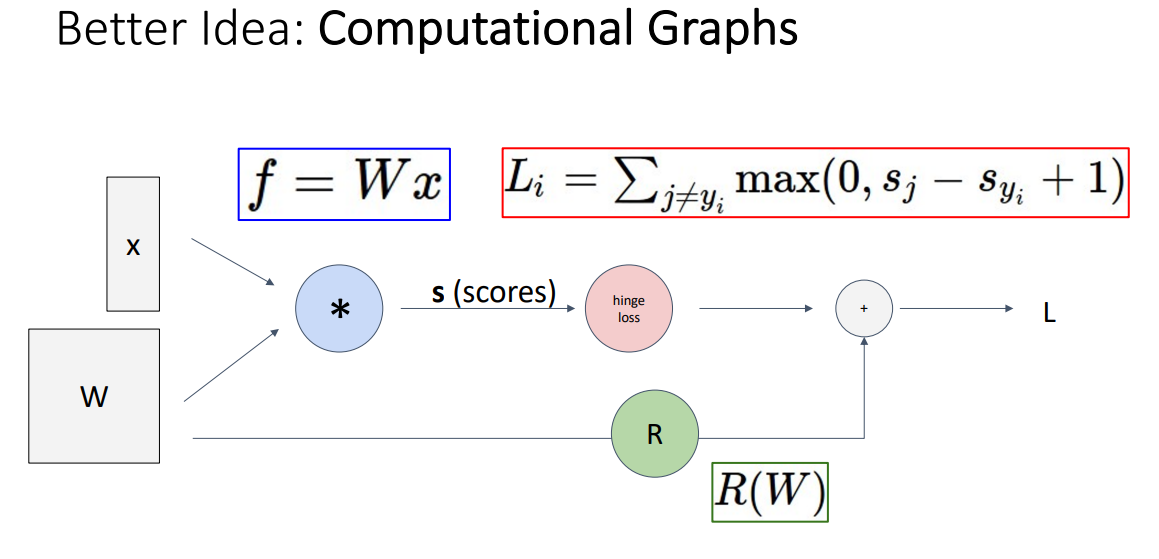
- 개념
- 그래디언트 계산 문제를 해결하는 데 도움이 되는 구조로, 모델 내부에서 수행한 계산을 나타내는 방향 그래프 (Better idea!)
- Neural Turing Machine
- 계산 그래프 구조 위에서 자동으로 그래디언트를 계산하는 것이 가능
- 복잡한 신경망 모델에서 그래디언트를 계산하기 위해 계산 그래프를 사용하는 것이 정말로 중요한 이유!
2. Backpropagation
계산 그래프에서 gradient를 계산하기 위해 사용하는 알고리즘
1. Simple Example
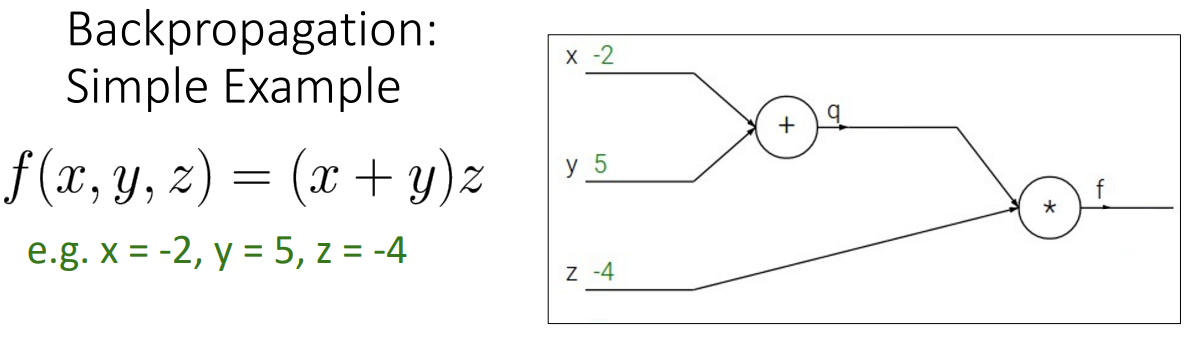
- Step 1. Forward pass
- 왼쪽에서 오른쪽으로 진행하는 모든 작업을 수행하여 출력을 계산
ex) 이고, 이므로
- 왼쪽에서 오른쪽으로 진행하는 모든 작업을 수행하여 출력을 계산
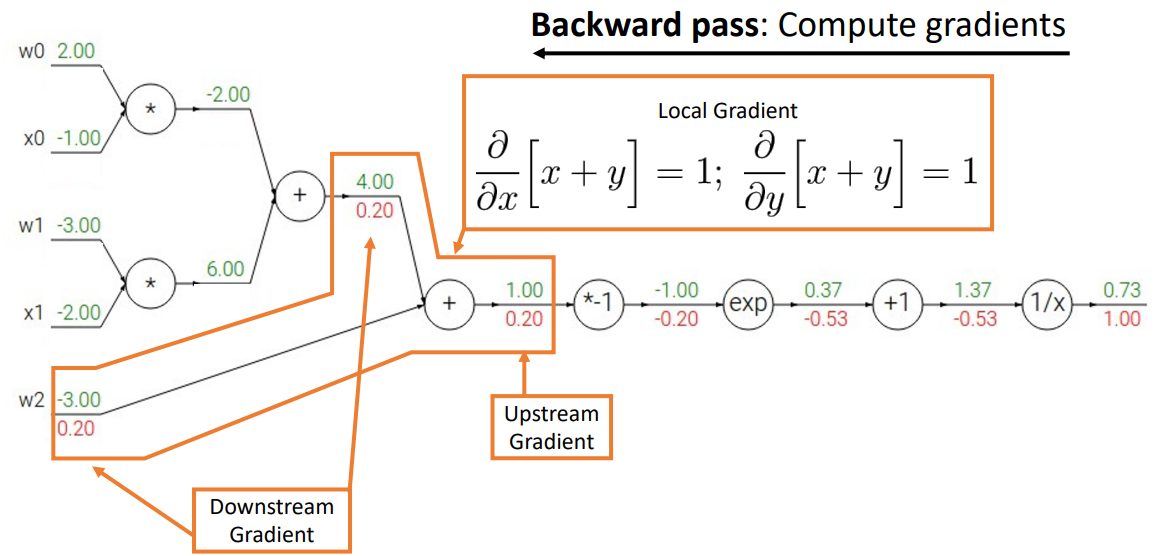
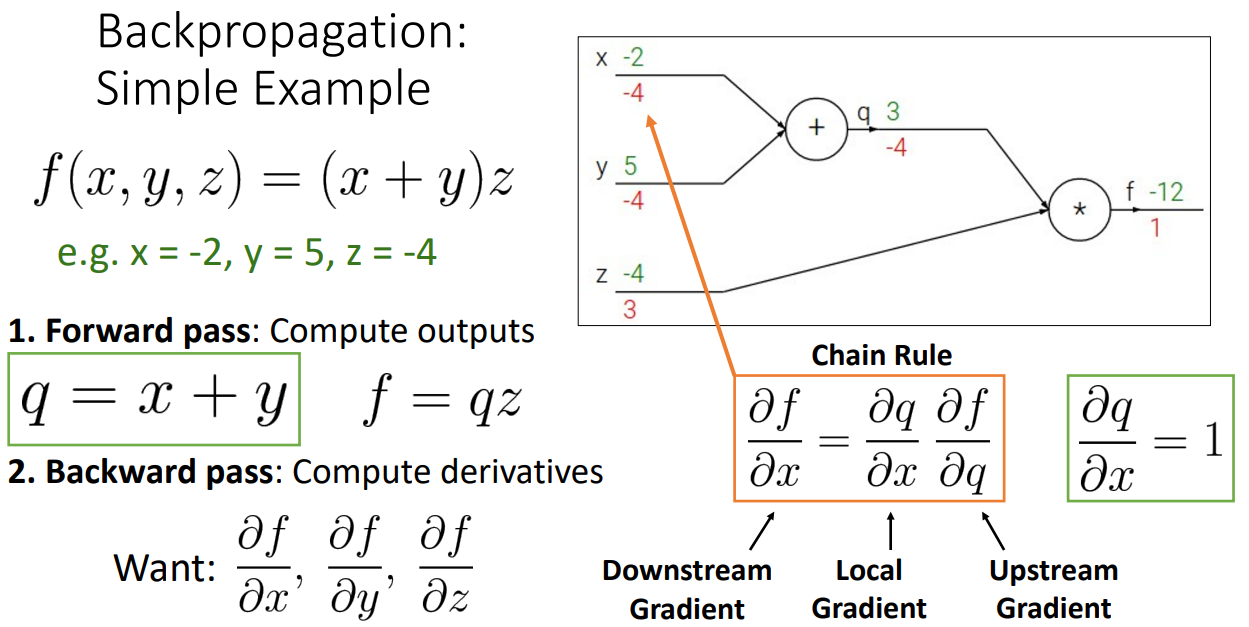
- Step 2. Backward pass
- 모든 출력의 derivatives(gradient)를 계산
- upstream gradient, local gradient를 chain rule을 활용하여 downstream gradient를 구함
ex)
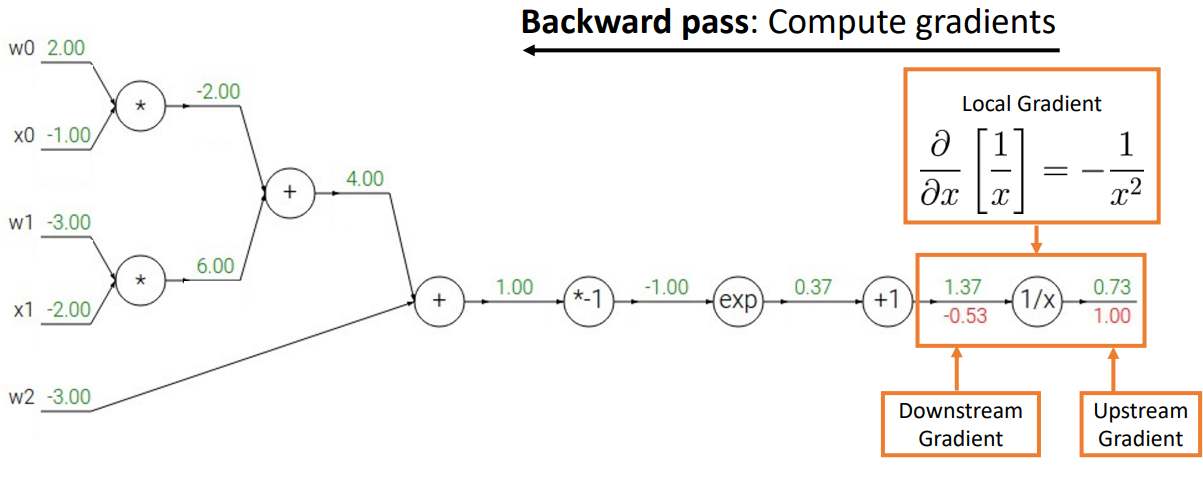
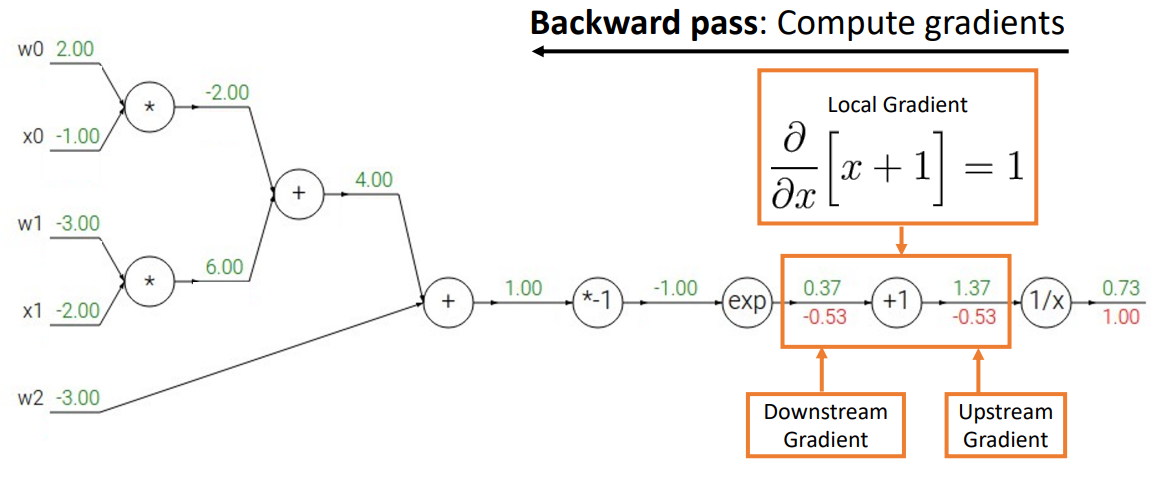
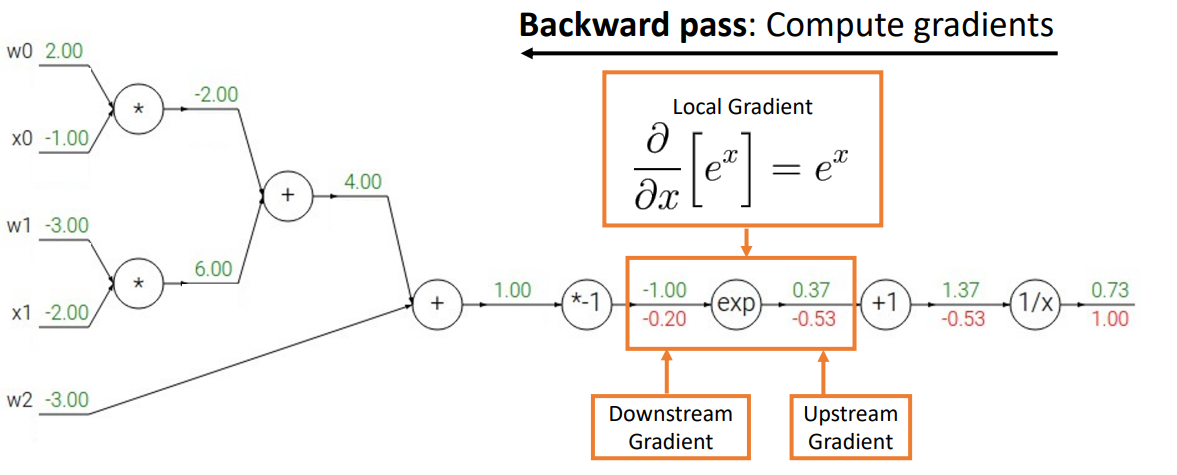
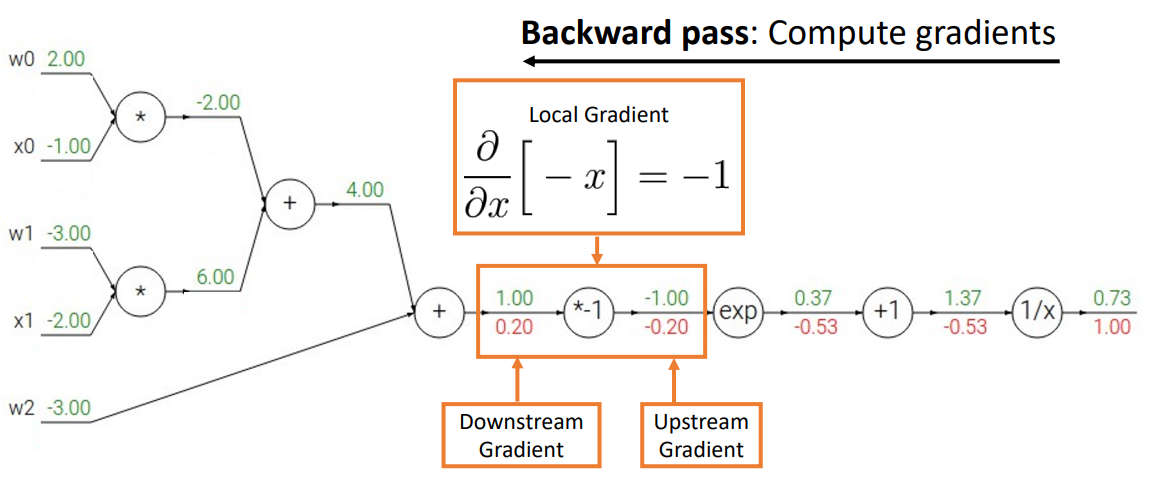
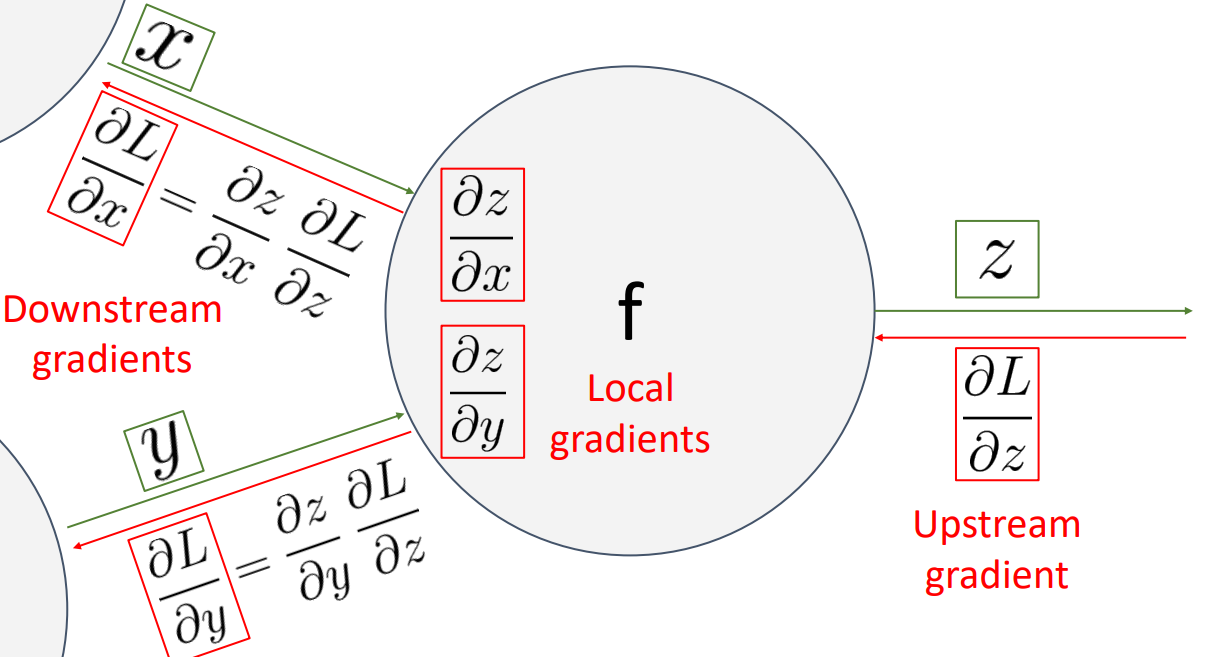
- One node
- 모든 노드가 어떻게 연결되어 있는지 추적하는 구조로, 그래프의 각 노드 내부에서 무슨 일이 일어나고 있는지 지역적으로 생각하고 데이터를 얻기만 하면 됨
- Downstream gradient = Local gradient * Upwnstream gradient
- 프로세스가 끝나게 되면 그래프의 모든 입력과 관련하여 손실의 gradient를 계산한 상태로 남게 됨
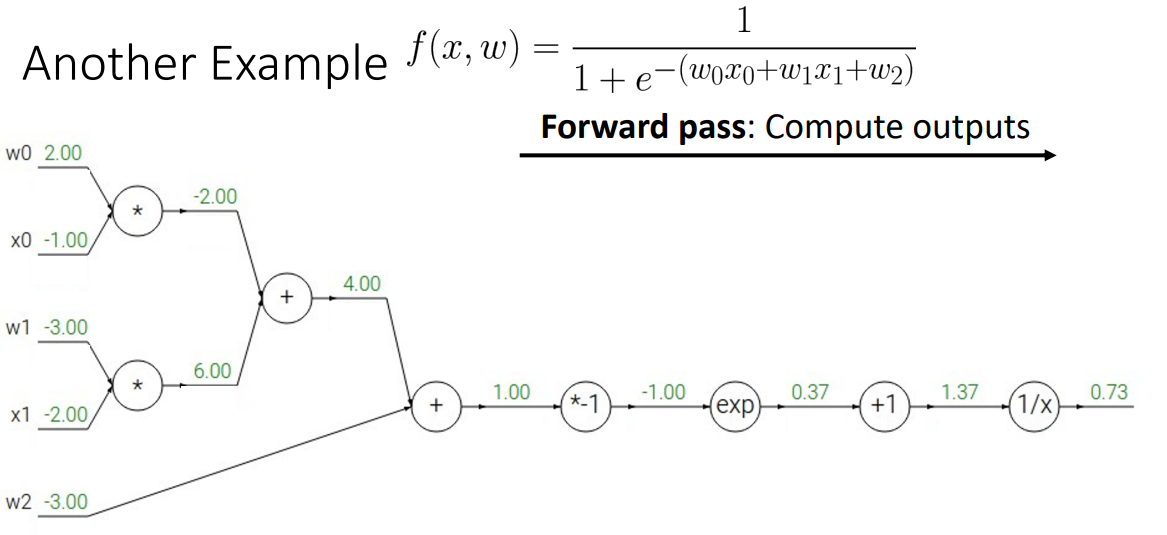
2. Another example
기본적인 산술연산의 관점
- Step 1. Forward pass
- Step 2. Backward pass
- base case부터 구하기
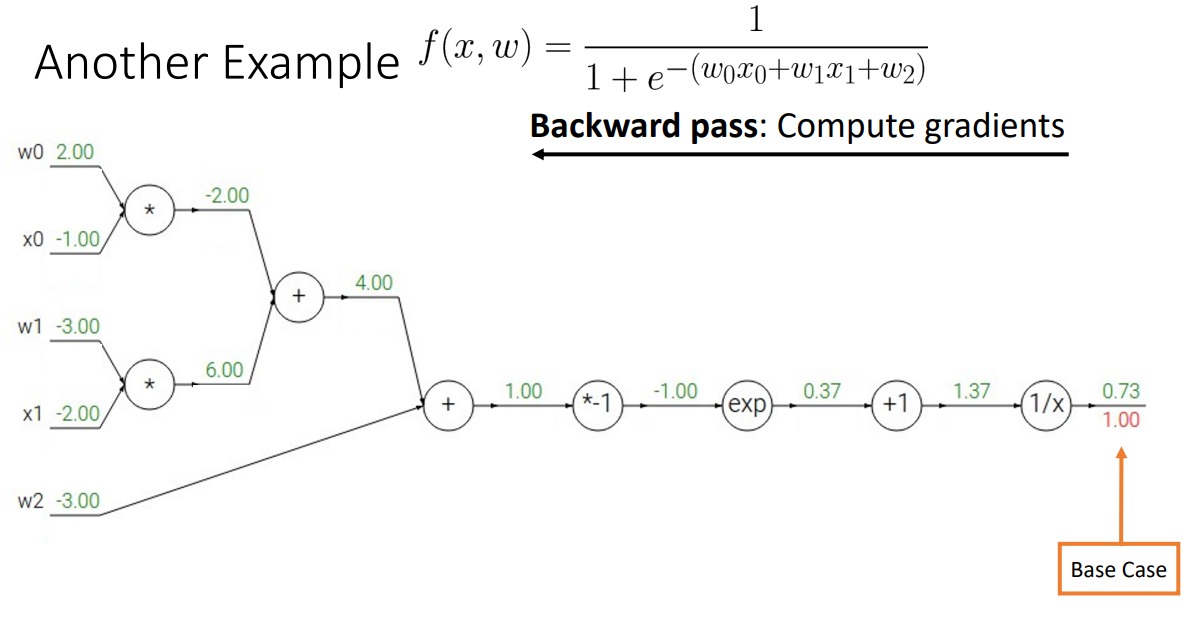
- 한 번에 한 노드씩 뒤로 이동하면서 gradient 계산하기
- base case부터 구하기
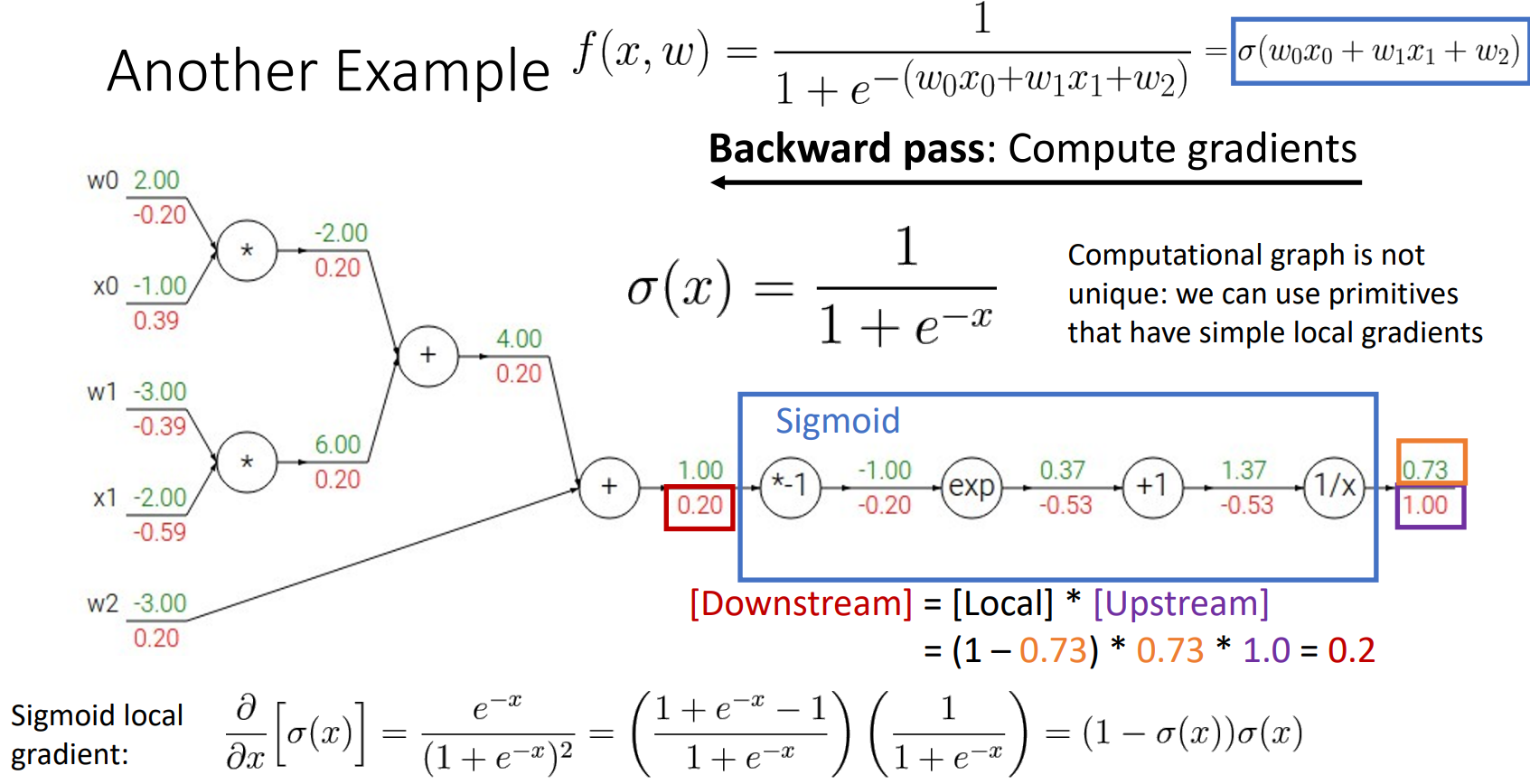
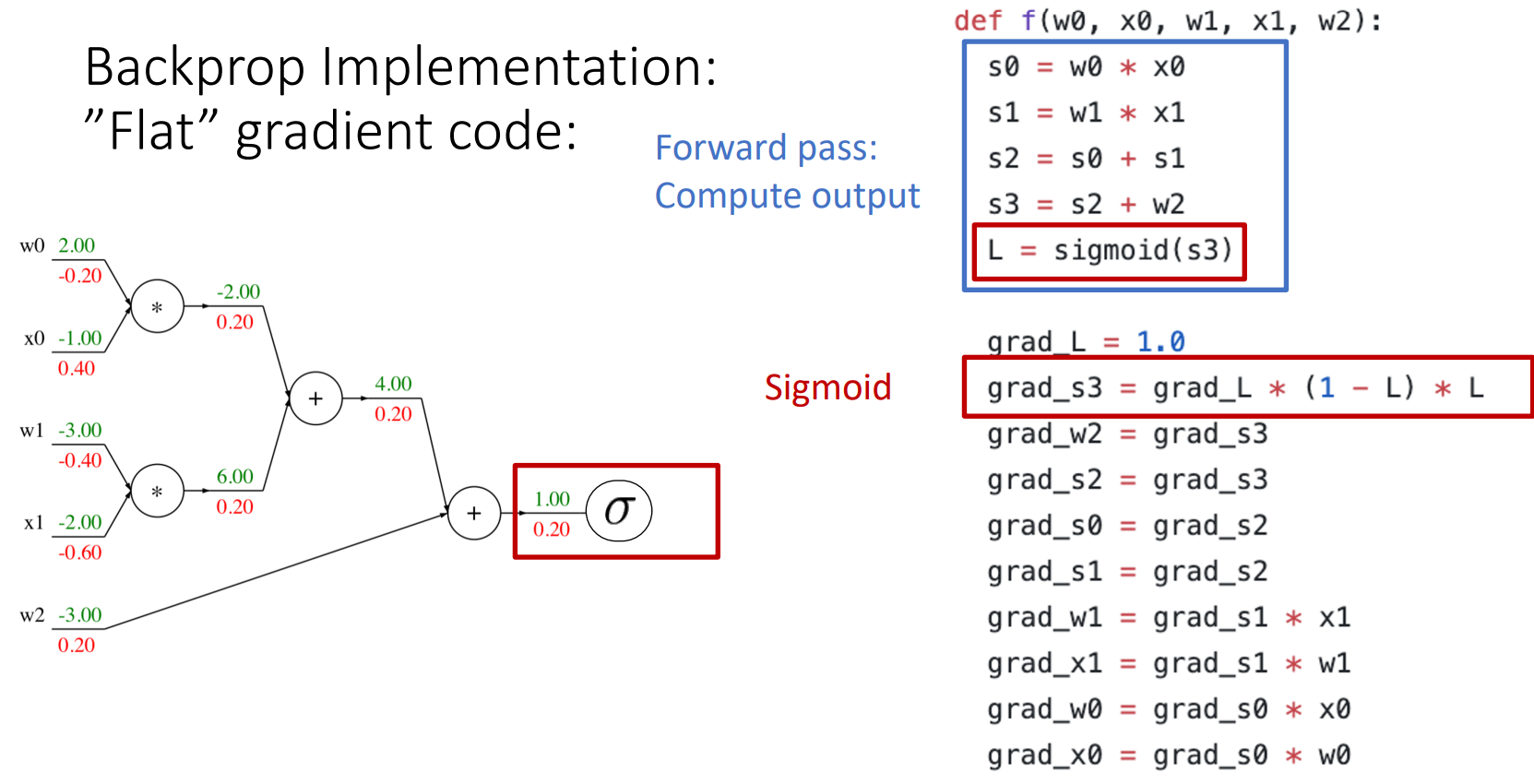
sigmoid로 연산
- backward process를 진행할 때 하나씩 하는 것이 아니라 선택할 수 있는 기본 계산 그래프 요소(ex) sigmoid)를 골라 쉽게 연산을 처리할 수 있음
3. Patterns in Gradient Flow
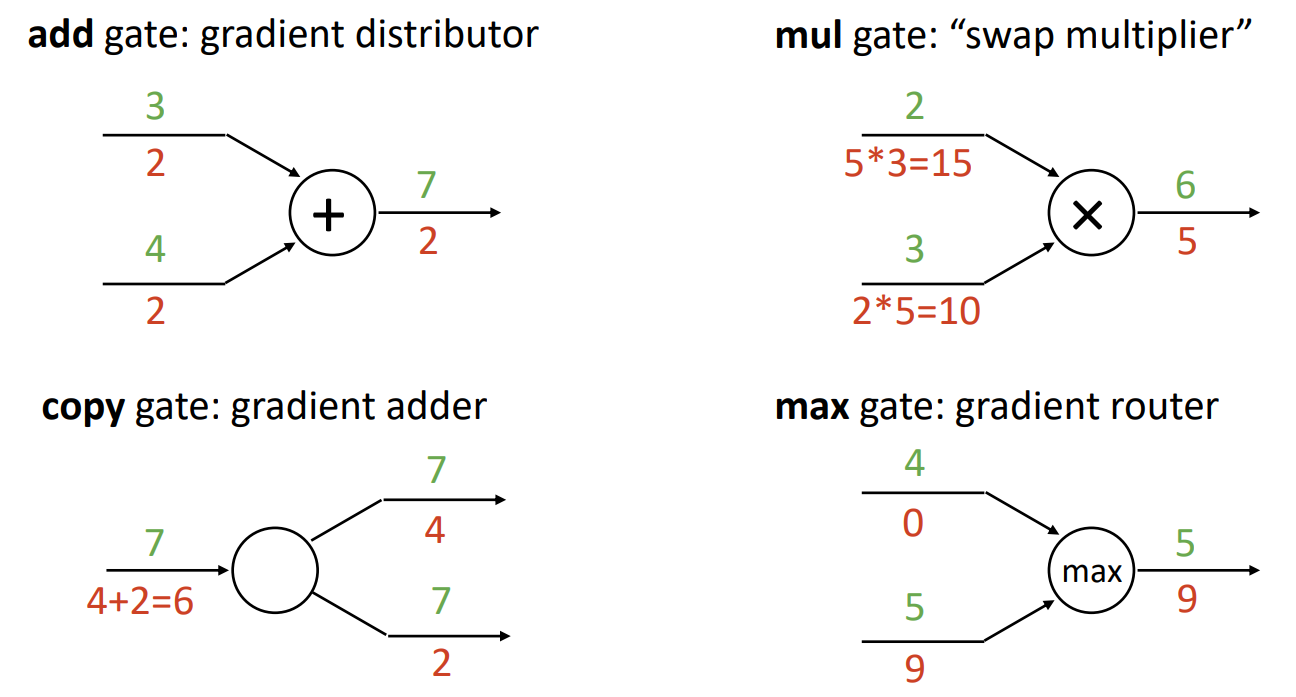
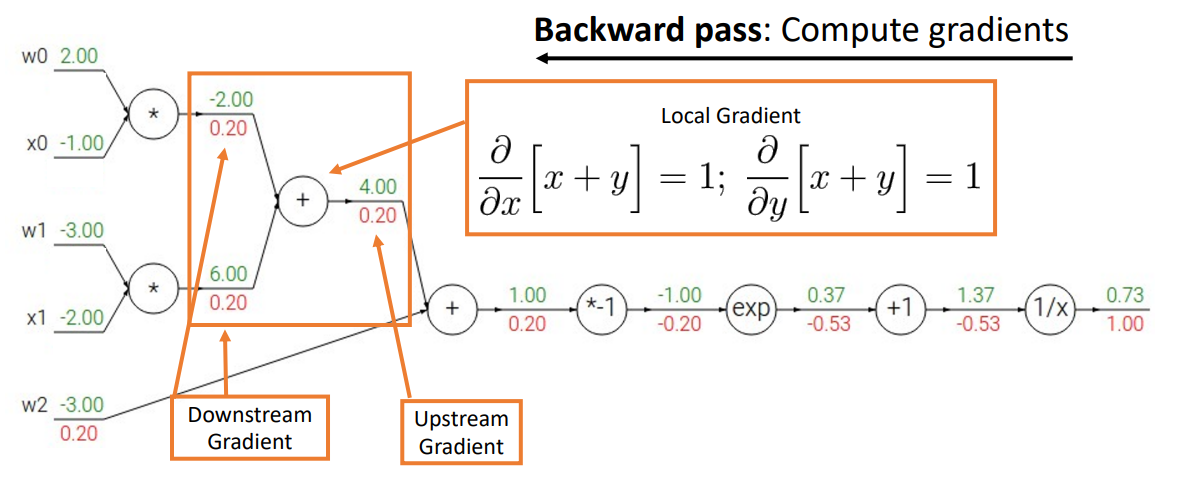
- add gate
- gradient distributor의 역할 (forward: 더하기, backward: 동일한 gradient 분배)
- copy gate
- 도입하는 이유: 동일한 값을 서로 다른 방식으로 사용해야 하는 경우, 다양한 downstream을 처리할 수 있기 위해서
- gradeint adder의 역할 (forward: 복사, backward: gradient 더하기)
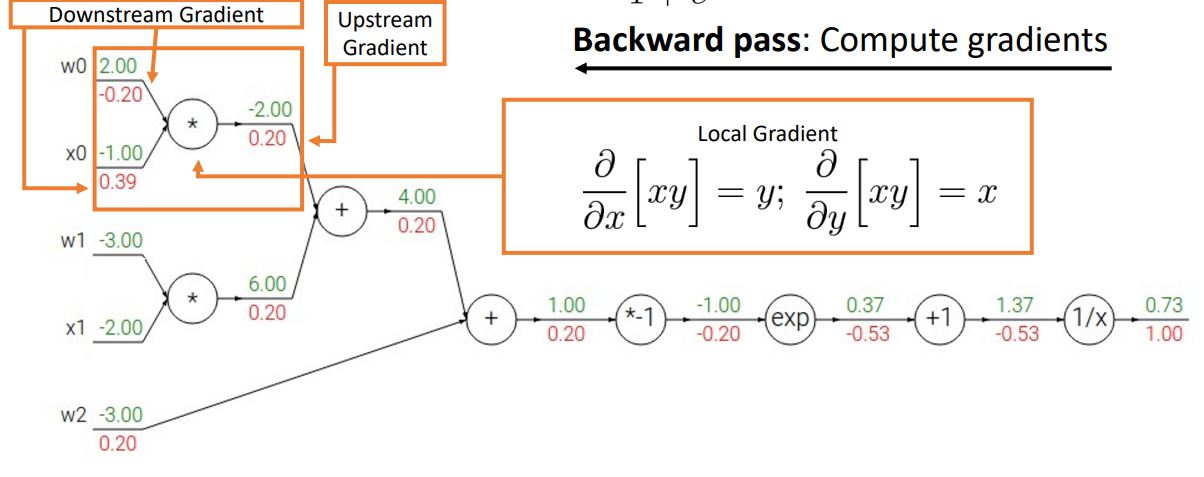
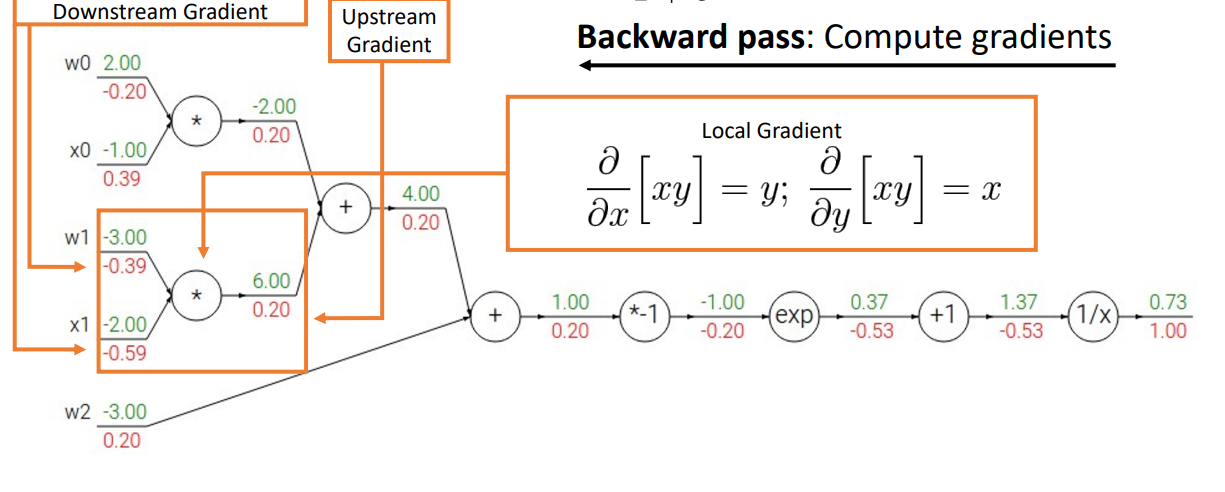
- mul gate
- swap multiplier의 역할 (forward: 곱하기, backward: x, y 각 값을 swap해서 곱하기)
- max gate
- ReLU 함수와 비슷
- gradient router의 역할 (forward: 최댓값, backward: 더 큰 쪽에 gradient 부여하고, 작은 쪽은 0 값 부여)
- 최대값이 아닌 다른 모든 입력에서는 대부분이 0의 gradient를 가지게 되어 전체 모델에서 좋은 등급을 얻는 데 문제가 될 수 있으므로 max gate는 잘 사용하지 않음
4. Backprop Implementation: "Flat" gradient code
- forward pass: output을 계산
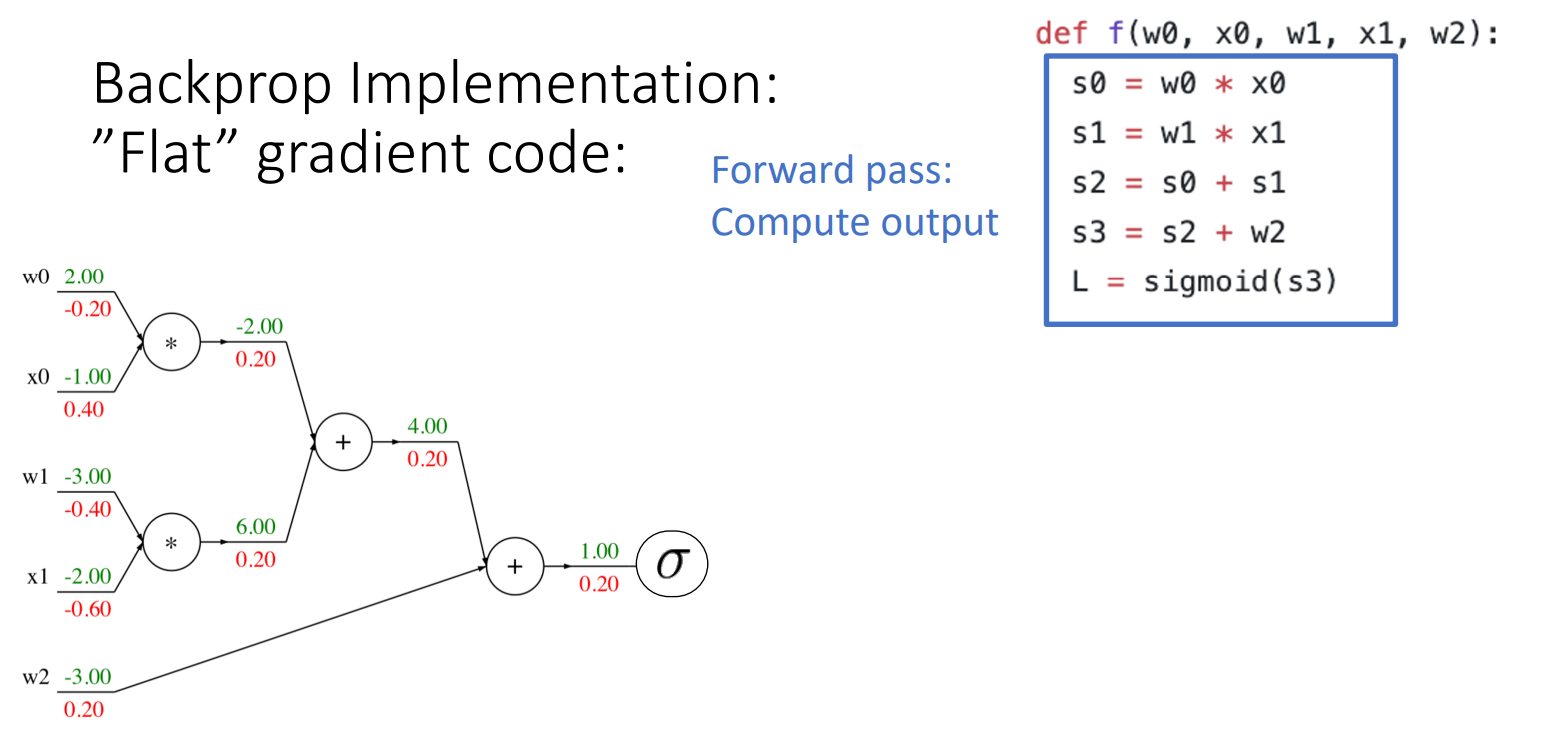
- backward pass
- base case
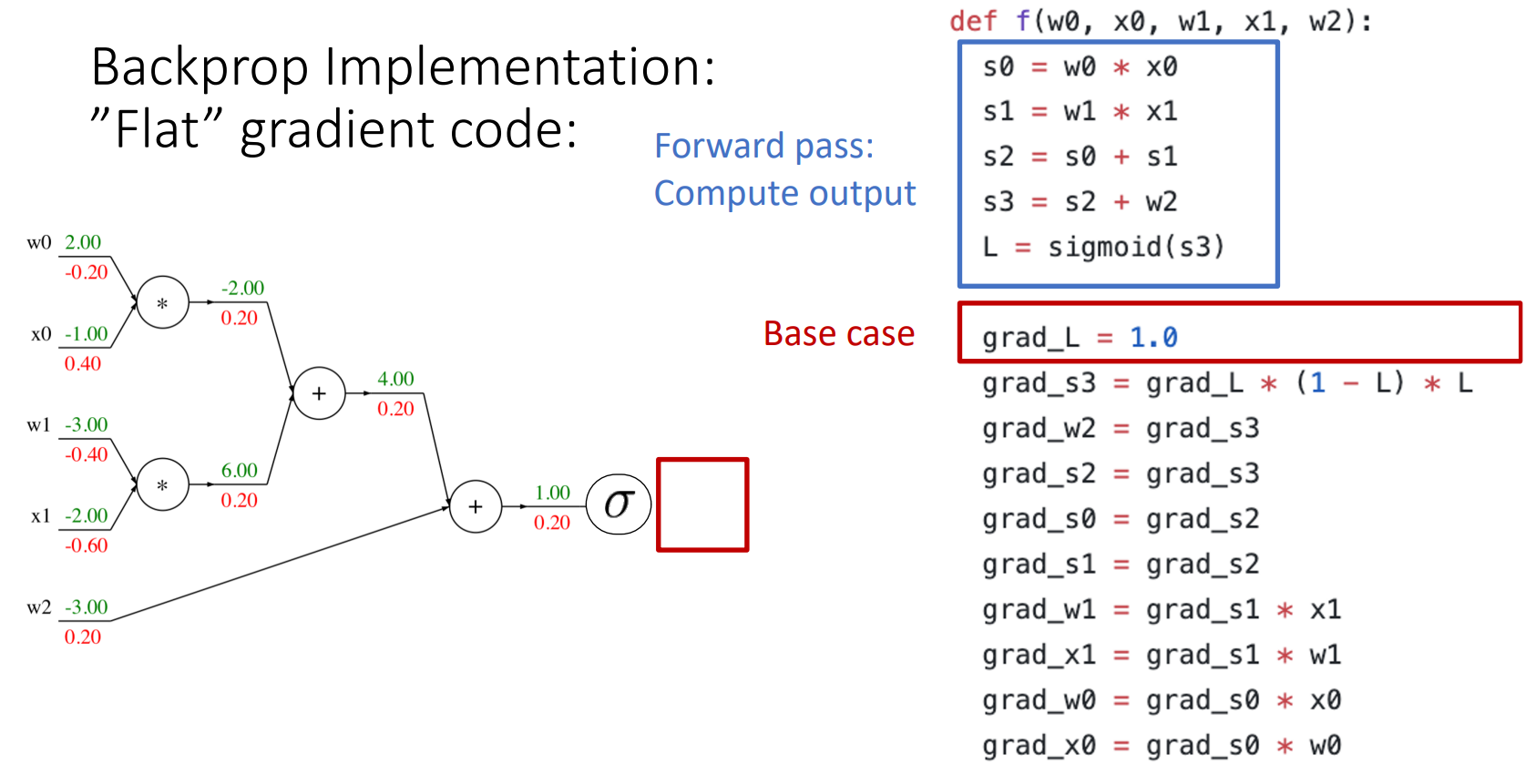
- sigmoid
- add gate
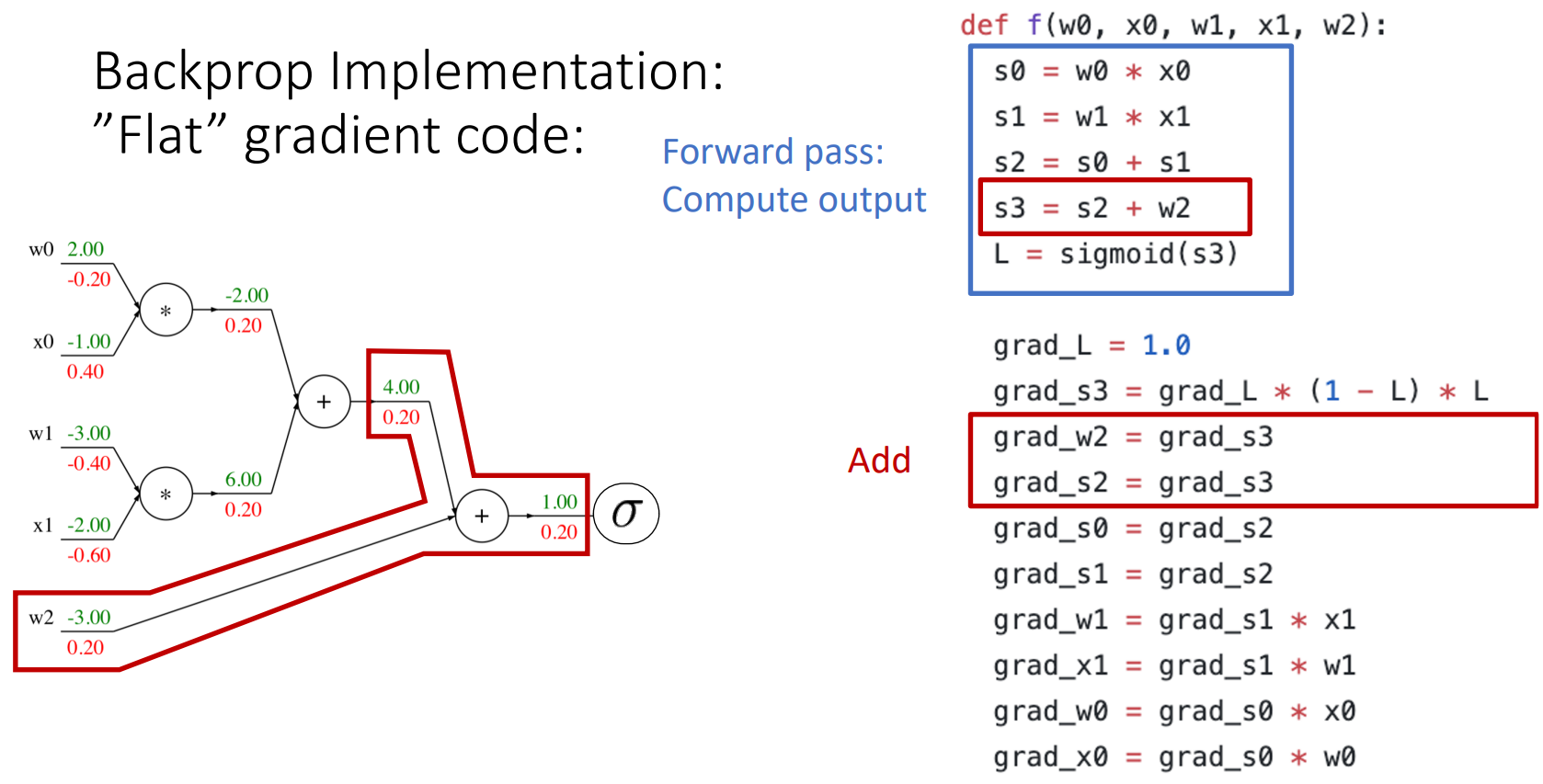

- mul gate
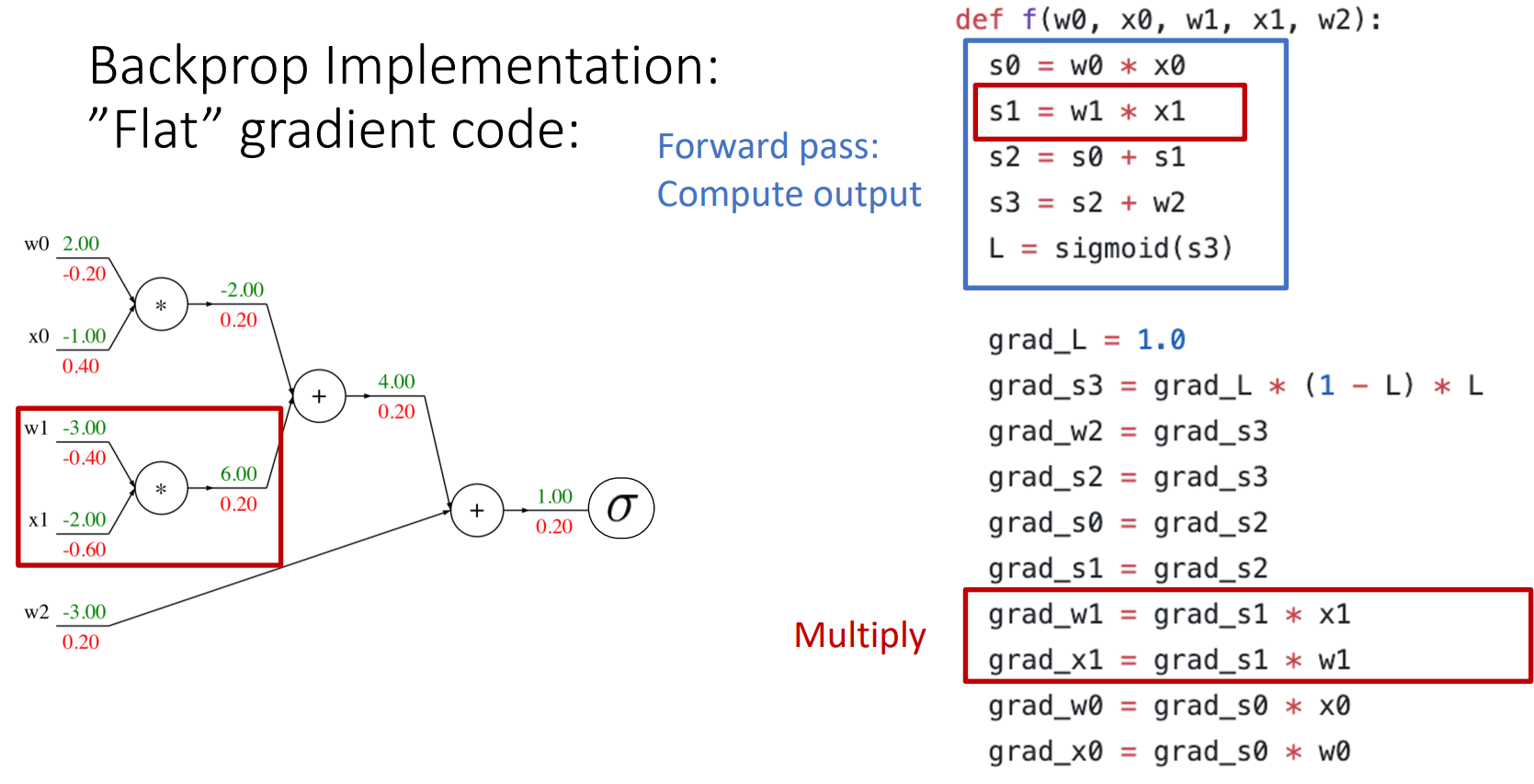
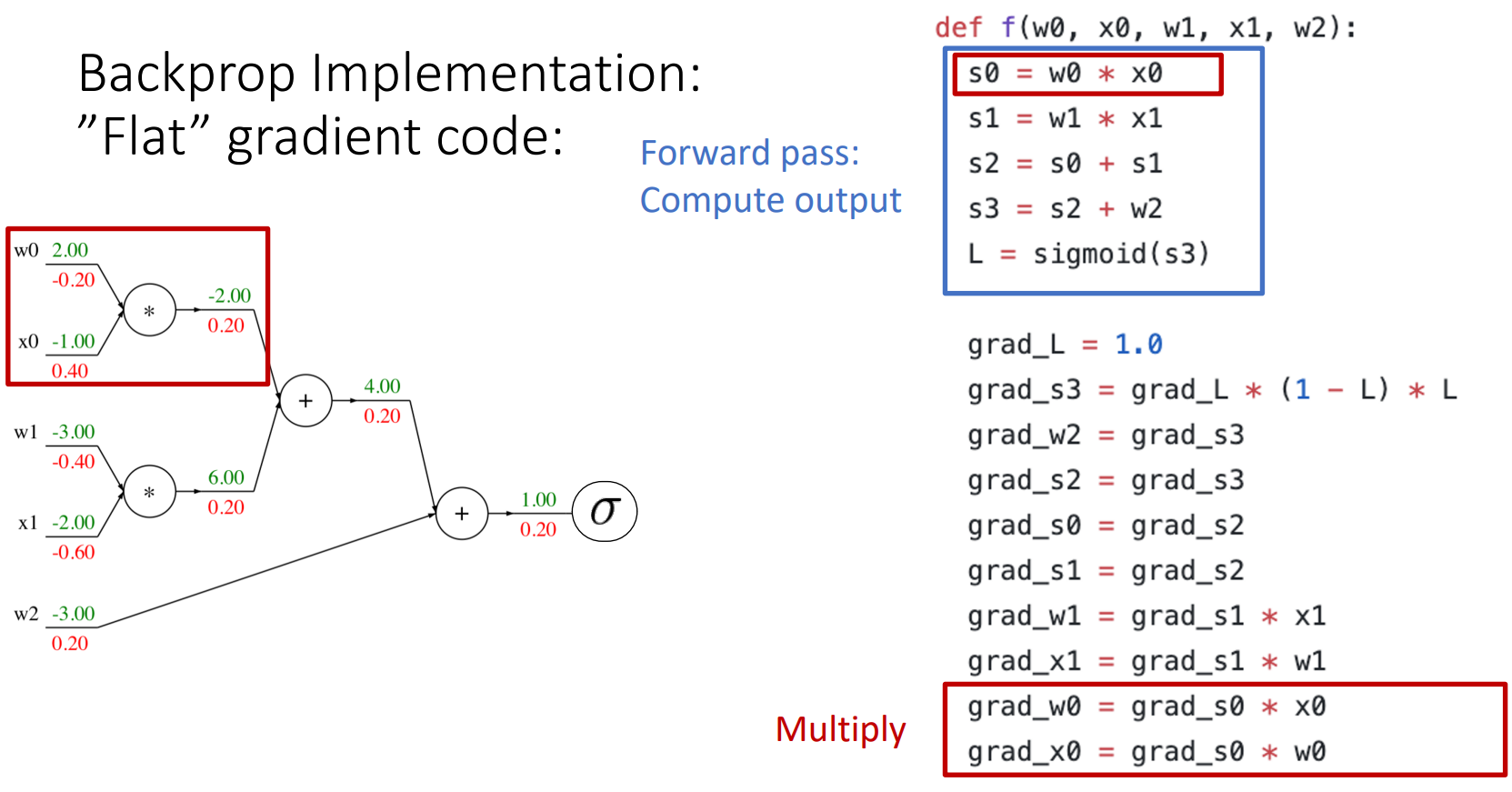
- base case
5. Recap: Vector Derivatives

- x, y 모두 단일값, 스칼라
- regular derivative(일반 미분), x가 변하면 y는 얼만큼 변화하는가?
- x가 벡터, y는 스칼라
- gradient, 각 요소 x의 변화에 y는 얼만큼 변화하는가?
- x, y 모두 벡터
- jacobian, 각 요소 x의 변화에 각 요소 y에 미치는 영향
6. Backprop with Vectors
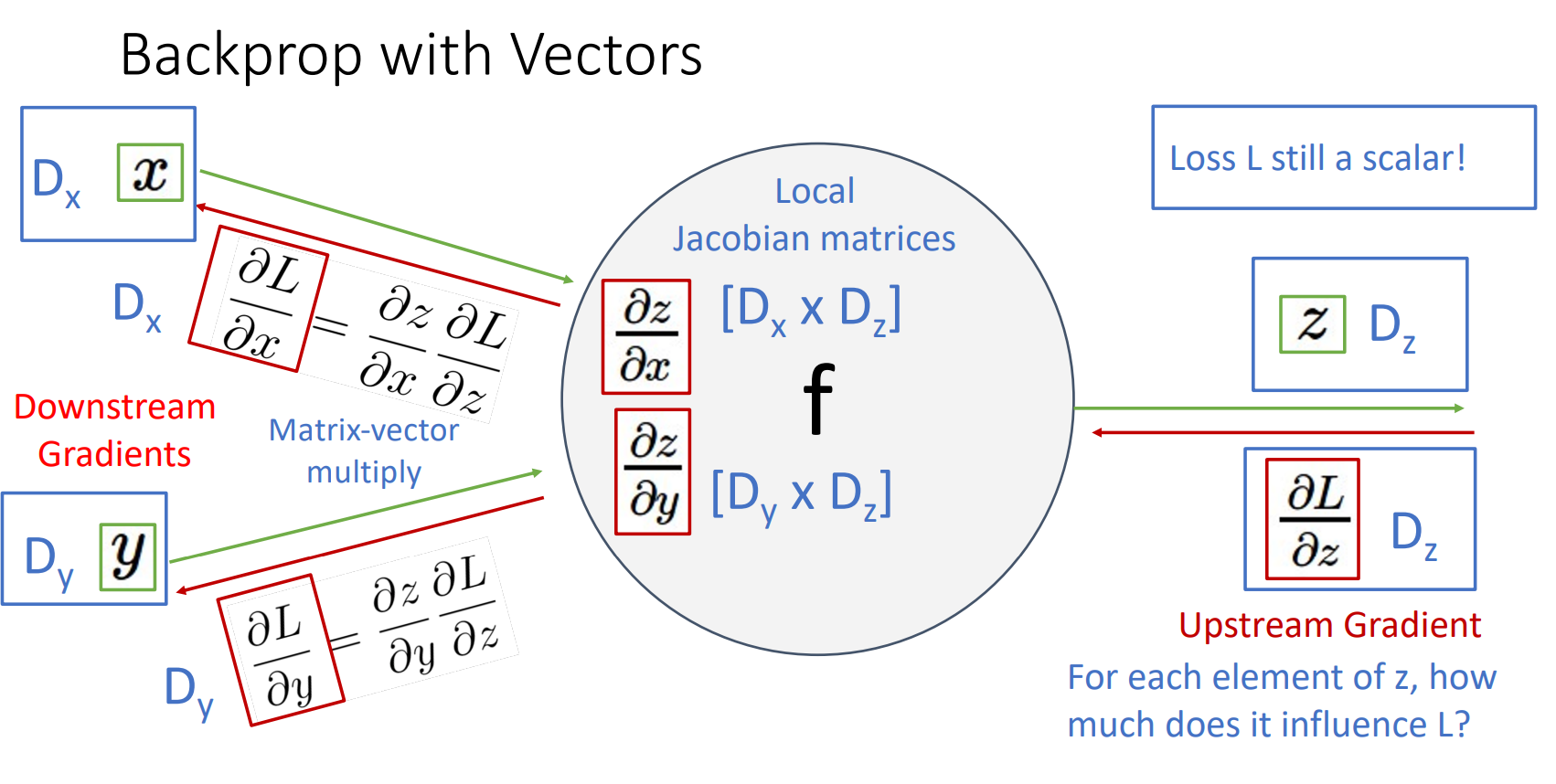
- Upstream gradient
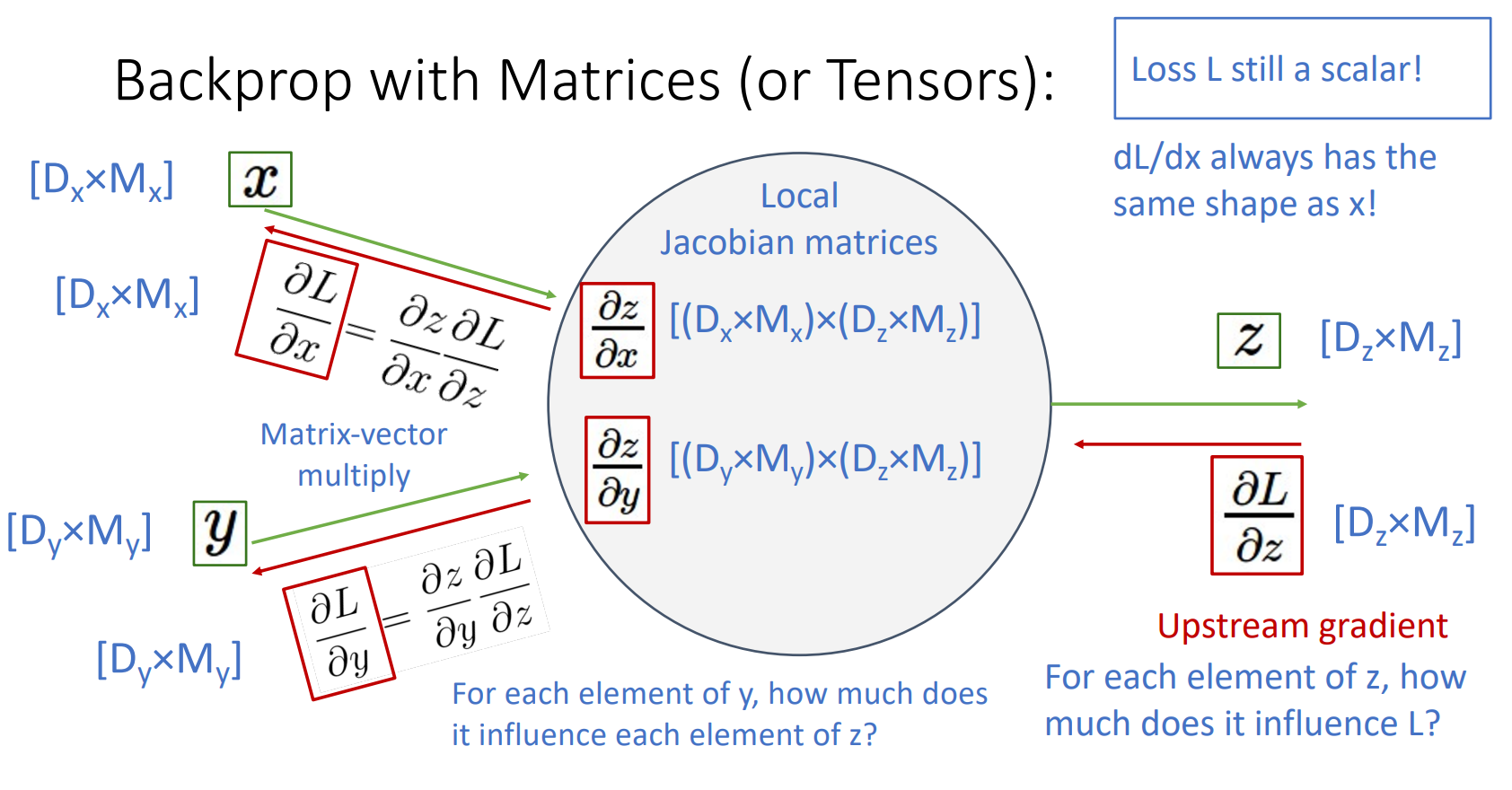
- L은 항상 scalar임
- 각 요소 z가 변하면 L은 얼마나 변화하는가?
- Local gradient
- x, y, z 모두 벡터이므로 Local jacobian matrices가 됨
- 각 입력 요소인 x, y가 변하면 z는 얼마나 변화하는가?
- Downstream gradient
- Downstream = Local * Upstream
- 예시 (ReLU function)
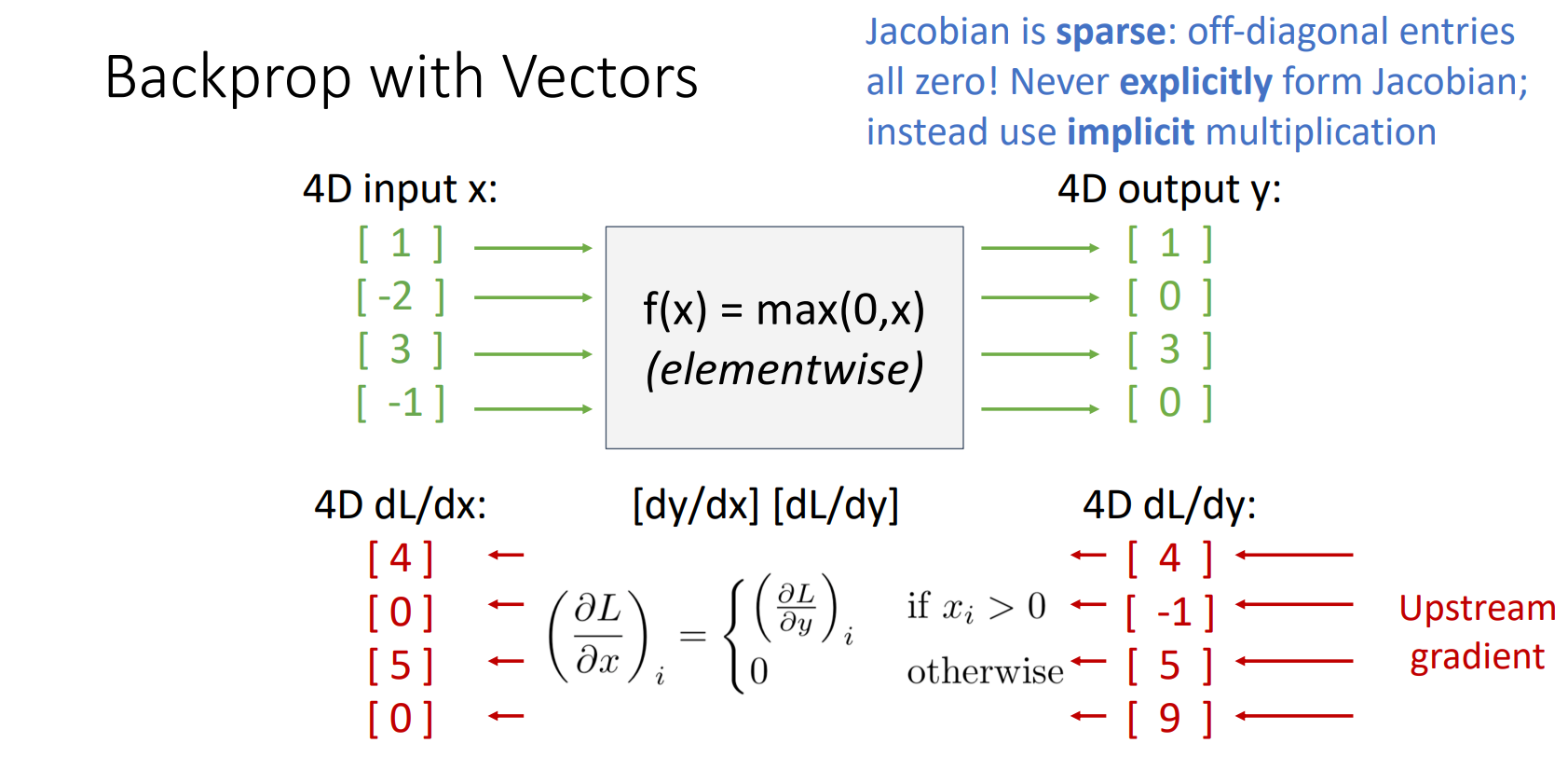
- Upstream
- output y에 의해 L이 얼마나 변화하는가?
- Local
- Jacobian이 Sparse(희소)하다: ReLU의 미분값은 0 또는 1이므로, Jacobian 행렬은 대각선 요소만 1 또는 0이며 나머지는 모두 0임
- 0 값이 많은 Jacobian 행렬을 명시적으로 만들고 계산하는 것은 비효율적이기 떄문에 이 곱셈을 암시적으로 수행하는 것이 효율적임
- Downstream
- 암시적 구현 방법: upstream 값에 ReLU 함수 적용하면 Upstream 값 얻을 수 있음
- Upstream
7. Backprop with Matrices (or Tensors)
8. Example: Matrix Multiplication
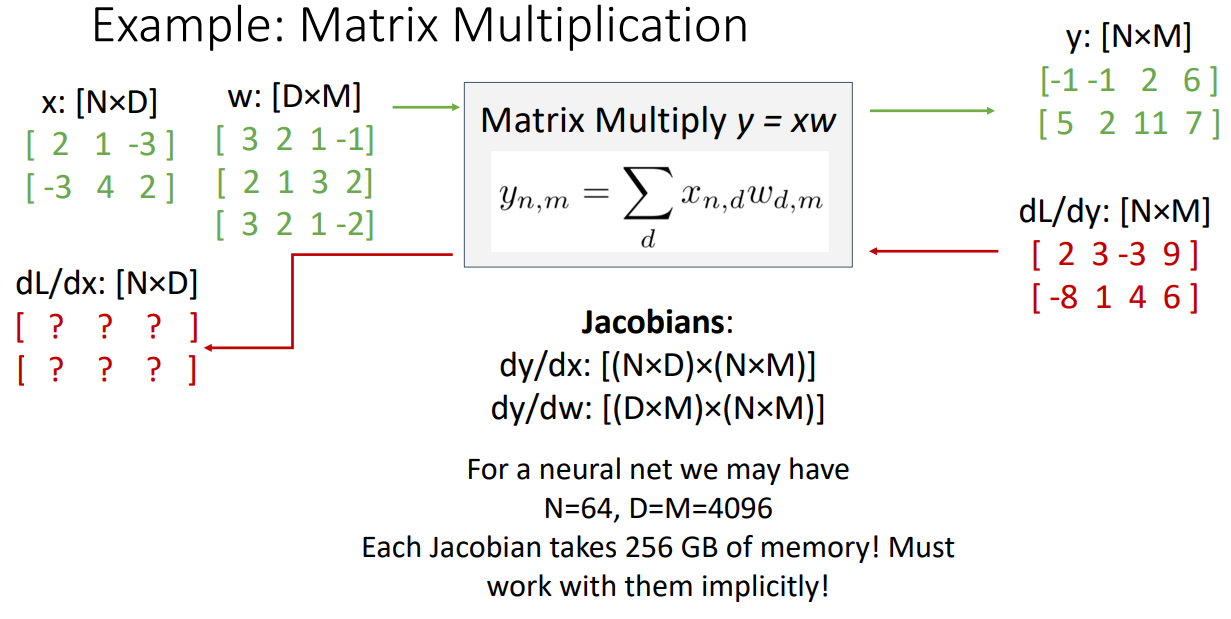
-
dL/dy: [NxM] = Y의 각 요소가 최종 보스 L에 얼마나 영향을 미치는가? 임의의 값
-
dy/dx: [(NxD)x(NxM)] / dy/dx:[(DxM)x(NxM]: Jacobians, 차원에 따라 값이 급격하게 커지므로 명시적으로 야코비안을 형성하는 것은 옳지 않고, 이를 암묵적으로 수행할 방법을 찾아야 함
-
입력의 한 요소인 단일 스칼라 에 대해 생각해보기
- dy/d = 스칼라 입력 요소 에 대한 출력 행렬 y의 미분



- dL/d = dy/d * dL/dy

- 모든 요소를 위와 같이 구하기

- 야코비안 행렬 형성 없이 암묵적인 방법으로 식 구하기: dL/dx = (dL/dy)
- 이 값은 실제로 고차원 희소 야코비안 행렬과 Upstream gradient 사이의 암묵적 행렬 벡터의 곱

- 이 값은 실제로 고차원 희소 야코비안 행렬과 Upstream gradient 사이의 암묵적 행렬 벡터의 곱
- dy/d = 스칼라 입력 요소 에 대한 출력 행렬 y의 미분
9. Backpropagation: Another View
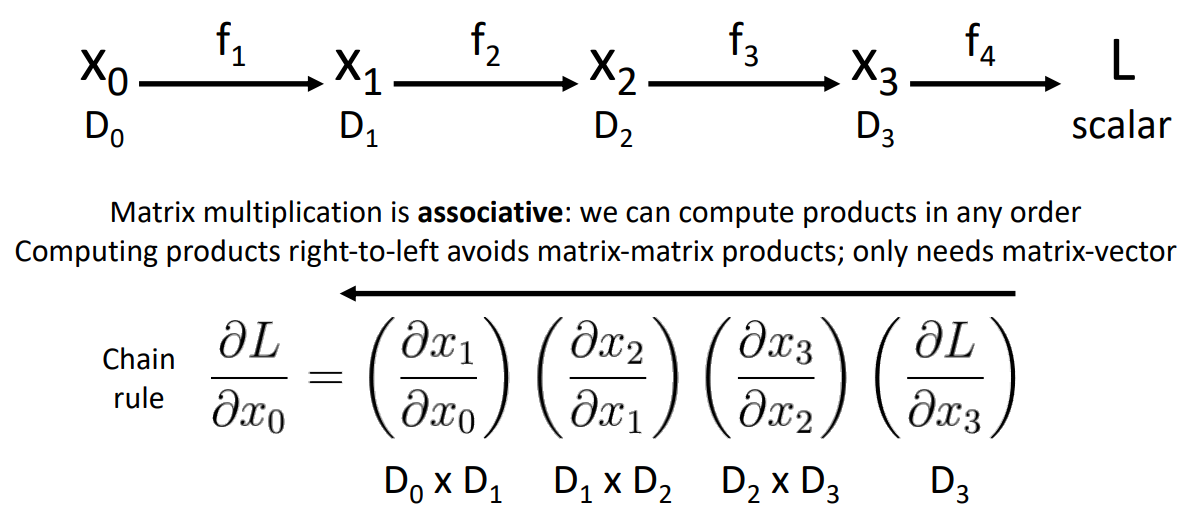
- Chain rule: 연쇄 법칙을 활용하여 출력에서 입력으로 그래디언트를 전파하는 과정
- 행렬 계산은 연쇄적이며 결합 법칙을 따르므로 계산 순서를 어떤 순서로도 계산할 수 있음
- right-to-left로 역방향 계산을 진행하면 matrix-matrix 계산이 아닌 matrix-vector 계산이 가능하여 연산량이 줄어듦
10. Automatic Differentiation (자동 미분)
- Reverse-Mode Automatic Differentiation
- 오른쪽에서 왼쪽으로 가는 방식으로 야코비안 행렬을 곱하는 해석 때문에 역전파는 Reverse-Mode Automatic Differentiation라고 불림

- 오른쪽에서 왼쪽으로 가는 방식으로 야코비안 행렬을 곱하는 해석 때문에 역전파는 Reverse-Mode Automatic Differentiation라고 불림
- Forward-Mode Automatic Differentiation
- 스칼라 입력값을 갖고 스칼라 입력 값의 미분을 구한 다음 왼쪽에서 오른쪽으로 곱셈을 수행

- 스칼라 입력값을 갖고 스칼라 입력 값의 미분을 구한 다음 왼쪽에서 오른쪽으로 곱셈을 수행