Graph

알고리즘의 꽃이자 코테의 단골 손님인 그래프이다.

세상엔 참 많은 종류의 그래프가 있다.

우리는 이를 이용하여 문제를 해결하려고 한다.

어떤 문제냐고?

1. 최단 거리 구하기
2. 위상 정렬
3. SCC(Strongly Connected Components) 찾기

당연히 뭔지 잘 모르겠지.

하나하나 알아가봅시다.

Undirected Graph

일단 그래프에도 종류가 있는데 먼저 무방향 그래프부터 알아보자.

아래는 무방향 그래프를 그림으로 나타낸 예시이다.

그림 같은 경우에는 정말 당연하게도 화살표가 없다. (無방향 그래프니까!)

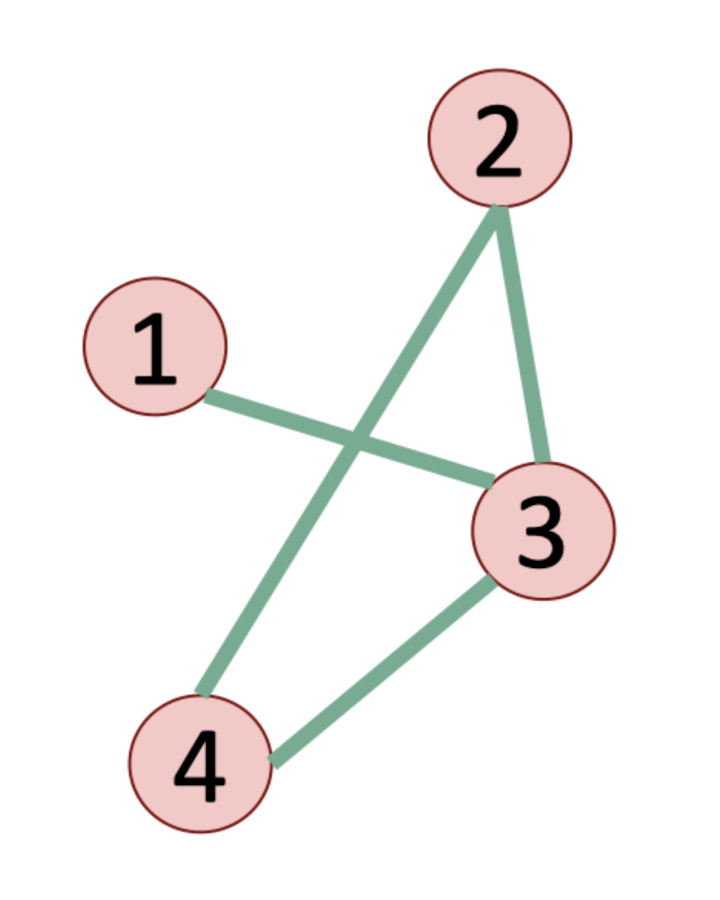
기본적으로 그래프는 알파벳 $G$ 로 나타낸다.

저기 숫자 적힌 동그라미들을 우리는 정점 이라고 부를 거고, 영어로는 vertex 라고 한다.

그럼 정점들의 집합은 뭘로 나타낼까?

맞다. 알파벳 $V$로 나타낸다.

그리고 초록선들은 간선 이라고 부를거고, 영어로는 edge 라고 한다.

프로출신들은 한 번에 알겠지만 당연하게도 알파벳 $E$로 나타낸다.

그래서 저 그래프를 예시로 정리를 해주면,

$G = (V,E)$
$V = {1, 2, 3, 4}$
$E = {(1,3), (2,4), (3,4), (2,3)}$

으로 나타낼 수 있겠다.

그리고 degree와 neighbor이라는 용어가 등장하는데 각각 정점에 연결된 간선의 개수, 그리고 바로 연결되어 있는 정점의 개수를 나타낸다.

4를 기준으로 degree는 2이고, neighbor는 2와 3이다.

Directed Graph

무방향 그래프가 있다면 당연히 방향 그래프도 존재한다.

직관적으로 화살표까지 그려주는 아주 친절한 그래프이다.

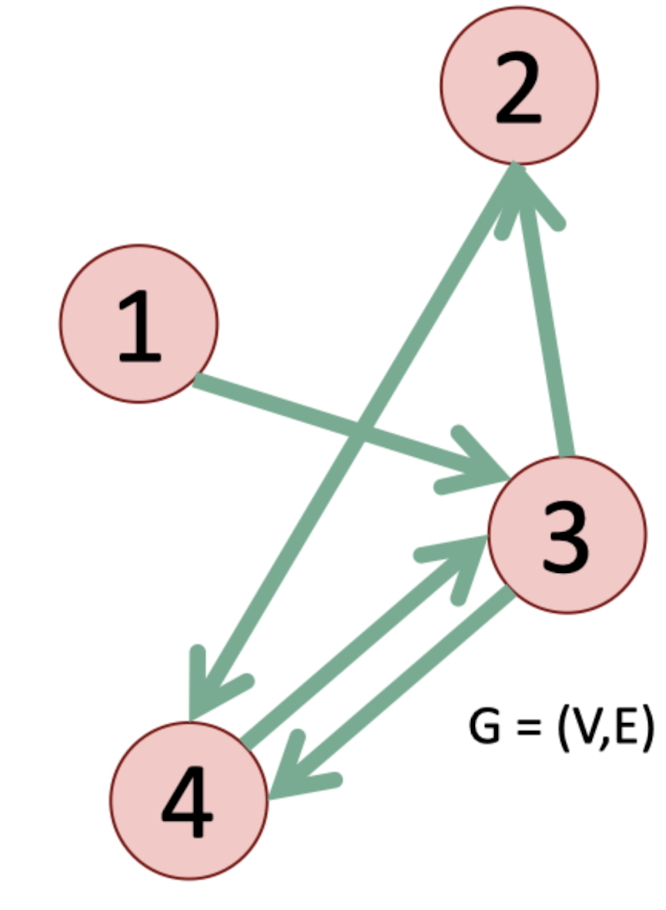
물론 그래프 그래프 표현 방법은 달라질 것이 없다.

다만 edge의 표현 방법이 살짝 다른데, 원래는 (3, 4) 라고 하면 3과 4를 잇는 하나의 edge를 나타냈다면, 방향 그래프에서는 3에서 4로 가는 edge만을 나타내고, 4에서 3을 가는 것은 포함하지 않는다는 것이다.

이건 헷갈리지 않도록 주의하자.

방향이 생긴만큼 degree와 neighbor도 구분이 생긴다.

in-degree는 들어오는 간선, out-degree는 나가는 간선이다.

아까랑 같이 예시를 들어보면 4번 기준으로 각각 2개, 1개가 되겠다.

incoming neighbor와 outgoing neighbor로도 나뉘는데, 각각 2, 3과 3이 되겠다.

Represent Graph

이제 이 그래프들을 표현할 방법을 생각해보자.

그냥 그림 그리면 안 되냐고?

나가라.

컴퓨터가 그림을 어케 알아볼건데!!

gpt는 알아본다고?

나가라.

gpt는 뭐 눈이라도 달린 줄 아나.

암튼 컴퓨터가 알아먹게 만들라면 두가지 방법이 존재한다.

Adjacency Matrix

우리말로는 인접 행렬이라고 한다.

세로 축이 시작점이고, 가로 축이 도착점이다.

해당하는 edge가 있으면 1로, 아니면 0으로 나타낸다.

위의 무방향 그래프를 인접 행렬로 나타내면 아래와 같다.

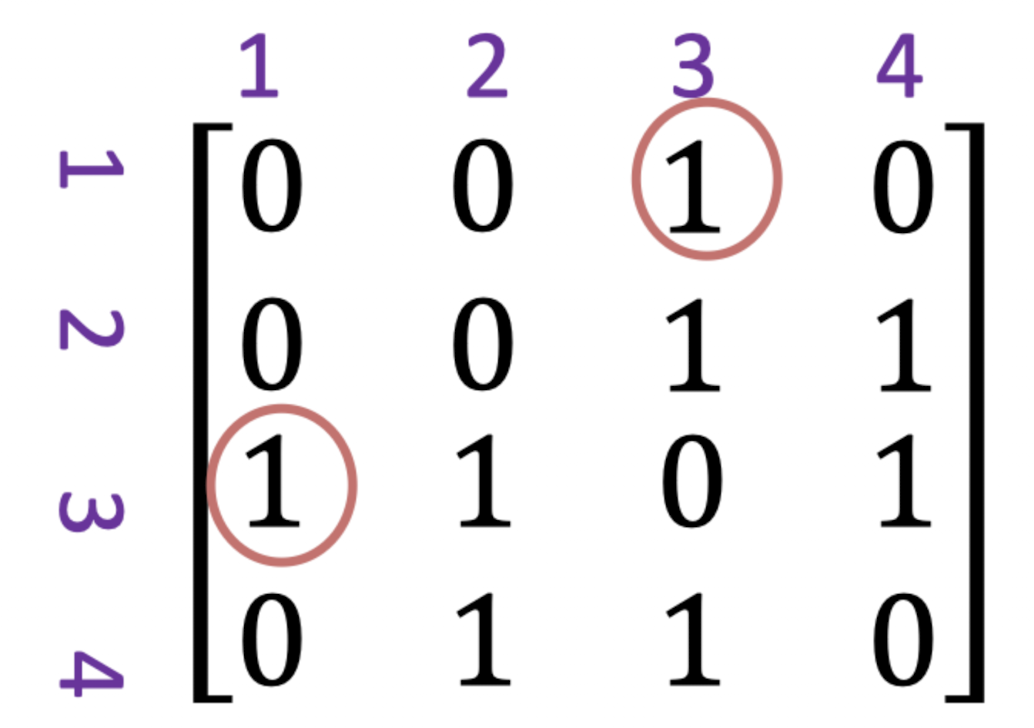
잘 보면 중간에 0 0 0 0을 기준으로 좌하단과 우상단이 대칭인 모습을 볼 수 있는데, 이는 무방향 그래프의 특징이라고 볼 수 있겠다.

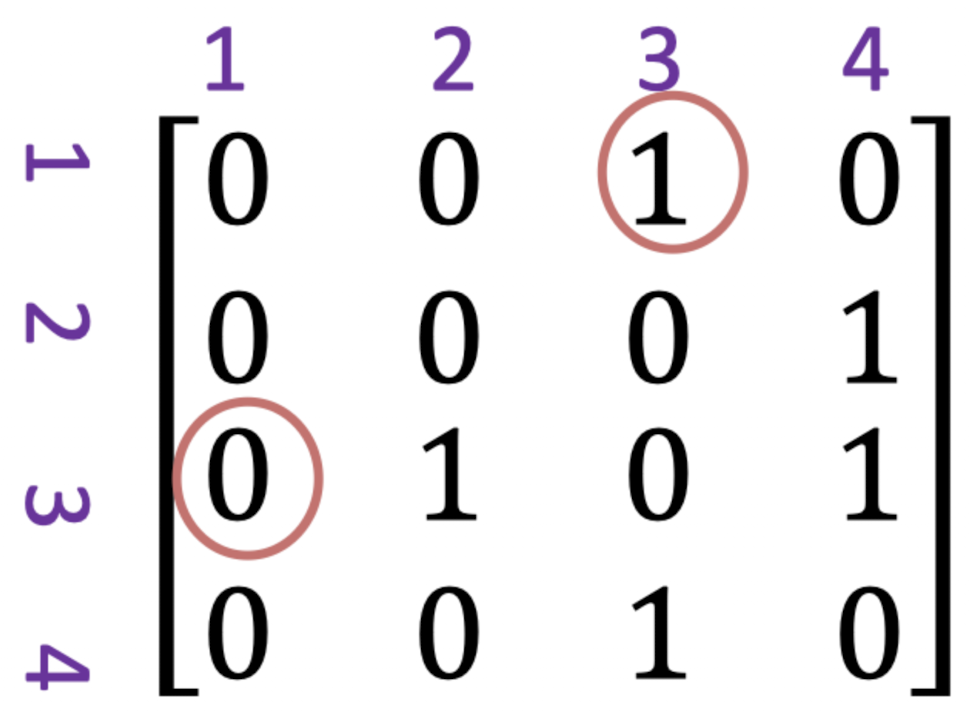
방향 그래프는 위와 같은 생김새를 하고 있다.

대칭은 개나줘버린 모습이다.

Adjacency List

두번째는 인접 리스트이다.

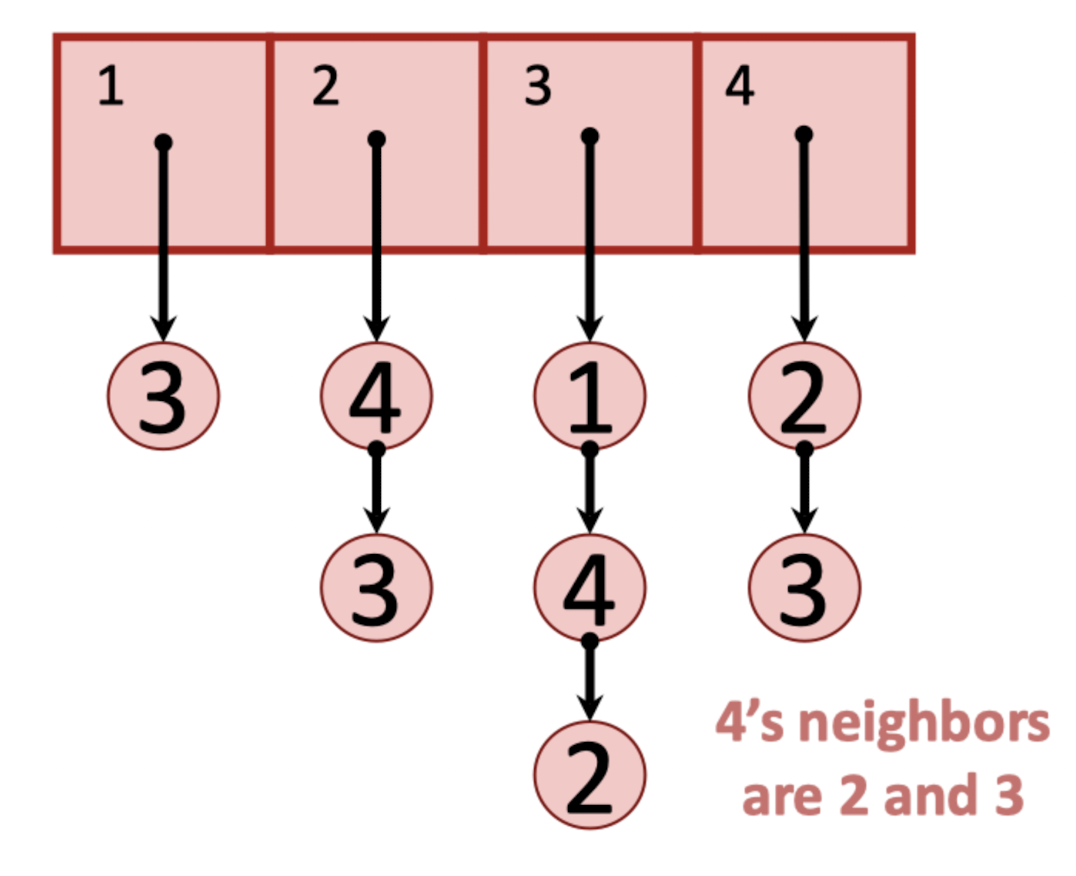
정점마다 공간을 하나씩 할당해주고, 이웃들을 연결해주는 방식이다.

정점 4의 이웃에는 2와 3이 있다고 했었는데, 아래와 같이 잘 들어가있는 것을 볼 수 있다.

Comparision

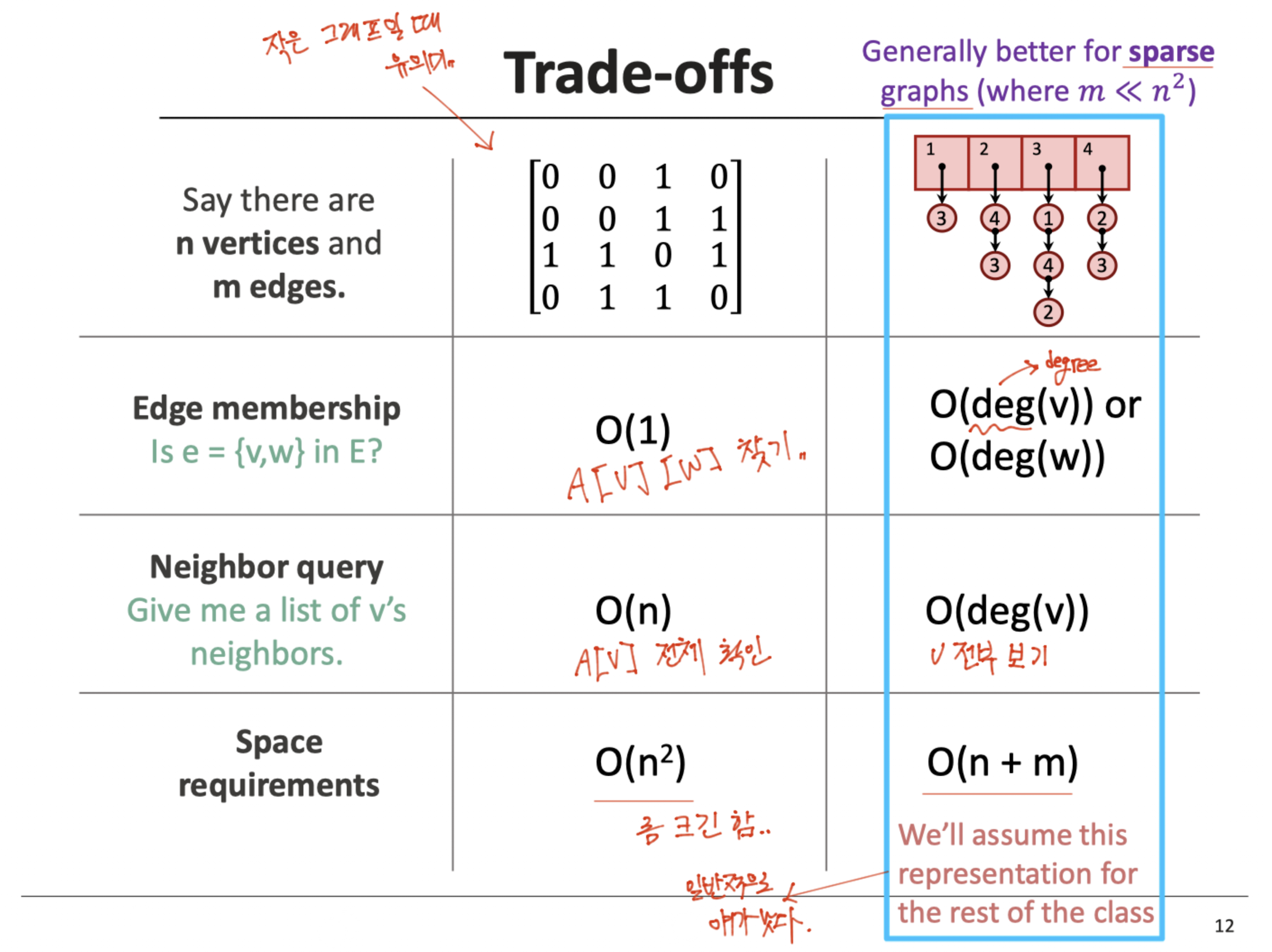
두 개를 비교하면 edge를 찾는 것은 인접 행렬이 유의미할 수 있으나, 전체적으로는 인접 리스트가 좀 더 나은 성능을 보여준다.

특히 공간적인 측면에서 확실히 나은 것이 눈에 보인다.