Hash

직전까지 BST를 통해 Search, Insert, Delete의 연산을 $O(log(n))$ 시간에 할 수 있음을 알게 되었다.

하지만 인간의 욕심은 끝이 없고 이젠 하다하다 상수 시간에 저 작업을 다 할 수 있기를 바란다.

그게 되냐고?

Hash는 가능하게 한다.

마치 Counting Sort처럼 하나의 공간에 하나의 요소를 매핑하면 즉시 즉시 모든 작업을 해낼 수 있다.

Direct Addressing

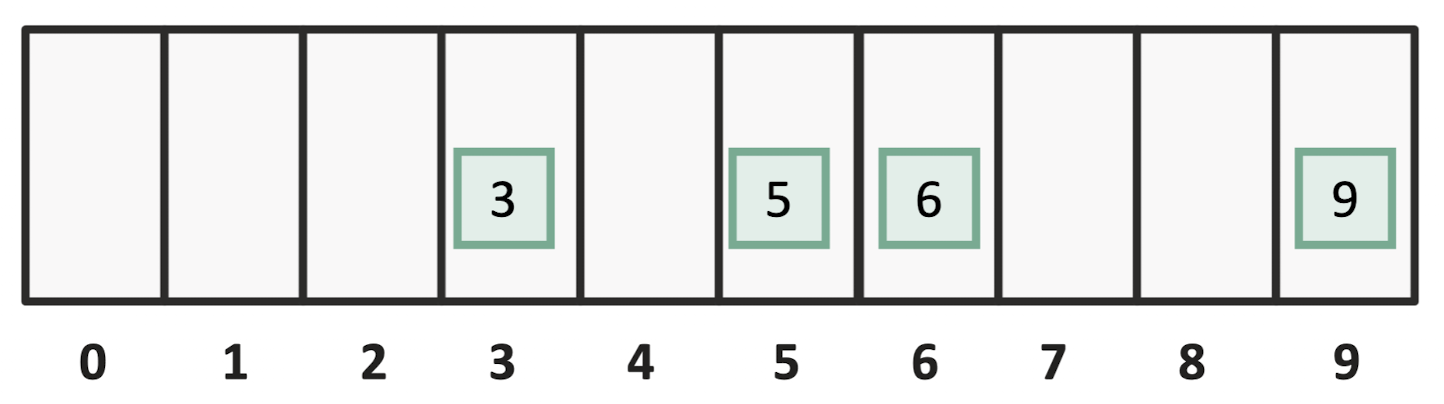
이렇게 한 칸에 하나씩 본인의 자리에 넣는 것을 Direct Addressing이라고 한다.

정말 빠르게 처리할 수 있다는 장점이 있지만, 무지막지한 공간이 필요하다는 단점이 있다.

이 세상에 존재하는 모든 수를 담고 있는 집합을 $U$ 라고 하고 개수를 $M$이라고 했을 때 M개의 공간이 필요하다는 것이다.

Digit

저 말도 안되는 범위를 해결하기 위해 1의 자릿수를 기준으로 구분해서 넣어볼려한다.

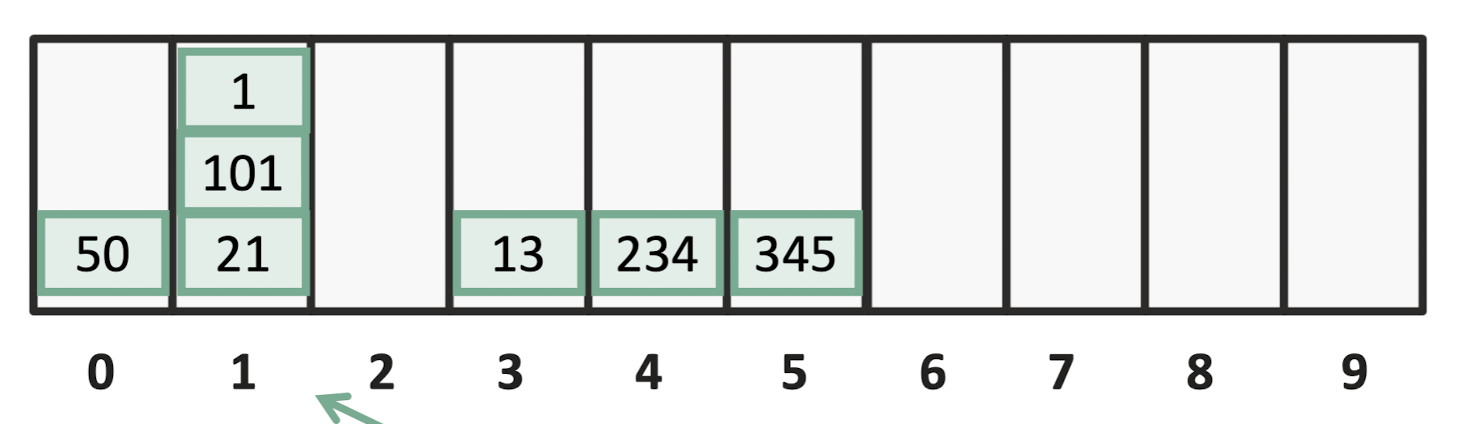
오 나름 합당해보인다.

근데 또 문제가 생긴다.

어떤 정신 나간 놈이 친절히 1의 자리수가 2인 수만 잔뜩 줬다.

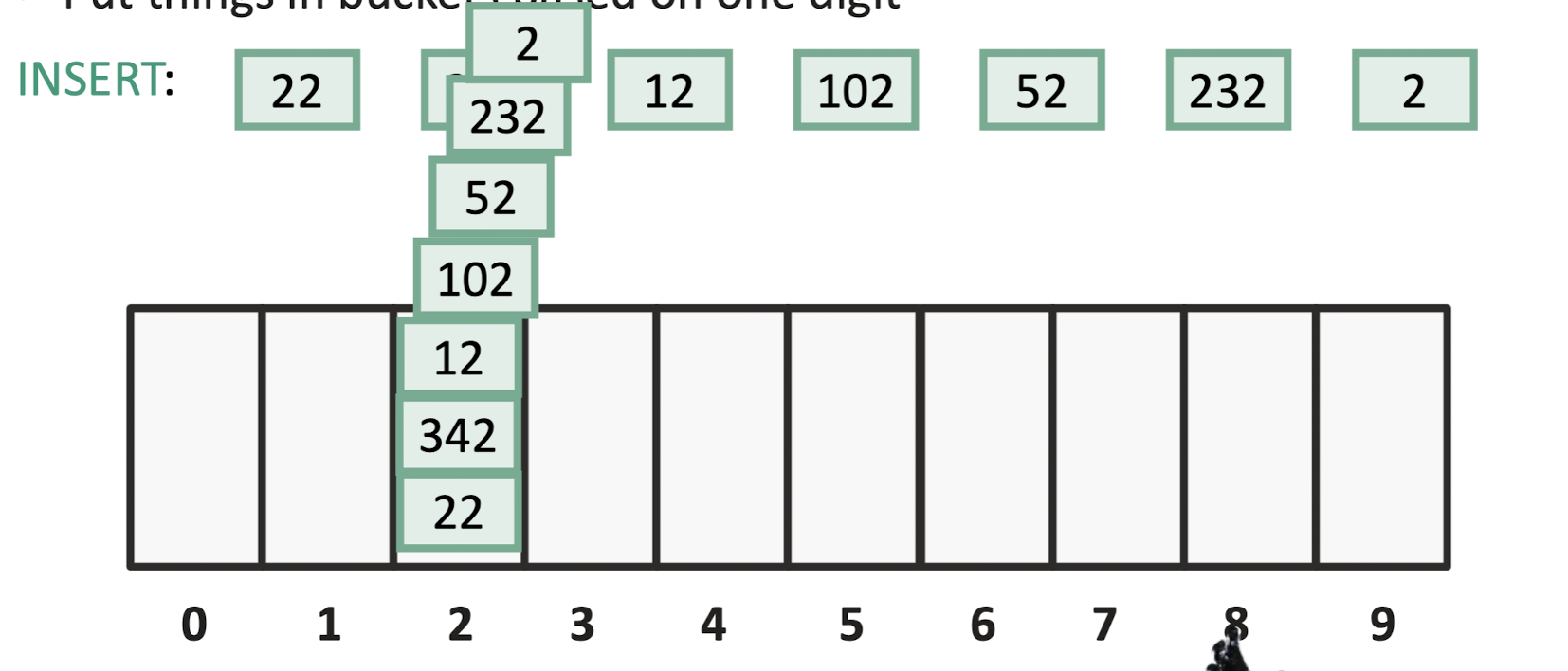
하...

이 방법도 기각이다.

Hash Function

그래서 우리는 n개의 bucket을 가진 hash table을 만들고, x에 대해 특정한 bucket의 위치를 반환하는 hash function인 h(x)를 만들 것이다.

예를 들면 $h(x) = least \ significant \ digit \ of \ x$ 라고 할 수 있다.

하지만 이렇게 고정된 hash function은 누군가의 방해를 막을 수 없다.

우리는 잘 퍼지고, 충돌도 안 일어나는 이상적인 hash table을 민들고 싶지만, $M$은 너무나도 큰 값이고, 우리는 그 중 $n$개를 다루고, 그 $n$개를 예상 할 수 없기 때문에 사실상 불가능하다.

Randomness

자 팔협지 비기 "무작위"

$n$개의 수에 대해서 무작위로 bucket 위치를 정해주는 것이다.

비유를 하자면 전교생에게 아무런 규칙 없이 1인당 1개의 별명을 붙여주는거다.

또한 이 무작위는 1명 1명에 대해 모두 독립 시행이다.

이런 방법이라면 그 누구도 방해할 수 없다.

이 숫자가 어디에 들어갈지는 나도 모르는데 이걸 어떻게 알건데.

Prove

우리는 하나의 bucket에 숫자가 2개 이하로 들어가는 경우를 이상적인 경우로 정의하고, 이게 가능하다는 것을 증명할 것이다

어떤 수가 bucket에 들어갈 확률은 $1/n$ 이다.

그리고 그 bucket 안에 이미 수가 하나 있다고 가정하면, 남은 모든 수들에 대해서 그 안에 들어갈 수의 기대값은 $n-1/n$이다.

그 이미 들어가 있는 수를 포함하면 총 $1+ (n-1)/n$이 기대값이 된다.

$(n-1)/n \leq 1$이므로 $1+ (n-1)/n \leq 2$ 가 성립한다!

But...

하지만 이것에도 문제가 있다.

우리는 이 수들의 hash code, 즉 어디에 들어있는지 다 기억해야한다.

완전 무작위로 돌렸기 때문에 일일이 다 기억해야한다.

$n$개의 수를 표현하기 위해서 $log(n)$ bit가 필요하기 때문에, 총 $Mlog(n)$bit 의 저장공간이 있어야한다.

$M$의 크기가 크지 않다면 상관 없겠지만, 매우 크다면 아무래도 문제가 될 것이다.

Hash Family

그래서 우리는 Hash Family라는 것을 이용할 것이다.

Hash Family($H$)는 hash function들의 집합으로, hash function을 무작위로 선택하여 적용할 것이다.

hash function이 2개만 있다고 가정하면 $log_22 = 1$bit만 있으면 된다.

어차피 $U$에 있는 모든 수에 대해서 적용할 수 있다는 것이 hash function의 특징 이므로 $M \times log_22$를 할 필요는 없다.

무작위는 $H$ 안에서만 적용하면 된다.

하지만 이렇게 고정된 function이거나 개수가 적다면 충분히 방해를 할 수 있다.

Universal Hash Families

위의 모든 방법을 다 해결할 수 있는 마법같은 방법이 있다.

바로 Universal Hash Families이다.

기본적인 전략은 어떤 $h(x)$를 선택해도 $h(u_i) = h(u_j)$인 확률이 $1 \over n$ 이하로 만드는 것이다.

Example

정말 많은 Universal Hash Families가 있겠지만, 그 중에서 가장 대표적인 예시를 하나 들어보겠다.

일단 아래와 같이 함수를 정의한다.

• $p \geq M$ ($p$는 소수)
• $f_{a,b}(x) = (ax+b) \ mod \ p$
• $h_{a,b}(x) = f_{a,b}(x) \ mod \ n$
• $H = \{h_{a,b}(x) : a \in \{ 1, ... p-1\}, b \in \{ 0, ... p-1\}\}$

이렇게 정의된 함수에 대해서 설명을 덧붙이자면,
소수인 $p$를 정의하여 $mod \ p$를 시행 했을 때 겹치는 수 없이 hash code를 지정할 수 있고(= 별명을 겹치지 않지만 규칙적으로 붙임), 그 결과를 $mod \ n$을 통해 겹치는 bucket 없이 고르게 분배할 수 있다.

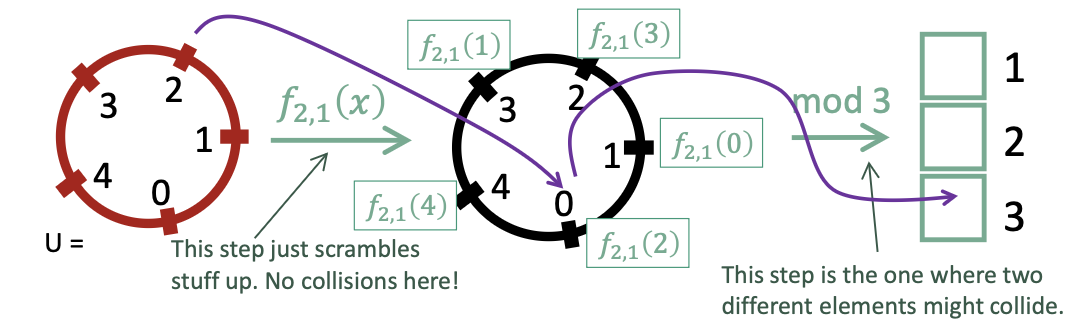
이런 경우, $H$에 대해서만 randmize를 실행하므로, a와 b가 어떤 수 였는지만 기억하면 된다.

a와 b 모두 대충 p개의 경우가 있고, p개를 나타내기 위해서는 $log_2(p)$bit만 있으면 된다.

2개에 대해서만 고려하면 되므로 총 $2 \times log_2(p)$bit라고 볼 수 있다.

$p$는 $M$과 아주 가까운 수일 것이므로, 일반화하여 $O(log(M))$bit 정도 사용한다고 볼 수 있겠다!

direct adrressing에 비해 훨씬 안전하며, uniform radomize에 비해 훨씬 적은 bit를 사용한다.

Conclusion

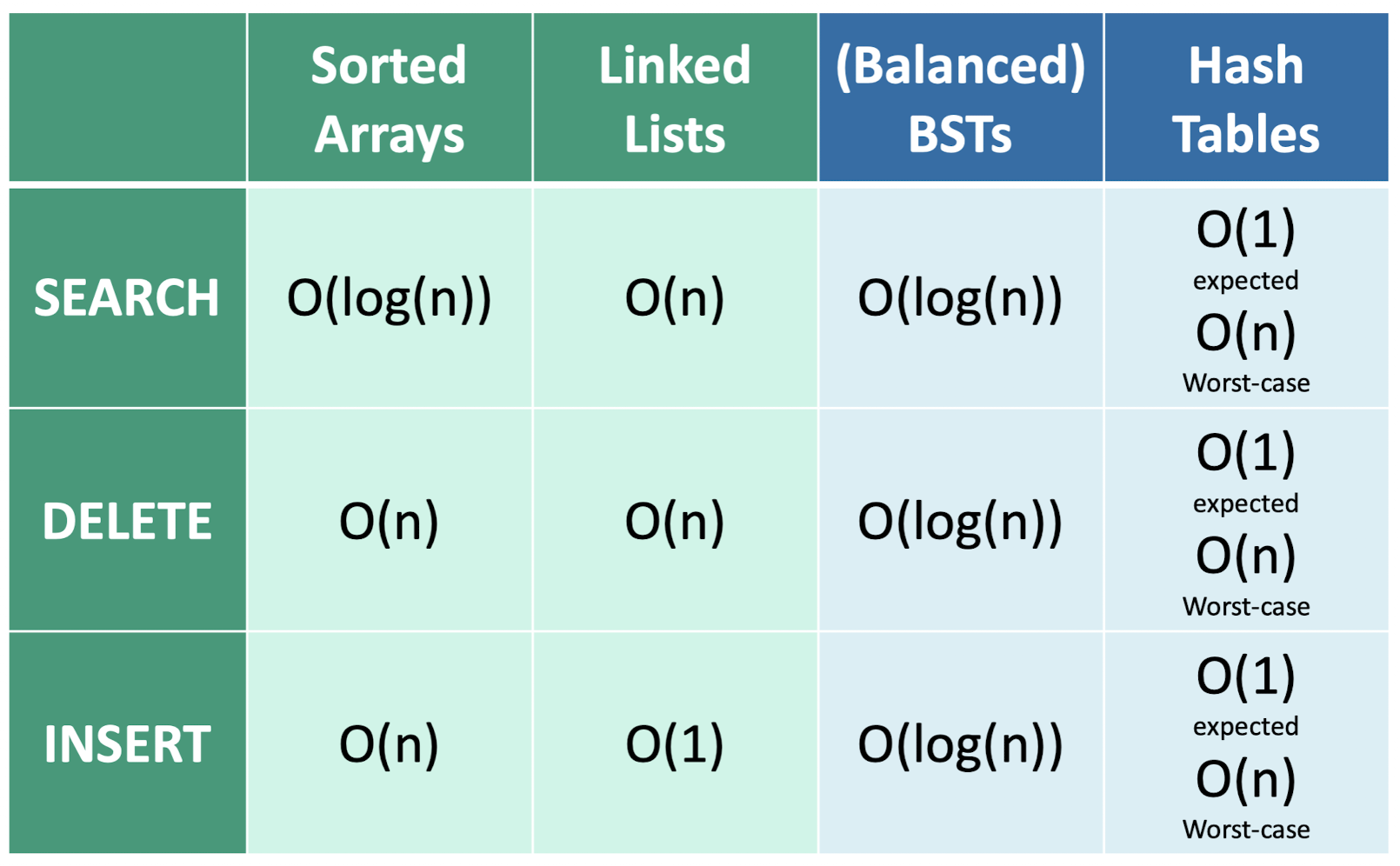
이 표를 마지막으로 잘 기억하도록 하자!!