Merge Sort

바로 직전 글에서 Insertion Sort를 다뤘었다.

하지만 Insertion Sort의 worst case의 시간 복잡도는 $O(n^2)$이기 때문에 마냥 빠르다고 할 수는 없다.

그래서 시간을 개선하기 위해 또 다른 방법을 고안해야한다.

Divide and Conquer

Divide and Conquer (분할-정복법), 줄여서 DnC라고도 부른다.

말만 들으면 뭔가 싶겠지만 사실 이게 가장 직관적인 표현이다.

커다란 하나의 Task를 작은 tasks로 나누어서 문제를 해결하는 것이다.

이 방법이 뭐가 좋냐고 묻는다면 3가지를 알려주겠다.

1. 일 하나의 난이도가 낮아진다.
   • 10개 줄 세우기 vs 2개 줄 세우기를 고르라면 당연히 후자다.
2. 병렬 처리를 할 수 있다.
   • 일을 여러 개로 나누면 여러 곳에서 동시에 수행할 수 있다.
3. 메모리 대신 캐시를 사용할 수 있다.
   • 캐시를 사용하면 속도가 빨라진다는 것은 컴구를 배웠다면 알 것이다.

Logic

이제 Merge Sort의 기본적인 아이디어를 알아보자.

Dnc를 사용한다 했으니 리스트를 자르는 것은 당연하다.

1. 단 절반을 자른다.
2. 제 붙이며 정렬한다.

장난치는 거 아니냐고? 진심이다.

슈도 코드도 그렇게 말하고 있지 않은가.

물론! 이걸 재귀적으로 진행해야한다.

그럼 리스트들은 1개로 쪼개지게 될 것이고 그걸 정렬하면서 붙여나가면 된다.

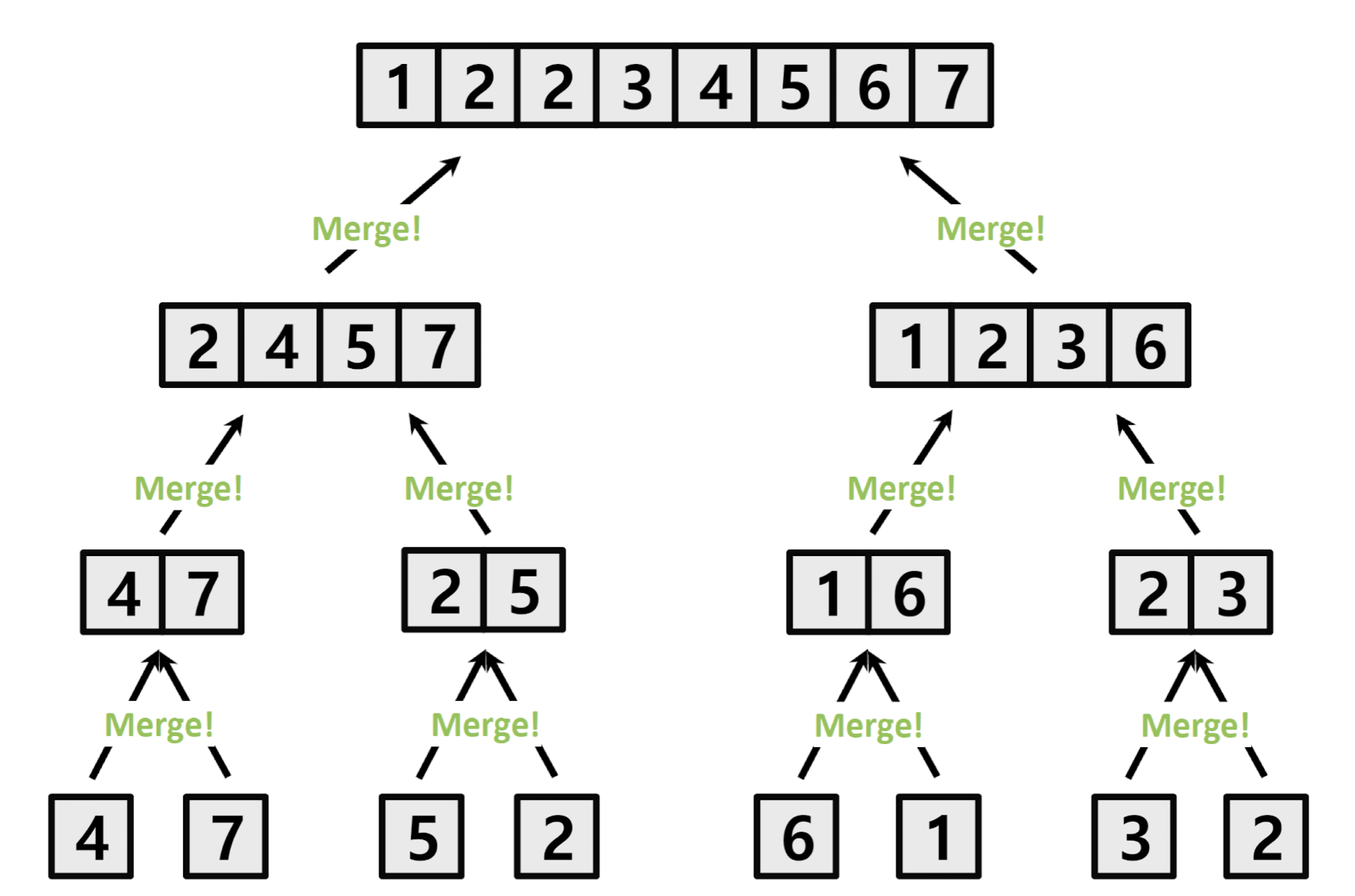
이러면 된다는 거다.

아 그럼 자르는 건 알겠는데 정렬하면서 붙이는 건 어떻게 하냐고?

1. 정렬된 두 개의 sub list(Left, Right)를 준비한다.
2. 두 리스트의 가장 앞에 있는 것 중 더 작은 것을 선택한다.
3. 원본 리스트에 넣는다.
4. 선택된 리스트의 inedex를 1 늘린다.
5. 모든 sub list를 다 쓸 때까지 반복

슈도 코드가 있긴 한데 이게 더 가독성이 떨어지는 거 같다.

Prove

암튼 또 썩을 증명 한 번 하자.

알고리즘이 재귀를 하고 있긴 하지만 실질적은 로직은 Merge 부분에서 수행되므로 여기가 증명되어야한다.

그럼 Loop Invariants를 통한 증명을 해야겠지?

여기서는 변하지 않는 것이 2개있다.

1. k번째 반복문에서 $A[p:k-1]$은 항상 정렬되어있다. 즉 L, R 중 $k-p$번째로 작은 수가 포함되어있다.
2. $i$, $j$가 각각 가리키는 값은 L과 R의 최솟값이다.

이를 증명하여보자.

1. 초기 조건

   • $k=p$ 이므로 $A[p:k-1]$은 empty list
   • $k-p=0$ 이므로 L, R 중 가장 작은 수가 포함됨.
   • $i=j=1$ 이므로 L, R 모두 본인의 가장 작은 수를 가르킴

2. 유지 조건

   • 하나의 수가 A에 추가 되었을 때, 그 수는 $k-p+1$번째로 작은 수.
   • 또한 $i$ 또는 $j$가 1 증가했을 것이므로 여전히 가장 작은 수를 가르킴.

3. 종료 조건

   • $k=r+1$인 경우 종료.
   • 이 때 $k-p=r-p+1$번째로 작은 수를 포함.

Time Complexity

Merge Sort처럼 재귀적으로 실행되는 알고리즘의 경우, 재귀 방정식을 통해 설명할 수 있다.

3단계로 나누어보자.

1. Divide: 두 개로 나누는 건 나누기 연산 한 번에 종료된다 -> $\Theta(1)$

2. Conquer: 나눠진 두 list를 해결하는 시간 -> $T(n/2) + T(n/2)$

3. Combine: 두 list를 합치는 시간 -> (길어봐야) $\Theta(n)$

원소가 1개일 때는 1번이면 되니 $T(1)=1$이라고 정의하자.

그리고 simplification을 거치면 아래와 같은 식이 나오게 된다.

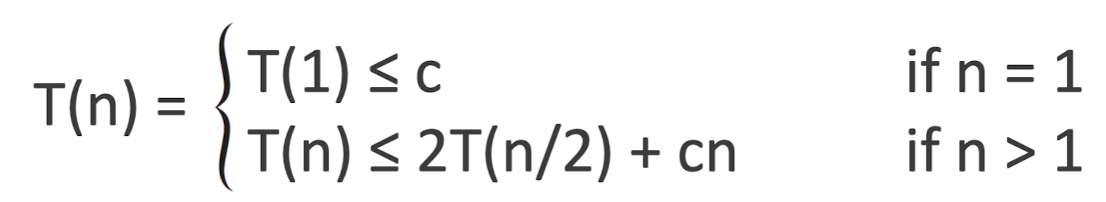
일단 결론만 말하자면 $\Theta(nlog_2n)$ 시간이 걸린다.

이걸 구하는 것에는 총 3가지 방법이 있는데, 그건 다음 글에서 다루도록 하겠다.