Methods

전 글에서 다뤘던 Merge Sort와 같이 재귀를 사용하는 알고리즘의 Run Time을 분석하는 방법에는 3가지가 있다.

재귀는 하나의 로직을 파고 파고 들어가는 형식이기 때문에 점화식만 보고 Run Time을 알아내는 것에는 분명 무리가 있다.

Recursion Tree Method

3가지 방법 중 첫번째는 Recursion Tree이다.

말 그대로 구조를 Tree로 나타내서 생각하면 된다.

Merge Sort의 Recursion Tree를 함께 살펴보자.

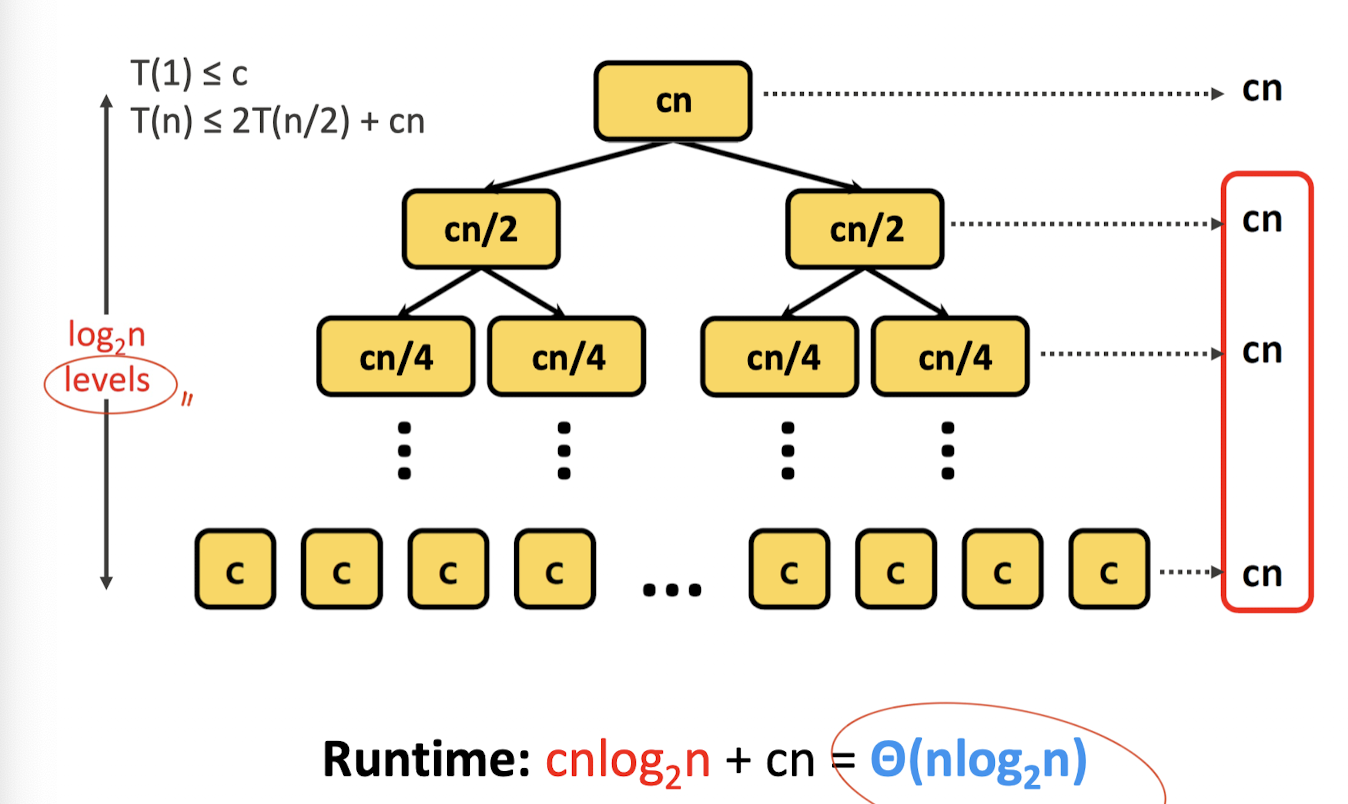
Merge Sort의 점화식을 리마인드 해보자.

$n=1$ 일 때, $T(n)=1$
$n \geq 1$ 일 때, $T(n)=2T(n/2)+ \Theta(n)$
이다.

트리의 root는 $n=1$ 인 경우를 나타내고 있고, 그 아래는 $n$이 증가할 때 마다의 진행을 나타낸다.

DnC의 경우 sub task의 size가 1이 될 때 까지 진행하므로, 결국 하나의 실행 시간은 $c$가 될 것이다.

Merge Sort처럼 균등하게 나눠지는 경우, 하나의 level에서 같은 시간만큼 소요되며, 그 말은 level의 수만큼 $cn$의 시간이 걸리므로 총 시간은 $cn+cnlog_2n$이 된다.

정량적인 표기를 하면 $\Theta(nlog_2n)$이 될 것이다.

Recursion Tree Method 같은 경우 눈에 보이기 때문에 그렇게 어렵지 않다.

하지만 일일이 그려야한다라는 불편함이 있을 수 있겠다.

Master Method

이름에서 알 수 있듯이, 이 친구는 좀 전지전능한 친구이다.

호텔의 Master Key를 생각해도 될 듯하다.

하지만 Master Key라도 언제 어디서나 모든 곳에서 사용되는 것은 아니다.

그 호텔 내부에서만 Master Key인 것이지, 그거 들고 우리 집 문 딸려고 하면 안 된다는거다.

그래서 그 호텔이 뭔데? 라고 물어본다면 아래의 호텔을 말해주겠다.

$T(n)=a \times T(n/b) + O(n^d)$

우리의 전지전능하신 Master Method님은 이렇게 생겨 먹은 식에 대해서만 쓸 수 있다는 것이다.

그리고 그냥 막 써도 되는 것도 아니다.

3가지 경우가 나뉘는데, 그건 사진으로 대체하겠다.

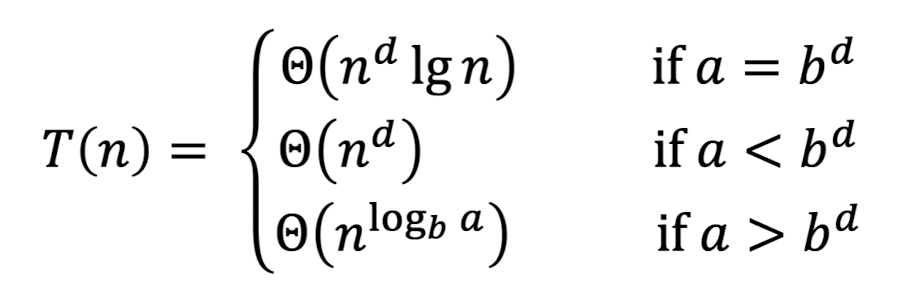
이걸 한 번 Merge Sort에 적용해보자.

$a=2, b=2, d=1$ 이므로, $a=b^d$ 이다.

그럼 $T(n)= \Theta(nlog_2n)$ 이겠지?

와!

Recursion Tree로는 그림 한 세월 그리고 level별로 시간 계산해주고 정량적 표기까지 했을 때의 결과를 숫자 대입 몇 번에 끝내버렸다.

그냥 이렇게 쓸 수 있다! 만 알면 참 좋겠지만 우리는 이게 왜 이렇게 되는지 궁금해야한다.

Prove

대신 뚝딱 이해할 수 있게 사진 하나를 첨부해주겠다.

앞서 배웠던 Recusion Tree를 이용한 증명을 할 것이다.

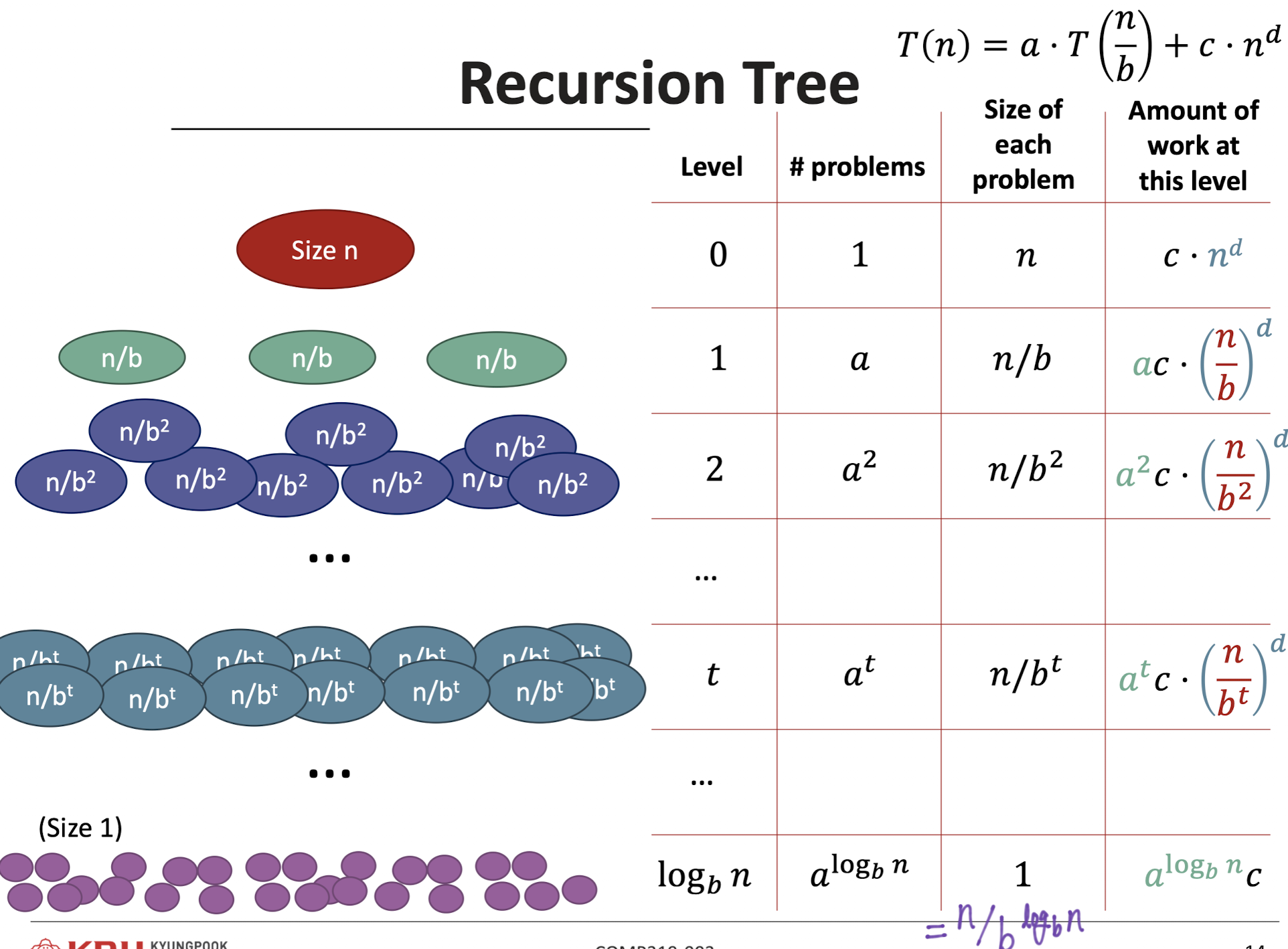
우리는 이 중에서 마지막 Column에 집중할 것이다.

level이 t일 때의 run time은 $a^t \times c \times (n/b^t)^d$이다.

이걸 t로 묶어서 정리하면 $n^d \times c \times (a/b^d)^t$ 가 된다.

그럼 sub tasks의 run time의 합은 아래와 같아진다.

$T(n) = c \times n^d \times \sum_{t=0}^{log_bn} (a/b^d)^t$

그럼 여기서 처음 Master Method를 다시 한 번 보자.

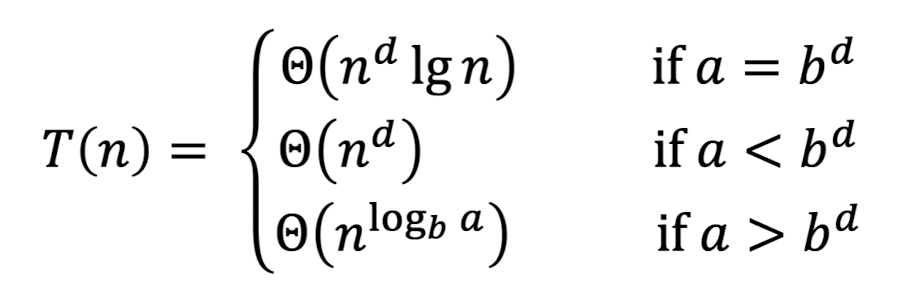
뭔가 느껴진다면 당신은 수학에 감각이 있는 듯하다.

그렇다. $a/b^d$의 범위에 따라 수식이 결정되는 것이다.

각각의 Case에 대한 수학적 증명은 아래와 같으니 참고하도록 하자.

수학적 증명은 잠깐 접어두고 직관적으로 와 닿는 설명을 곁들여주자.

Case 1

Case 1의 경우는 sub task가 생기는 양과 한 번에 처리해야 할 일의 크기가 줄어드는 속도가 같은 경우이다.

모든 level이 균등하게 실행 시간에 영향을 준다는 것이다.

Case 2

Case 2의 경우는 sub task가 생기는 양 보다 일의 크기가 줄어드는 속도가 더 빠른 경우이다.

sub task는 level 당 2개씩 생기는데 하나의 task가 n/4 만큼의 일을 수행한다면?

밑에 애들이 뭘 하든 별 관심이 없어진다.

그냥 맨 위의 일만 끝나면 밑에 일은 다 끝나있을것이다.

Case 3

Case 3의 경우는 sub task가 생기는 양이 일의 크기가 줄어드는 속도보다 더 빠른 경우이다.

sub task가 4개씩 생기는데 하나의 task가 n/2만큼 밖에 일을 하지 못한다면 맨 아래에서는 하루 종일 일을 해야한다는 것이다.

맨 아래에서 일이 끝났다면 아마 그 위는 이미 다 끝내고 놀고 있겠지.

My case

어떻게 느꼈는 지는 모르겠지만 이 얘기를 한 번 들은 이후로는 외운다기보다는 이해의 영역에 좀 더 가까워진 것 같았다.

식이 기억이 안 난다면 이걸 한 번 떠올리도록 하자.

Substitution Method

가장 귀찮다고 느껴질 방법 중 하나이다.

하지만 수학적 증명에 딱히 거부감을 느끼지 않는다면 가장 정확한 방법일지도 모른다.

수식은 거짓말을 하지 않는다는 것은 정말 자명한 사실이니 말이다.

설명을 들을 때는 정답을 예상하고 끼워 맞추기라는 느낌으로 배웠지만 딱히 그런 것 같지는 않다.

그냥 논리적 사고가 아닌가...

암튼 이건 설명보다 보는 것이 훨씬 빠르다.

이번에도 Merge Sort의 예를 들어보자.

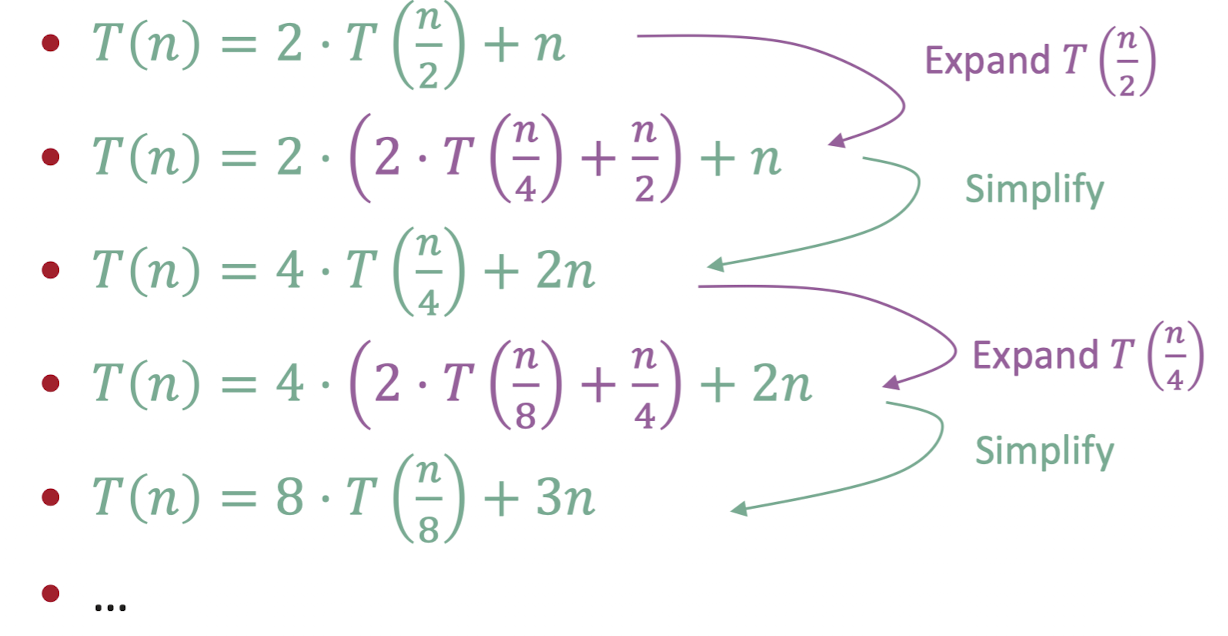
어쩌면 이게 가장 재귀를 잘 나타내는 것 일지도 모른다.

아무튼 결국 이런 패턴을 발견할 수 있다.

$T(n)=2^t \times T(n/2^t) + t \times n$

또한 우리는 결국 sub task의 크기가 1이 될 때까지 재귀하는 것이 목적이므로, $n/2^t = 1$ 이라는 것을 기반으로 위의 식에 대입할 것이다.

결국 $T(n) = n(logn+1)$이라는 식이 나오게 된다.

$n=1$ 일 때 두 식 모두 $T(1)=1$ 이므로 $k$ 일 때도 성립하는지 보자.

딱히 어려운 부분은 없다.

원본에 k 대입 -> 식 변환 -> 동일한 지 확인

결국 $\Theta (nlogn)$ 임을 증명하였다.

조금 공식화를 해보자면,
패턴 찾기 -> 단순화 -> 모든 케이스에 대해 성립하는 지 확인
의 과정을 거치면 된다.

Conclusion

이렇게 3개의 방법으로 Merge Sort가 $\Theta (nlogn)$ 시간을 가진다는 것을 알게 되었다.

확실히 Insertion Sort 보다는 빠른 모습이다.