[Java] LCS - Longest Common Substring / Longest Common Subsequence (자바 | Java)

[Java] LCS - Longest Common Substring / Longest Common Subsequence

---

LCS

LCS는 통상 Longest Common Subsequence의 준말로, 최장 공통 부분수열을 의미한다.
그러나 이와 비슷하게 최장 공통 문자열인 Longest Common Substring도 존재한다.

이 둘의 차이점은 아래와 같다.

• Substring : 전체 문자열에서 연속된 부분 문자열
• Subsequence : 전체 문자열에서 공통 되면서 가장 긴 부분 문자열

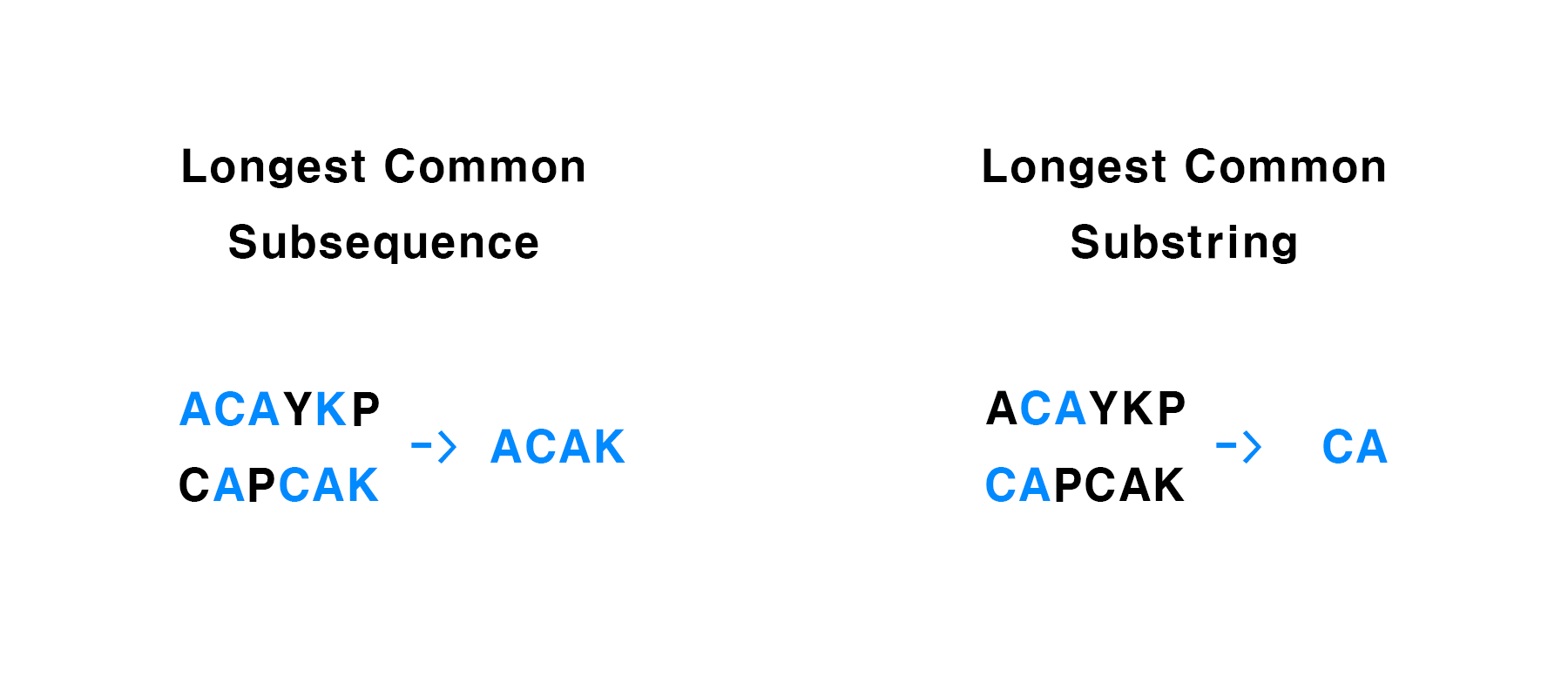
이제 위 예시를 바탕으로 2차원 배열을 이용해 Substring과 Subsequence 를 구현 해보겠다.

Longest Common Substring

최장 공통 문자열은 최장 공통 부분 수열을 구하는데 사용 되기에 간단히 알아보겠다.

점화식

// str1 = ACAYKP
// str2 = CAPCAK
for (int i = 1; i <= str2.length(); i++) {
	char c = str2.charAt(i - 1);
	for (int j = 1; j <= str1.length(); j++) {
    	if (c == str1.charAt(j - 1)) {
        	dp[i][j] = dp[i - 1][j - 1] + 1;
        } else {
        	dp[i][j] = 0;
        }
    }
}

코드로 작성을 해봤다. LCS는 다이나믹 프로그래밍으로 구현한다.
2차원 배열을 이용해 str1, str2를 행, 열에 배치하고 검사를 한다.

1. str1, str2를 한 글자씩 비교한다.
2. 두 문자가 같다면 dp[i - 1][j - 1] + 1 을 한다.
3. 두 문자가 다르다면 dp[i][j] = 0을 한다.
4. 끝까지 반복한다.

최장 공통 문자열이기 때문에 연속된다면 2번, 연속되지 않는다면 3번과 같은 식이 나온다.

Longest Common Subsequence

점화식

// str1 = ACAYKP
// str2 = CAPCAK
for (int i = 1; i <= str2.length(); i++) {
	char c = str2.charAt(i - 1);
	for (int j = 1; j <= str1.length(); j++) {
    	if (c == str1.charAt(j - 1)) {
        	dp[i][j] = dp[i - 1][j - 1] + 1;
        } else {
        	dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
        }
    }
}

최장 공통 문자열과 비슷하지만 else문에서 차이가 있다.

1. str1, str2를 한 글자씩 비교한다.
2. 두 문자가 같다면 dp[i - 1][j - 1] + 1을 한다.
3. 두 문자가 다르다면 dp[i - 1][j]와 dp[i][j - 1]중 큰 값을 선택한다.
4. 끝까지 반복한다.

구현

1. 2차원 배열을 아래와 같이 생성 후 비교를 시작한다.
   

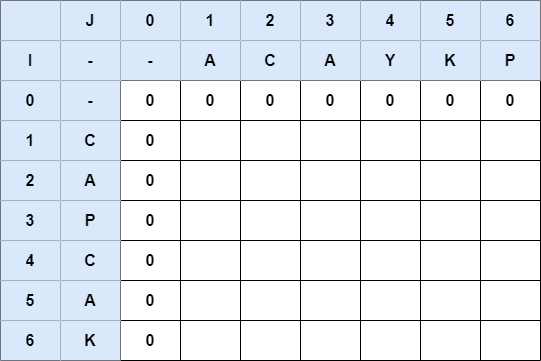
2. 두 문자가 같으면 dp[i - 1][j - 1] + 1을 한다.
   

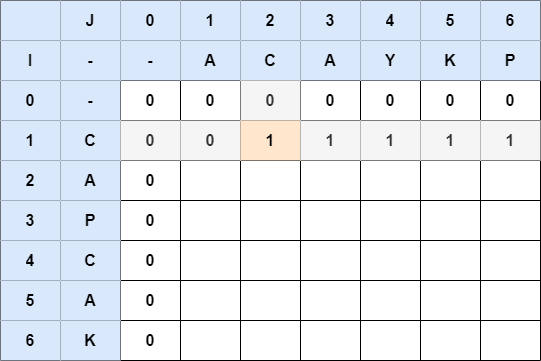
그런데 (1, 3), ..., (1, 6) 이 모두 1로 되어있다. 그 이유는 위 점화식 3번에 해당한다.

• AC 와 C를 비교하여 1이 되었고, 그 다음 ACA와 C를 비교할 때 이전의 최대 공통 부분 수열은 A로 그 길이는 1이 된다.
  즉, 이전의 값을 확인하여 사용 하므로 다이나믹 프로그래밍으로 생각할 수 있다.

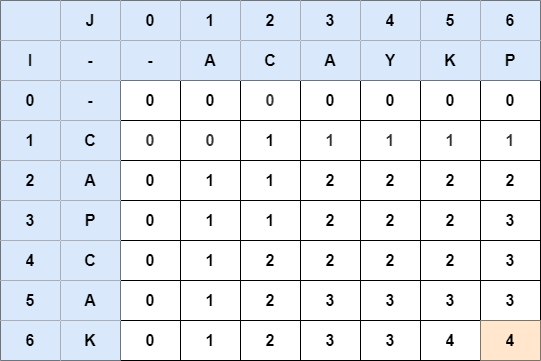
최장 공통 부분 수열이 ACAK가 되었을때는 다음과 같이 배열이 채워진다.

3. 최장 공통 부분 수열의 길이인 dp[6][6]은 4가 된다.