[Java] Union-Find 유니온-파인드 구현 (자바 | Java)

[Java] Union-Find 유니온-파인드 구현

---

Union-Find?

유니온-파인드는 그래프 알고리즘 중 하나이다. '합집합 찾기' 라는 의미를 가지고 있다.
서로소 집합(Disjoint-Set) 알고리즘이라고도 부른다.
여러 개의 노드가 존재할 때 두 개의 노드를 선택해서, 현재 이 두 노드가 서로 같은 그래프(집합)에 속해있는지 확인하는 알고리즘이다. 따라서, 아래 두 가지 연산이 존재한다.

1. Union
   노드 x가 포함된 집함과 노드 y가 포함된 집합을 합치는 연산

2. Find
   노드 x가 어느 집합에 포함되어 있는지 찾는 연산
   위 연산을 아래 로직과 함께 같이 이해 해보도록 하겠다.

로직

위와 같이 여러 개의 노드가 존재하고, 이들은 모두 연결되지 않고 각자 자기 자신만을 집합의 원소로 가지고 있을때 다음과 같이 표현할 수 있다. 바로 모든 값이 자기 자신을 가리키는 것이다.
이는 배열로 구현이 가능하다.

1	2	3	4	5	6
1	2	3	4	5	6

int[] parent = new int[7];
for (int i = 1; i <= 7; i++) {
	parent[i] = i;
}

Union(1, 2), Union(3, 4) 를 하여 노드를 연결하면 아래와 같다.

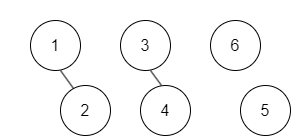
1	2	3	4	5	6
1	1	3	3	5	6

표(배열)은 위와 같이 표현 된다. 일반적으로 더 작은 값 쪽으로 Union 연산을 한다.

그렇다면 1, 2, 3이 Union 된다면 어떻게 될까?

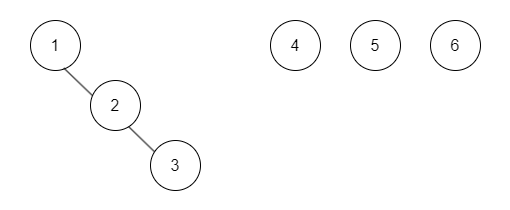
1	2	3	4	5	6
1	1	2	4	5	6

그러나 여기서 '1과 3이 연결 되어있는가?' 하는 의문이 생긴다. 2와 3은 부모가 각각 1과 2로 다르기 때문에 '부모 노드' 만 보고는 한 번에 파악 할 수 없다. 따라서 이때 재귀 함수 가 사용 된다.

3의 부모인 2를 찾고, 2의 부모인 1을 찾으면 '결과적으로 3의 부모는 1이다' 라는걸 파악 할 수 있다.
이러한 과정은 재귀적으로 구현 할 수 있으며 find 연산을 통해 구현 할 수 있다.

결과는 다음과 같다.

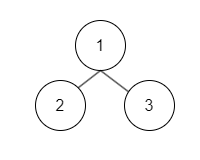
1	2	3	4	5	6
1	1	1	4	5	6

구현

public class Main {
  public static void main(String[] args) {
          for(int i = 1; i <= 6; i++) {
              parent[i] = i;
          }
          union(1, 2);
          union(2, 3);
      }
	
    public static int find(int x) {
        if(parent[x] == x)
            return x;	
        else 
        // 재귀를 통해 부모노드를 계속해서 찾아감
            return parent[x] = find(parent[x]);
	}
	
    public static void union(int x, int y) {
        x = find(x);
        y = find(y);
        // 가르키는 부모노드가 다를때
        if(x != y) {
            parent[y] = x;
        }
    }
    
    //같은 부모 노드인지
    public static boolean isSame(int x, int y) {
        if(find(x) == find(y))
            return true;
        else
            return false;
    }
}

이 알고리즘은 MST(최소신장트리)를 구현 할 때 쓰이는 크루스칼 알고리즘에 활용 되기에
알아두면 좋을것 같다.

---

출처

나동빈님 블로그