Intro
오늘은 부스트캠프 멘토링 시간에 가졌던 주제에 대해 다뤄보려고 한다. 항상 weight initialization에 대해 많은 궁금증이 있었지만 막연하게 해당 모델에서 많이 사용되는 initialization을 쓴 것 같다. 오늘은 조금더 심도 있게 알아보도록 하자
1. Weight Initialization 종류
딥러닝 학습에 있어 가중치 초기화는 매우 중요한 역할을 한다. 가중치를 잘못 설정할 경우 기울기 소실 문제나 표현력에 있어 한계를 갖는 등 여러 문제를 야기하게 된다. 또한 딥러닝의 학습의 문제가 non-convex이기 때문에 초기 값을 잘못 설정할 경우 local minimum에 수렴할 가능성이 커지게 된다.
우선 가중치 초기화 종류에 대해서 알아보자
1-1) LeCun Initialization
초기 CNN인 lenet으로 유명한 Yann Lecun 교수님의 페이퍼에서 제안된 기법이다. 기본적으로 uniform distribution 혹은 normal distribution에서 추출한 랜덤 값으로 웨이트를 초기화 시키되, 이 확률 분포를 fan-in 값으로 조절하자는 아이디어이다. 수식으로 표현하면 아래와 같다.
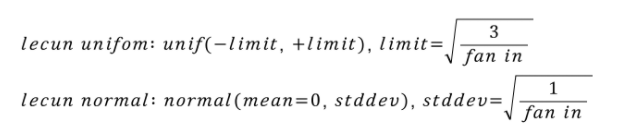
핵심 아이디어는 신경망에 들어오는 input의 크기가 커질수록 초기화 값의 분산을 작게 만들자는 것이다. 그 결과로 0에 가까운 더 작은 값들이 추출되게 된다.
간단하게 numpy로 다음과 같이 구현해볼 수 있다.
import numpy as np
node_num = 100 # 각 은닉층의 노드(뉴런) 수
w = np.random.randn(node_num, node_num) * 0.011-2) Xavier Glorot Initialzation
다음으로는 현재에도 많이 사용되는 초기화 기법인 Xavier Glorot Initialization이다. 수식으로 살펴보면 아래와 같다.
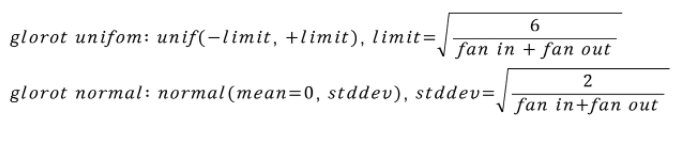
핵심 아이디어는 fan in과 fan out을 모두 고려하여 확률 분포를 조정해준다는 것이다.
마찬가지로 간단하게 numpy로 다음과 같이 구현해볼 수 있다.
w = np.random.randn(node_num, node_num) * np.sqrt(1.0/node_num)1-3) He Initialization
Glorot 기법의 한계를 극복하기 위해 Kaming He가 2010년 제안한 기법이다. Resnet을 학습시킬 때 이 기법을 사용하여 실제로 깊은 CNN 신경망을 학습시킬 때 잘 작동함을 보여주었다. 수식으로 표현하면 아래와 같다.
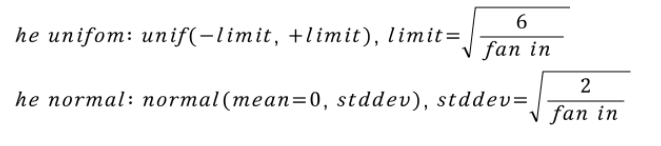
수식을 살펴보면 glorot 기법에서 다시 fan out을 제거한 모습을 보인다.
2. activation function과의 관계
activation function은 대표적으로 3가지 종류가 있다.
Sigmoid 함수
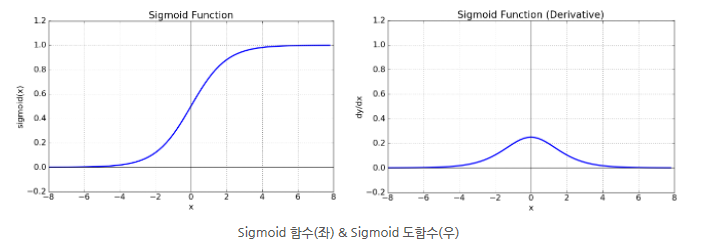
def sigmoid(x):
return 1 / (1 + np.exp(-x))Tanh 함수
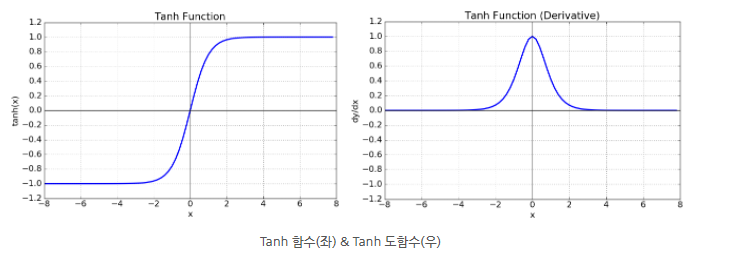
def tanh(x):
return np.tanh(x)ReLU 함수
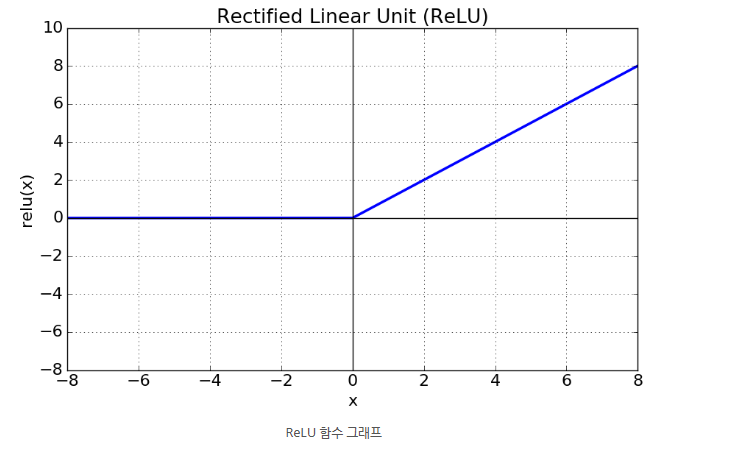
def ReLU(x):
return np.maximum(0, x)위에서 언급된 가중치 초기화와 activation 함수를 조합해보자
위의 깃헙 코드를 참고하여 테스트 해보았다.
우선 sigmoid 함수의 경우 출력 값이 0과 1에 가까워 질수록 gradient 값이 0에 가까워 짐을 알 수 있다.
일반적인 가우스 분포의 가중치 초기화를 사용하게되면 다음과 같은 히스토그램을 보여준다.
여기서 히스토그램의 x축은 활성화 함수의 출력 값이다.
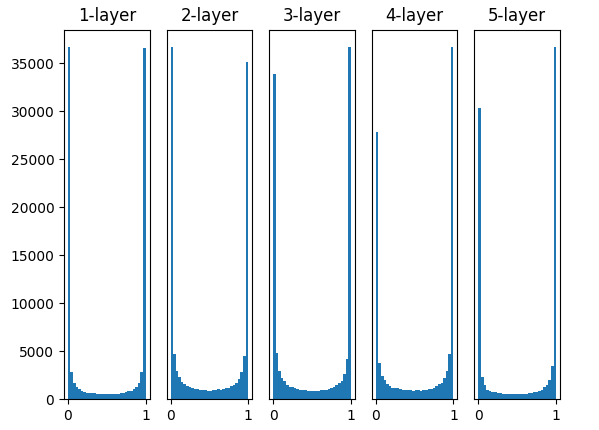
0과 1의 값이 상당히 많으므로 back propagation이 시행될 때 gradient vanishing 문제가 일어날 수 있음을 짐작해 볼 수 있다.
Lecun 가중치 초기화를 사용하면 어떨까?
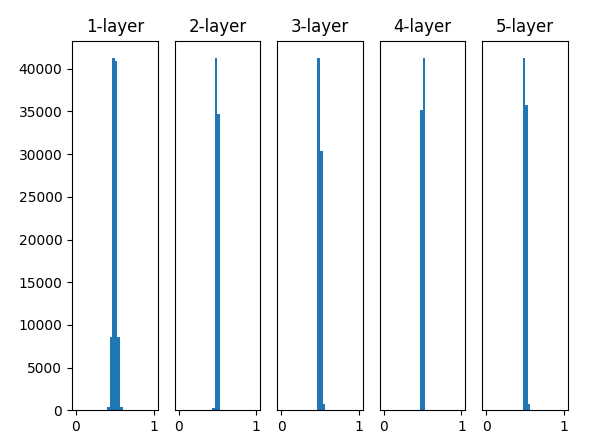
일단 0과 1의 값이 없기 때문에 정상적으로 보일 수 있다. 하지만 우리가 활성화 함수를 사용하는 이유를 생각해 보는것이 좋다. 활성화 함수는 비선형 관계를 표현하기 위해 사용된다. 하지만 출력값이 0.5에 근사하게되면 sigmoid 함수는 선형적인 관계만을 표현할 수 없게 된다는 한계를 갖게 된다. 즉 이러한 문제 때문에 sigmoid 함수를 잘 사용하지 않는다고 할 수 있다.
현재 가장 많이 사용되는 활성화 함수는 ReLU 활성화 함수이다. 그렇다면 ReLU 활성화 함수는 어떤 가중치 초기화와 잘 맞는다고 할 수 있을까?
다음은 LeCun 초기화와 사용한 결과이다.
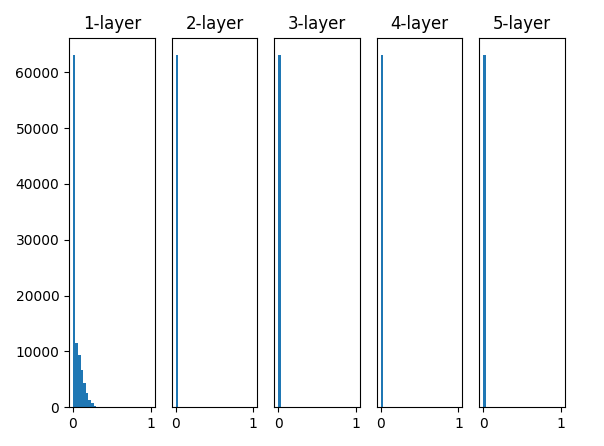
결과를 보면 layer가 깊어질 수록 출력 값이 0으로만 표현되게 된다. 직관적으로 문제가 있음을 알 수 있다. 일단 제대로된 model의 forward 과정이 이루어지기도 힘들고 ReLU 함수의 도함수를 살펴보면 back propagation도 제대로 이루어질 수 없다는 걸 쉽게 알 수 있다.
Xavier 초기화는 어떨까?
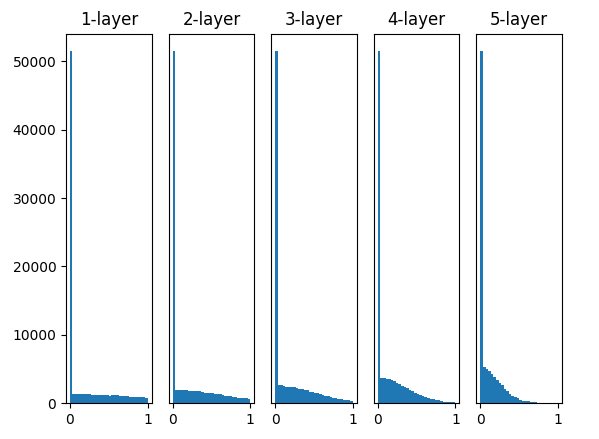
LeCun과 비교해보면 좋은 결과라고 생각할 수도 있다. 하지만 layer가 깊어질 수록 출력값이 0으로 근사하게됨을 확인 할 수 있다. 현재는 5층의 layer뿐이 없지만 요새의 모델 layer depth추세를 생각해보면 ReLU 활성화 함수와 xavier도 좋지 못한 조합이라고 생각된다.
그래서 등장한 초기화 방법이 바로 He 초기화 이다.
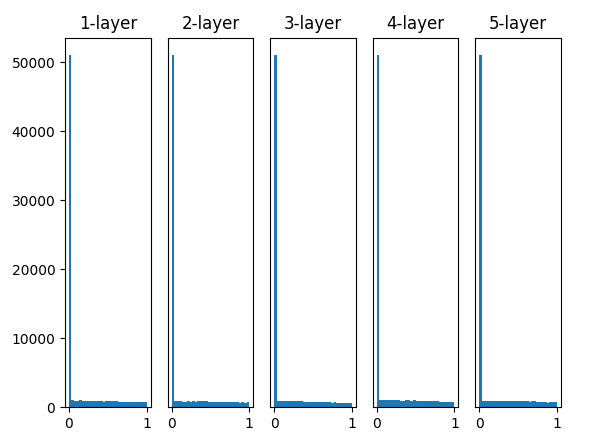
He 초기화의 결과를 보면 layer가 깊어진다고 해도 고른 분포를 보이고 있다. 즉 forward 과정에서도 문제없이 모델이 추론을 할 수 있게 된다는 의미이다.
나는 귀찮아서 극히 일부의 조합만을 테스트해봤지만 시간적 여유가 있으면 위의 github 링크에 들어가서 모든 조합을 테스트 해보는 것을 추천드린다
Outro
이번주부터 나와 가장 친한 캠퍼분과 함께 백엔드 프로젝트를 시작했다. 그동안 이론적인 공부만 해왔어서 코딩을 할 시간이 상대적으로 적었었다. 하지만 흔쾌히 프로젝트를 같이 하자고 해주셔서 좋은 기회를 얻게 된것 같다. 아마 백엔드 경험이 없으셔서 힘들고 재미없다고 느낄 수도 있겠다고 생각했지만 의외로 의욕도 넘치고 재미있다고 해주셔서 다행이었다. 나 또한 여태까지 대충 감으로만 해왔던 부분을 제대로 곱씹어 가면서 해볼 수 있었고 잊어버린 부분도 다시 상기시킬 수 있어서 매우 좋은 상호작용이라고 생각한다. 나는 협업을 할 때 있어서 가장 중요한 점이 상대방과의 fit이라고 생각하는데 나 혼자만의 생각일수도 있겠지만 나와 정말 잘 맞는것 같다. 프로젝트를 할 때 제일 위험한 것이 중간에 흐지부지 되는 것이라고 생각하는데 이번 프로젝트는 꼭 끝까지 완성을 해서 좋은 포트폴리오가 될 수 있으면 좋겠다고 생각한다:)
