Big-O Annotation

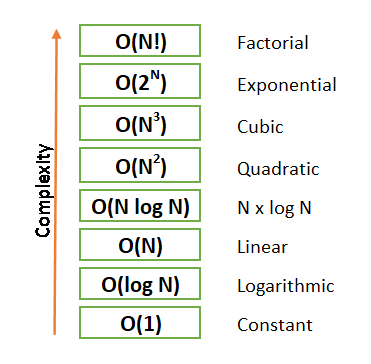
Big O 표기법은 Algorithm의 복잡도 혹은 성능을 표현하기위해 사용되며 수행시간을 기반으로 최악과 최선의 시나리오를 표현 할 수 있다.

각 Big O 표기법은 다음과 같다.

1. O(1)

void writeInOrder(int arr[]) {
	printf("%d", arr[0]);
}

O(1)은 입력갯수와는 상대적으로 일정한 시간을 유지한다. 입력 값이 1개든 100개든, 단 하나의 과정을 거치기 때문이다.

2. O(n)

void writeAll(int arr[], int size) {
	for(int i = 0; i < size; i++) {
    	printf("%d\n", arr[i]);
    }
}

예제와 같이 n의 개수대로 n번을 출력해야 된다. 개수가 증가 할 때 마다 시간도 균일하게 증가한다.

3. O(n²)

void writeAllPairs(int arr[], int size) {
	for(int i = 0; i < size; i++) {
    	for(int i = 0; i < size; i++) {
        	printf("%d = %d\n", arr[i], arr[j]);
        }
    }
}

두개의 loop이 존제하고 각 loop당 n번씩 반복된다. 그러므로 n²가 정립된다. 그래프에서 볼수 있듯이 비효율적인 성능을 갖고있다.

4. O(2ᴺ)

void fibonacci(int num) {
	if(num <= 1) return num;
    return fibonacci(num - 2) + fibonacci(num - 1);
}

Fibonacci의 반복적 계산을 예로 들수있다. 입력 값의 수가 더해질때 마다 계산의 복잡성은 두배로 증가된다. O(n²)에 비해 더욱 더 급격히 증가되는걸 볼수있다.

지금 까지 Big O에 대해 간단한 예제와 함께 알아보았다. 이외 O(log n), O(n log n)과 같은 logarithmic에 관하여 다음 포스팅에서 이진법 검색과 같은 예제와 함께 알아 보도록하겠다.