Algorithm&DataStructure
1.Big-O Annotation
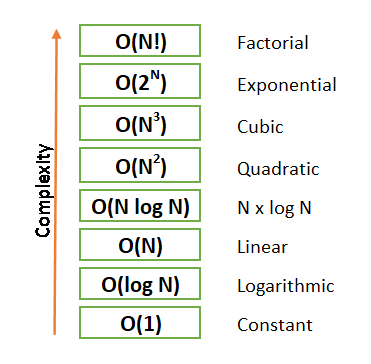
Big O 표기법은 Algorithm의 복잡도 혹은 성능을 표현하기위해 사용되며 수행시간을 기반으로 최악과 최선의 시나리오를 표현 할 수 있다. 각 Big O 표기법은 다음과 같다. O(1) O(1)은 입력갯수와는 상대적으로 일정한 시간을 유지한다. 입력 값이 1
2.Linear Search 순차(선형) 검색
.png)
Linear Search 순차(선형) 검색 순차(선형) 검색은 단순히 처음부터 끝까지 순차적으로 검색하는 것이며 O(n)의 시간복잡도를 갖고 있다. .png) Python 예제: 먼저 겁색 할 값을 x로 지정해준다. 그리고 x 값을 arr 배열에 있는 값들과 순서
3.Binary Search 01

이분 검색은 반복적으로 배열을 나누어가며 불필요한 값들을 미리 제거하며 겁색 범위를 좁혀 나가며 원하는 값을 찾아나간다. 이분 검색은 O(log n)의 시간 복잡도를 갖고있다.Python 예제:찾고자 하는 값을 배열의 중간 값과 비교한다. 만약 배열의 값이 크면 배열의
4.Stack 스택 & Queue 큐
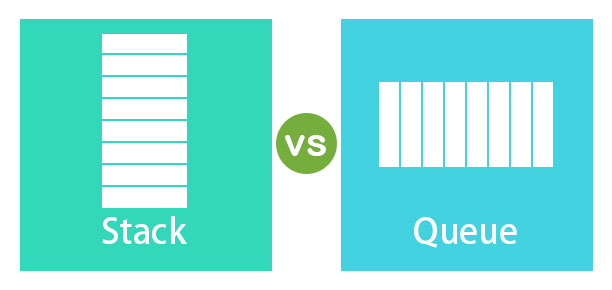
스택은 말그대로 쌓다라는 뜻으로 간단하게 데이터를 쌓아놓는다고 생각하면 된다. 예를 들어 박스를 일렬로 쌓아둘때 제일먼저 놓은 아래 박스는 제일 마지막으로 꺼낼수있듯이, 스택은 First In Last Out (FILO), 선입후출 자료구조이다.Python 예제:위에
5.Sort 정렬
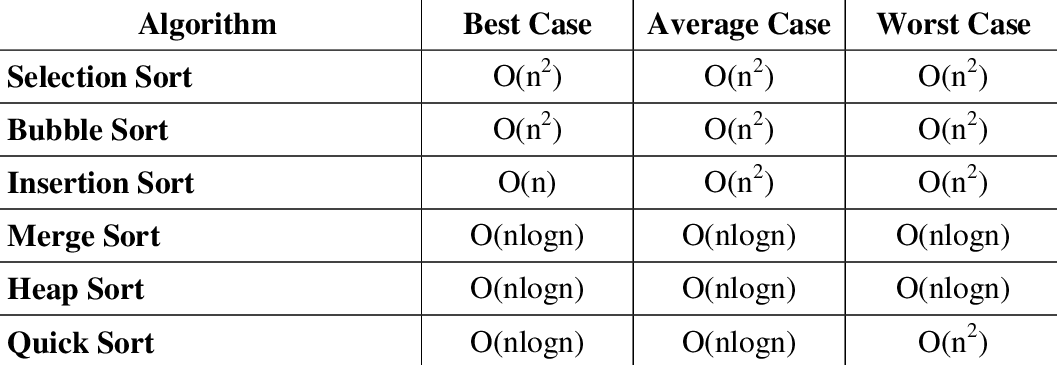
Selection Sort 선택 정렬 선택 정열은 맨앞의 값을 시작으로 다음의 값과 비교하며 정렬하는 방법이다. n번 만큼 작은 값을 찾아 이동해야 하므로 O(n²)의 시간 복잡도를 갖고 있다. Python 예제: 예제와 같이 두 단계의 반복문으로 구현할수 있다.
6.DFS (깊이 우선 탐색)
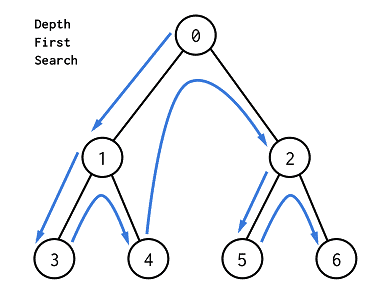
DFS는 Depth-First Search의 약자며 깊이를 우선적으로 탐색하는 알고리즘이다. DFS는 Stack 자료구조 혹은 Recursive function, 재귀함수를 이용한다. 위의 그림과 같이 0으로 시작하여 연결된 제일 작은 노드인 1 그리고 1과 연결된
7.BFS (너비 우선 탐색)
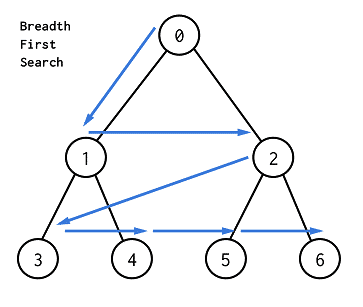
BFS는 Breadth-First Search의 약자이며 너비 우선으로 탐색하는 알고리즘이다. BFS는 Queue 자료구조를 이용한다. BFS는 첫번째 값과 인접한 노드의 값들을 먼저 queue에 넣어 처리후 그 다음 노드들을 똑 같이 탐색해 나간다. Python
8.Greedy Algorithm 탐욕법

탐욕법은 현재 상황에서 당장 눈 앞에 좋은 것만 고르는 방법을 의미한다. 탐욕법 문제 해결을 위해 단순히 제일 좋아보이는 것을 반복적으로 선택해도 최적의 결과를 구할 수 있는지 분석해야한다. 위의 Tree를 기반으로 위에서 부터 아래로 최대 합을 구해야한다고 가정
9.Binary Search 02

Binary Search