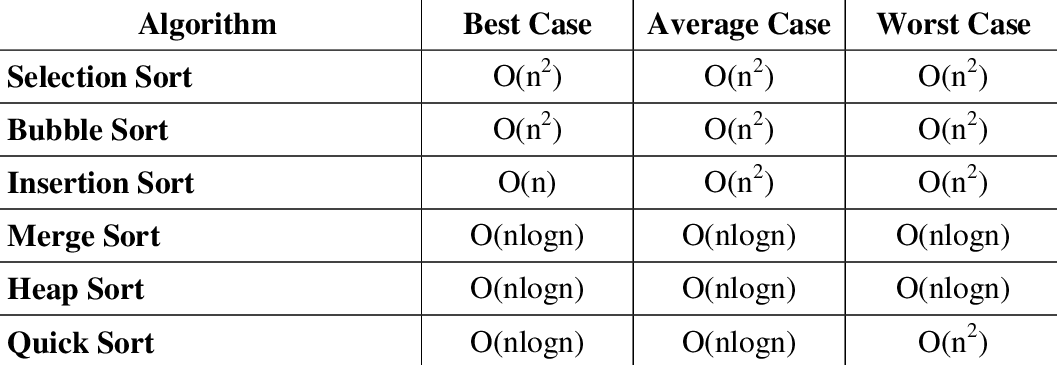
Selection Sort 선택 정렬
선택 정열은 맨앞의 값을 시작으로 다음의 값과 비교하며 정렬하는 방법이다.
n번 만큼 작은 값을 찾아 이동해야 하므로 O(n²)의 시간 복잡도를 갖고 있다.
Python 예제:
A = [7, 4, 5, 9, 8, 2, 1]
for i in range(len(A)):
min_idx = i
for j in range(i+1, len(A)):
if A[min_idx] > A[j]:
min_idx = j
A[i], A[min_idx] = A[min_idx], A[i]
print(A),예제와 같이 두 단계의 반복문으로 구현할수 있다.
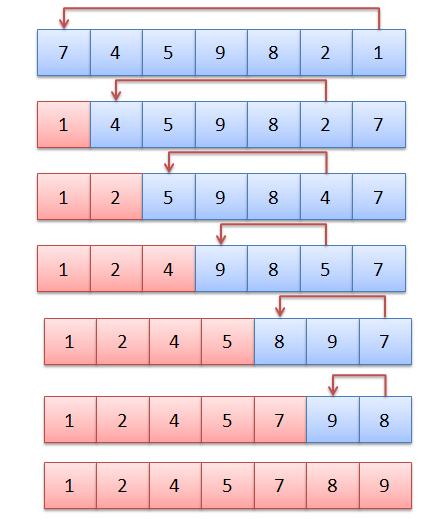
먼저 제일 첫번째 인덱스에 있는 7과 나머지 인덱스에 있는 값을 비교하여 제일 작은 값인 1을 앞으로 보낸다.
그리고 다음 2번쩨 인덱스에 있는 4를 비교해가며 4보다 작은 값인 2와 자리를 바꾼다.
이와 같은 과정을 계속 반복하여 배열을 정렬해 나간다.
Shell Sort 쉘 정렬
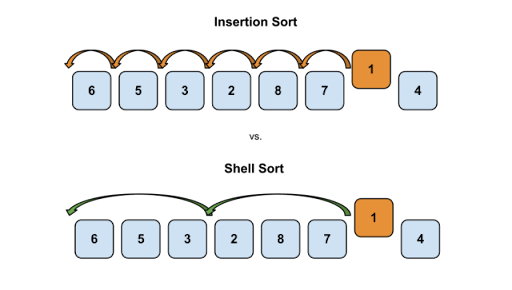
쉘 정렬은 삽입 정렬의 한 종류이며 O(n²)의 시간 복잡도를 갖고있다.
삽입 정렬은 한단계 당 한번의 비교와 이동이 있었다면 쉘 정렬은 한번에 여러 값들을 비교하며 정렬해 나갈 수 있다.
Python 에제:
def shellSort(arr):
# "GAP" 틈새를 만든다. => 배열을 반으로 나누어 시작점을 만든다.
gap = len(arr) // 2
while gap > 0:
i = 0
j = gap
# 마지막 인덱스인 j 까지 오른쪽과 왼쪽배열을 확인한다.
while j < len(arr):
if arr[i] >arr[j]:
arr[i],arr[j] = arr[j],arr[i]
i += 1
j += 1
# i번째 인덱스 부터 정렬되지 않은 값을 이동 시킨다.
k = i
while k - gap > -1:
if arr[k - gap] > arr[k]:
arr[k-gap],arr[k] = arr[k],arr[k-gap]
k -= 1
gap //= 2
arr = [12, 34, 54, 2, 3]
shellSort(arr)
print(arr)Bubble Sort 버블 정렬
버블정렬은 O(n²)의 시간복잡도를 갖고 있다.
Python 예제:
def bubbleSort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n-i-1):
if arr[j] > arr[j+1] :
arr[j], arr[j+1] = arr[j+1], arr[j]
arr = [-2, 45, 0, 11, -9]
bubbleSort(arr)
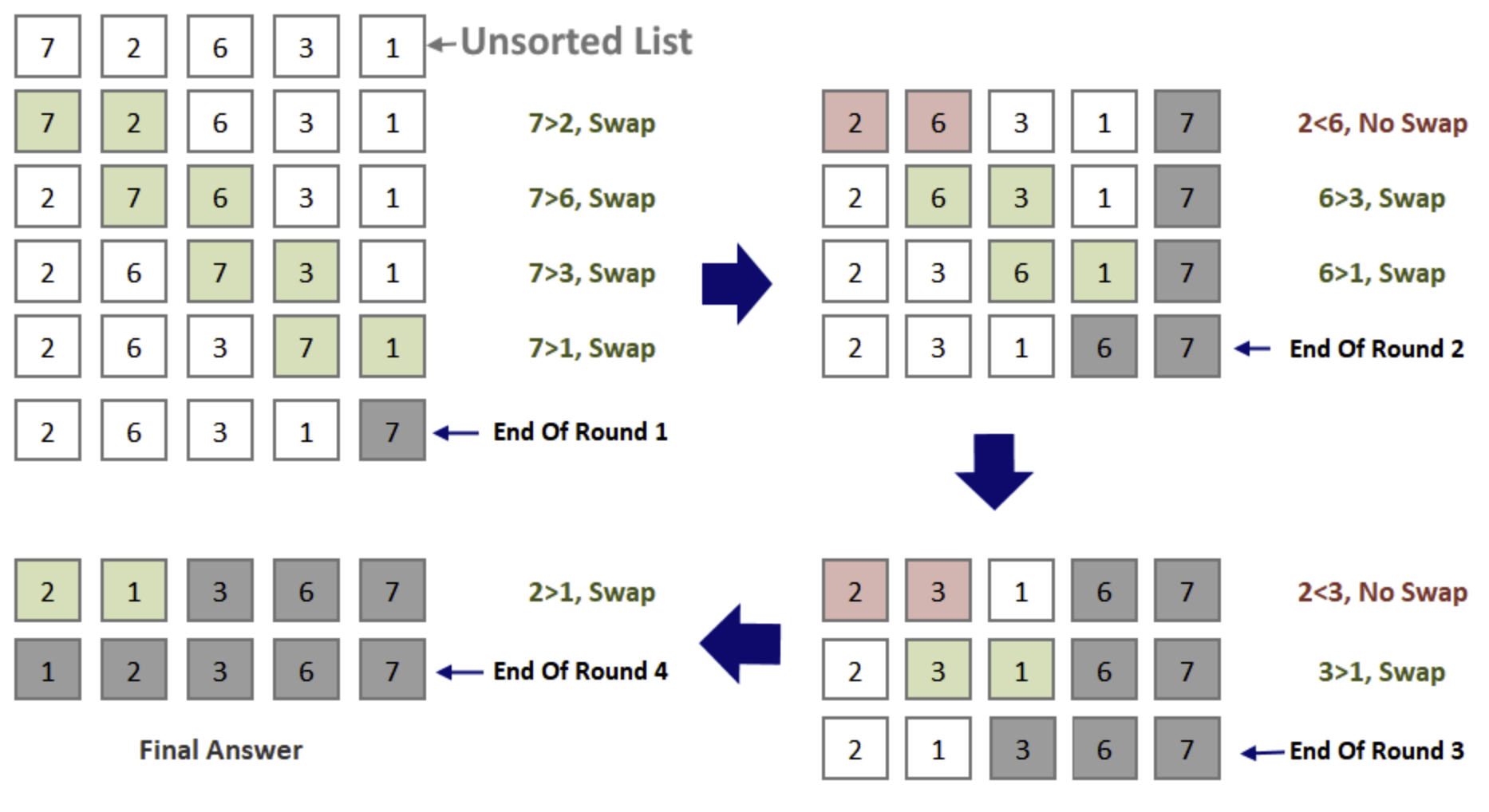
print (arr)먼저 첫번째와 두번째 인덱스을 비교하여 둘 중 작은 값을 앞으로 보낸다.
다음으로 두번째 인댁스와 세번째 인덱스 값을 비교하고 둘 중 작은 값을 앞으로 보낸다.
이와 같은 과정을 정렬이 될때까지 계속해서 반복한다.
Insertion Sort 삽입 정렬
삽입정렬은 최고 O(n) 그리고 최저 O(n²)의 시간복잡도를 갖고있다.

Python 예제:
def insertionSort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i-1
while j >= 0 and key < arr[j] :
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
arr = [9, 7, 6, 15, 17, 5, 10, 11]
insertionSort(arr)
print (arr)먼저 첫번째 인덱스 값인 9가 정렬 되어있는 가정하에 다음 인댁스 값인 7을 왼쪽 값인 9와 비교하여 작은 값을 앞으로 이동시킨다.
첫번쩨 인덱스로 이동한 7과 다음 인덱스 값인 6을 비교하여 작은 값인 6을 다시 첫번쩨 인덱스로 이동한다.
그리고 다음 인덱스의 값과 비교하고 작은 값과 자리를 바꿔가며 정렬해 나간다.
Merge Sort 합병 정렬
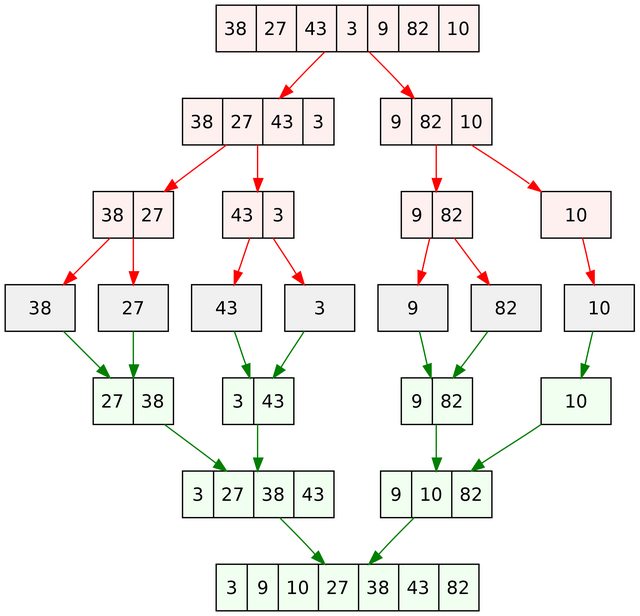
합병정렬은 배열를 나누고 서로 비교하여 정렬하며 O(nlogn)의 시간 복잡도를 갖고있다.
Python 에제:
def mergeSort(arr):
if len(arr) > 1:
# 배열을 반으로 나눈다.
mid = len(arr)//2
L = arr[:mid]
R = arr[mid:]
# 왼쪽 배열을 다시 반으로 나눈다.
mergeSort(L)
#오른쪽 배열을 다시 반으로 나눈다.
mergeSort(R)
i = j = k = 0
# 임시 배열에 값을 저장해 둔다.
while i < len(L) and j < len(R):
if L[i] < R[j]:
arr[k] = L[i]
i += 1
else:
arr[k] = R[j]
j += 1
k += 1
while i < len(L):
arr[k] = L[i]
i += 1
k += 1
while j < len(R):
arr[k] = R[j]
j += 1
k += 1
# 정렬된 배열 출력.
def printList(arr):
for i in range(len(arr)):
print(arr[i], end=" ")
print()
if __name__ == '__main__':
arr = [38, 27, 43, 3, 9, 82, 10]
mergeSort(arr)
print("정렬된 배열: ", end="\n")
printList(arr)먼저 배열을 나누어준다.
이때 하나 혹은 두개의 값으로 짝을 이루어 준다.
그리고 각 짝의 값을 비교하여 작은 값을 첫번째 인덱스로 지정해 준다.
짝을 이루고 있는 배열들을 비교해 가며 작은 값 부터 배열을 만들어 준다.
위와 마찬가지으로 하나의 배열로 비교하여 정렬해준다.
Heap Sort 힙 정렬
힘 정렬은 O(nlogn)의 시간 복잡도를 갖고있다.
힘 정렬전 먼저 주어진 배열을 Heapify를 통해 Max Heap으로 변환 시켜주어야 한다.
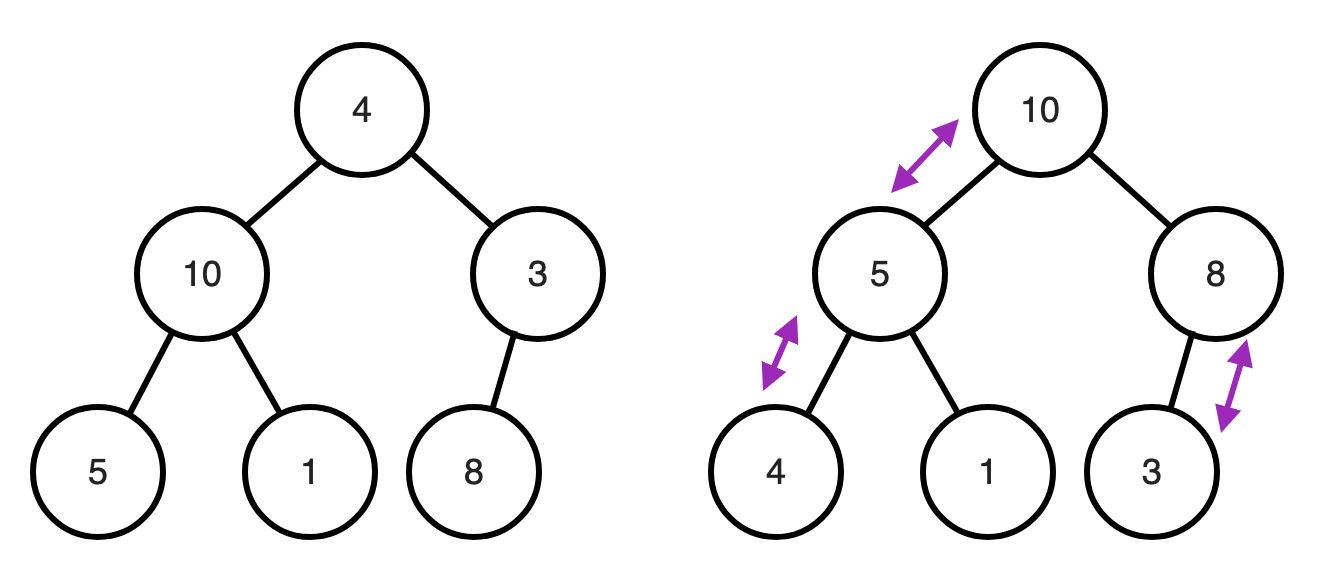
위의 다이아그램에서 '[4, 10, 3, 5, 1, 8]' 배열을 Binary Tree구조로 만든뒤 Heapify를 통해 Max Heap을 만들었다.
그리고 지금부터 힘 정렬를 시작 할 수 있다.
여기서 제일 큰 값인 10을 배열의 끝에 넣어주고 다음으로 큰 값인 8을 위로 이동 시킨다.
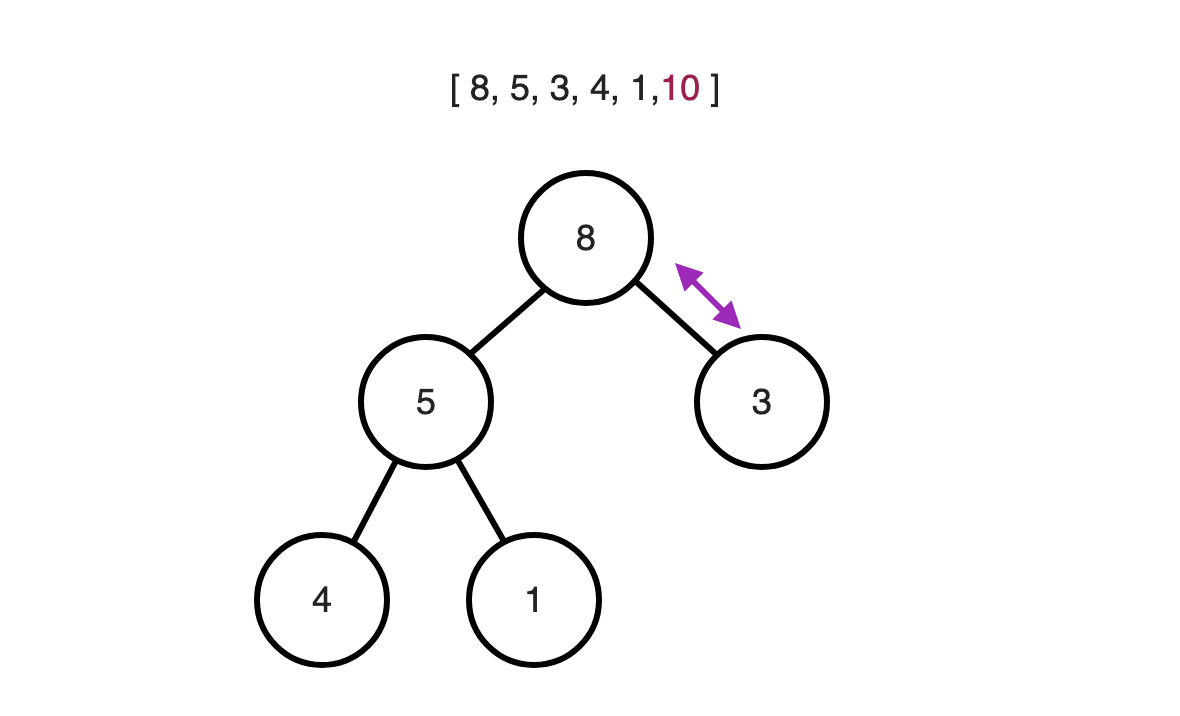
다음으로 8을 배열에 넣어주고 다시 Heapify를 통해 Tree에 있는 제일 큰 값을 위로 이동시킨다.
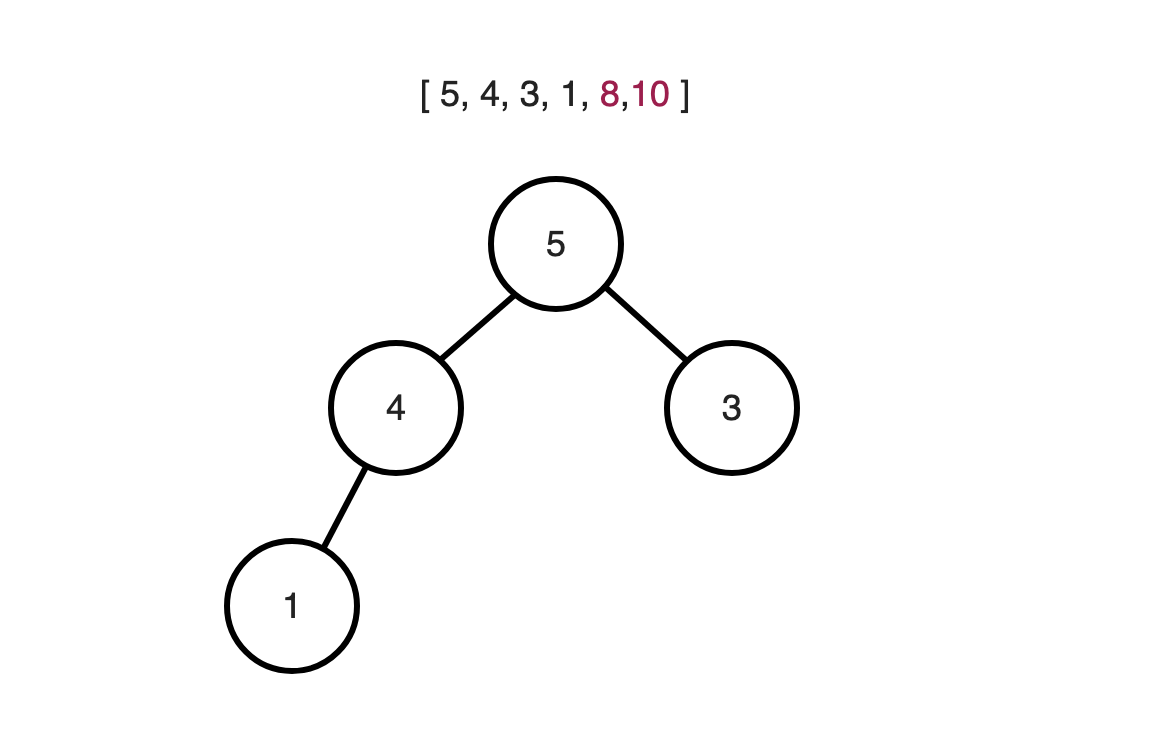
위와 같은 과정들을 반복하면 다음과 같은 결과가 나온다.
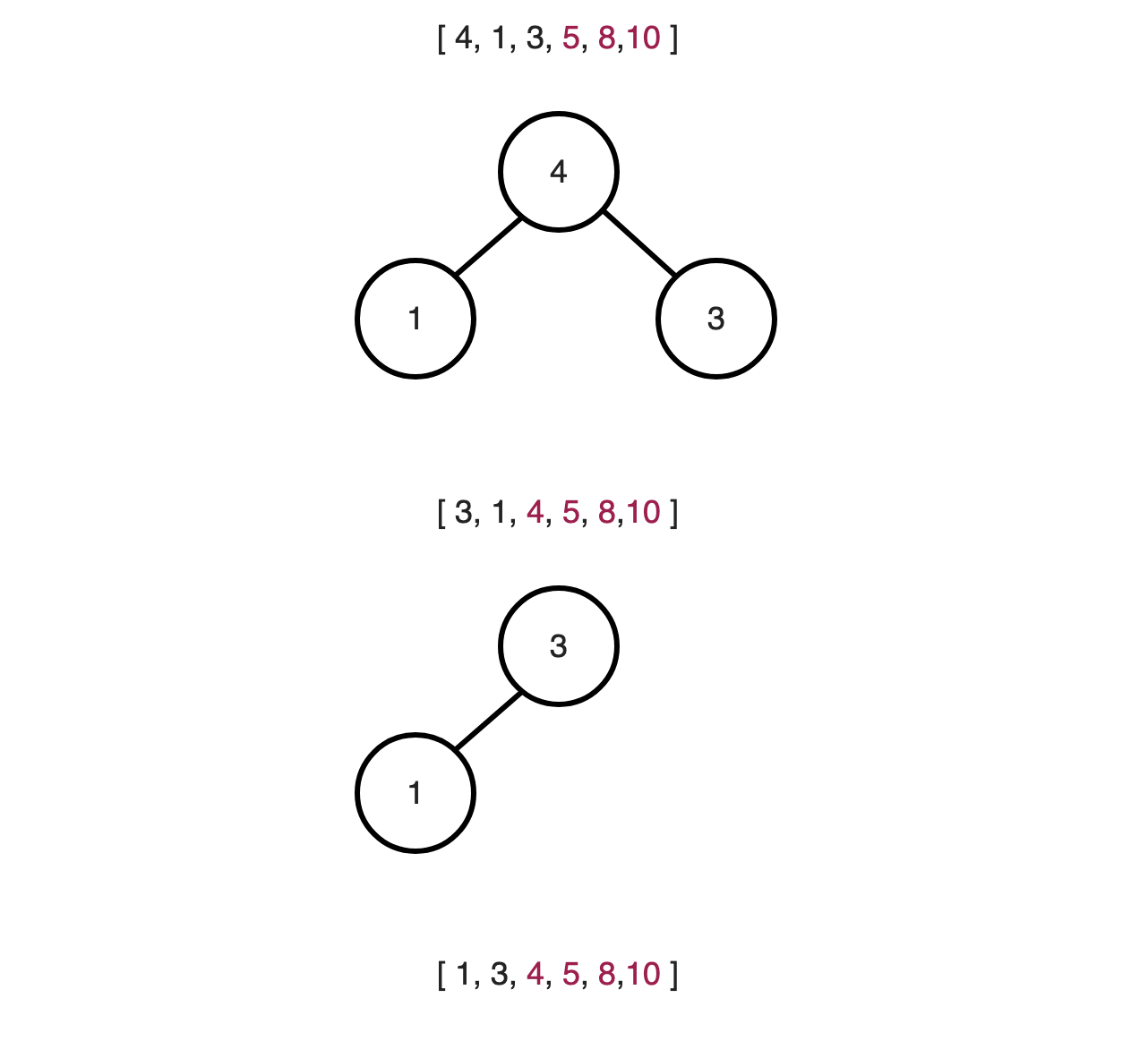
힘 정렬을 통해 위와 같이 [ 1, 3, 4, 5, 8, 10] 배열을 구성하였다.
✣ 참고로 힘 정렬은 Stable하지 않은 정렬 구조다.
Python 에제:
def heapsort(a):
def swap(a,i,j):
tmp = a[i]
a[i] = a[j]
a[j] = tmp
def siftdown(a, i, size):
l = 2*i+1
r = 2*i+2
largest = i
if l <= size-1 and a[l] > a[i]:
largest = l
if r <= size-1 and a[r] > a[largest]:
largest = r
if largest != i:
swap(a, i, largest)
siftdown(a, largest, size)
def heapify(a, size):
p = (size//2)-1
while p>=0:
siftdown(a, p, size)
p -= 1
size = len(a)
heapify(a, size)
end = size-1
while(end > 0):
swap(a, 0, end)
siftdown(a, 0, end)
end -= 1
arr = [1,3,2,4,9,7]
heapsort(arr)
print(arr)Quick Sort 퀵 정렬
퀵 정렬은 최대 O(nlogn) 그리고 최소 O(n²)의 시간 복잡도를 갖고있다.
✣ 참고로 퀵 정렬은 Stable하지 않은 구조다.
퀵 정렬에서는 Pivot 값을 지정해 줘야한다.
Pivot 값은 정렬의 기준범이 되어 Pivot 값보다 작으면 왼쪽으로 그리고 크면 오른쪽으로 배치된다.
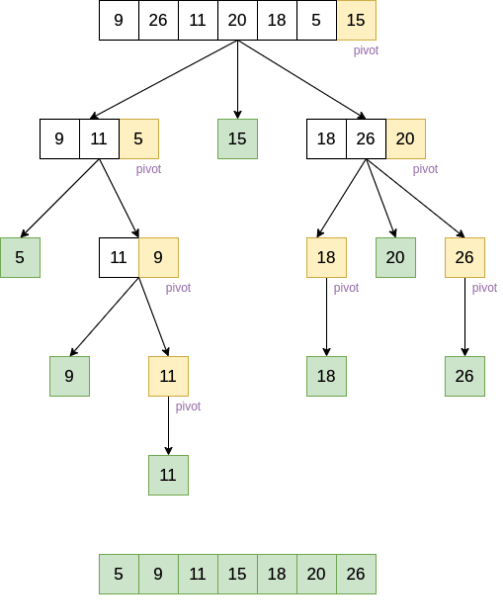
Python 예제:
def partition(start, end, array):
# Pivot 값 설정.
pivot_index = start
pivot = array[pivot_index]
# Pointer가 서로 넢어갈때 Pivot 값을 다시 설정한다.
while start < end:
# Pivot 값이 자신보다 큰 값을 찾을때까지 Start Pointer를 움직인다.
while start < len(array) and array[start] <= pivot:
start += 1
# Pivot 값이 자신보다 작은 값을 찾을때까지 End Pointer를 움직인다.
while array[end] > pivot:
end -= 1
# Start와 End Pointer가 서로 넢지 않았을 경우 서로의 값을 바꾼다.
if(start < end):
array[start], array[end] = array[end], array[start]
# Pivot 값을 End Pointer의 값과 교환 한다.
array[end], array[pivot_index] = array[pivot_index], array[end]
def quick_sort(start, end, array):
if (start < end):
# p = Partition Index
p = partition(start, end, array)
# Partition 전과 후에 정렬.
quick_sort(start, p - 1, array)
quick_sort(p + 1, end, array)
array = [ 9, 26, 11, 20, 18, 5, 15 ]
quick_sort(0, len(array) - 1, array)
print(arr)