1. Dijkstra 알고리즘
맞다. 그 유명한 다익스트라 알고리즘이다. 최단거리를 찾아가는 과정이다. 그리디 알고리즘의 한 종류이기도 하다.
다익스트라라는 네덜란드 프로그래머가 20분동안 심심풀이로 암스테르담에서 다른역까지 가는 최단거리를 계산하려고 끄적이다가 만들어낸 알고리즘인데 전세계적으로 굉장히 많이 사용되는 알고리즘이 되어버렸다. 대단허다 진짜 ㅋㅋㅋ
이 알고리즘은 기본적으로 weighted graph여야 한다. 최단거리를 계산해야하므로 edge에 값이 부여되야 할 수 밖에 없다.
그래서 A->E 로 가는 최단거리를 찾는다고 할때 각각의 과정 (A->D / D->E) 에서 걸리는 거리를 계산해야할 수 밖에 없다. 그리고 이 알고리즘이 대단한 이유가 또 있다. A->E로 가는 최단거리를 구하게 되면 그와 동시에 모든 노드에서 A로가는 최단거리가 함께 발견이 된다.
그럼 실행 과정을 일단 살펴보자.
2. 알고리즘 실행 과정
먼저 그래프를 만들어 보자. 이번엔 weight(거리,edgeValue)를 추가해야하므로 add할때 obj를 push해야한다.
class Weighted {
constructor() {
this.adjacencyList = {};
}
addVertex(val) {
if (!this.adjacencyList[val]) {
this.adjacencyList[val] = [];
}
}
addEdge(v1, v2, weight) {
this.adjacencyList[v1].push({ node: v2, weight });
this.adjacencyList[v2].push({ node: v1, weight });
}
// 나머지 메소드는 거의 비슷해서 생략하겠다
}
var weightedGraph = new Weighted();
weightedGraph.addVertex("a");
weightedGraph.addVertex("b");
weightedGraph.addVertex("c");
weightedGraph.addVertex("d");
weightedGraph.addVertex("e");
weightedGraph.addVertex("f");
weightedGraph.addEdge("a", "b", 4);
weightedGraph.addEdge("a", "c", 2);
weightedGraph.addEdge("c", "d", 2);
weightedGraph.addEdge("c", "f", 4);
weightedGraph.addEdge("b", "e", 3);
weightedGraph.addEdge("d", "e", 3);
weightedGraph.addEdge("d", "f", 1);
weightedGraph.addEdge("e", "f", 1);그리고 각각 vtx를 추가하고 weight를 설정해주면 아래와 같은 그림이 된다.
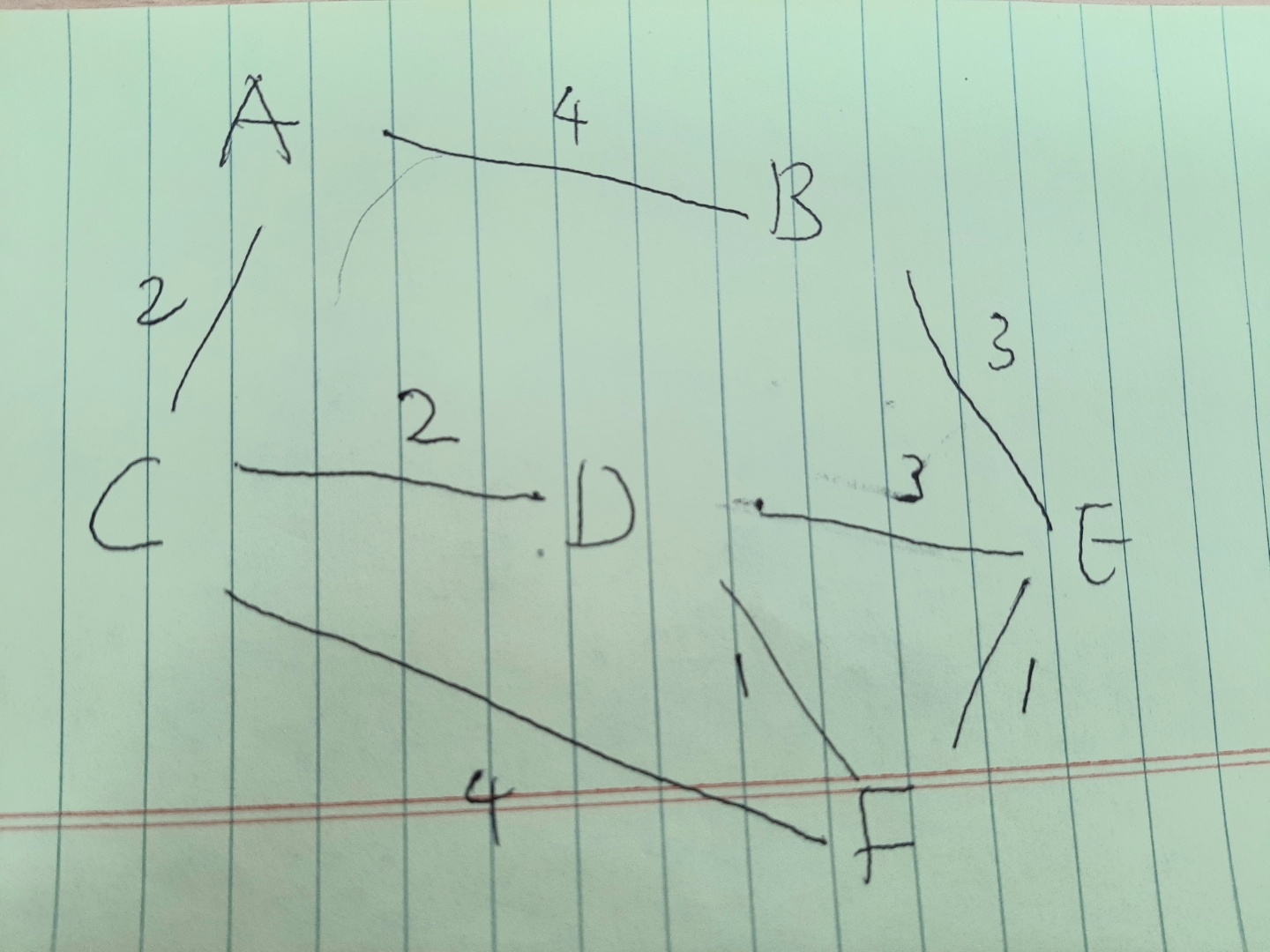
그리고 A에서 E로가는 최단거리를 구해본다고 하자. 어떤 알고리즘을 거쳐야 할까?
우선 영어로 된 접근방법을 살펴보자.
-
The Approach
-
First we choose start point and destination.
-
Every time we look to visit a new node, we pick the node with the smallest known distance to visit first. (using priority queue dequeue)
-
After we chose which node to visit, we mark the node as visited.
-
Once we’ve moved to the node we’re going to visit, we look at each of its neighbors.
-
For each neighboring node, we calculate the distance by summing the total edges that lead to the node we’re checking from the starting node.
-
If the new total distance to a node is less than the previous total, we store the new shorter distance for that node. and we also update very previous node to that node to get to the starting point. (update only if we find the shortest way).
-
Keep doing until what we picked up is desitination node.
-
-
첫번째로 출발점과 도착점을 고른다.(A->E)
-
A를 Visited에 추가하고 A와 이웃사이의 거리를 계산해서 Distance 표에 추가한다.
-
이미 추가된 거리보다 새로 계산된 거리가 적을경우:
- Distance에 새로운 거리를 업데이트한다.
- 그리고 Previous에 A로 가기 위해서 거쳐야할 바로 노드중에 바로 이전의 노드를 업데이트한다.
-
그리고 다시 노드를 선택하는데 이때 Distance 표에서 가장 거리가 적은 것을 선택한다.
-
선택된 노드의 이웃과 A사이의 거리를 계산한다.
-
위의 과정 반복. 언제까지? E를 뽑을 때까지.
3. 표로 살펴보기.
역시 표로 살펴보자.
먼저 Visted/Distance/Previous 세 가지 obj를 만들어야 한다.
우선 A는 시작점이므로 visted에 추가해주고 거리는 0이다. 그리고 나머지 distance는 일단 Infinity로 설정해두고 previous도 모두 null로 정해두자.
그리고 A의 이웃은 B와 C이므로 B와 C로부터 A의 거리를 측정한다.
모두 distance는 이미 등록된 거리보다 적으므로 distance에 업데이트 하고 previous에도 업데이트한다.
그리고 나서 distance를 보면 가장 starting vtx제외하고 가장 적은 거리가 C이다. 그럼 C를 선택한다.
C를 visited에 저장하고 C의 이웃을 살펴본다. 그럼 A는 이미 방문했으니까 D와 F의 거리만 측정하면 됨.
D와 F의 최단거리는 C를 거쳐서 A로 가는 거리가 각각 4,6이다. 그럼 또다시 distance에 등록된 최단거리와 비교해서 적으면 업데이트 함. 그리고 previous에도 업데이트 한다. 이번엔 A로 가기위해 거쳐야할 VTX중 바로 전의 VTX는 C이다. 그래서 C를 등록해두자.
그리고 방문하지 않은 노드중에서 distance에서 가장 적은 숫자는 B와 D인데 B부터 하자.
visited에 B를 추가하자. 그리고 이웃을 보면 A와E인데 A는 이미 방문했으므로 E만 방문하면 된다.
E에서 B를 통해 A로 가는 최단거리는 7이다. 그럼 distance에 등록된 E를 살펴보자. Infinity이므로 7이 더 작다.
따라서 distance와 previous에 등록하고 distance에서 가장 작은 숫자를 찾자. D이다. D를 visited에 넣고 이웃들을 보자.
C,E,F이다. 이중에 visited에 없는 노드는 E,F이다. D를 거쳐서 A로 가는 최단거리를 구하자. 그럼 E는 7이나오고 F는 5가 나온다. distance와 비교했을때 E는 이미등록된 거리가 7이라서 continue한다. 반면 F는 6이기 때문에 distance와 previous를 업데이트한다.
이런식으로 뽑은 NODE가 destination 즉 E가 될때까지 진행한다. 그럼 아래와 같은 표가 완성된다.
var visited = [A, C, B, D, F];| Vtx | Shortest path from A |
|---|---|
| A | 0 |
| B | |
| C | |
| D | |
| E | |
| F |
| Vtx | Previous Node to get to A |
|---|---|
| A | null |
| B | |
| C | |
| D | |
| E | |
| F |
그래서 E로 가는 최단거리는 6이고 거쳐야한 VTX는 previous를 보면된다. E->F->D->C->A 가 된다. 이걸 reverse하면 된다.
처음 접할때는 굉장히 복잡해서 직접 손으로 그려가면서 여러번 해보는과정이 꼭 필요하다. 그럼 익숙해진다. 언제나 그렇듯.
그럼 다음글에서 실제 코드를 작성해보자.
