1. 순열 구하기

순열은 nPr로 나타낸다. n개의 숫자중에서 r개의 숫자를 뽑는 경우의 수이다. 순서를 신경쓴다. 공식은 n!/(n-r)! 이다.

이번엔 arr를 주고 여기서 r개를 뽑아서 나오는 경우의 수를 만들어볼려고 한다. 그래서 순열뿐만 아니라 순열 각각의 조합을 또다시 구해볼 수 있다.

재귀로 어떻게 나타낼 수 있을까?

2. 접근 방법

• pseudocode
  • ch배열을 만든다.
  • dfs 재귀를 만든다.
  • for문을 만든다.
  • level+1을 pass하는데 하기 전에 ch에 해당 index를 체크한다.
  • level이 r이 되면 answer에 넣는다
  • ch를 푼다.
  • 다음for 문을 실행한다.

부분집합이랑 비슷한 로직이다. 뽑은것은 체크하고 answer에 넣은다음 풀면된다.

function permutation(r, arr) {
  let answer = [];
  let ch = Array.from({ length: arr.length }, () => 0);
  let temp = Array.from({ length: arr.length - 1 }, () => 0);

  function dfs(level) {
    if (level === r) {
      // deep copy
      // 완전히 새로운 temp를 다시 return해서 push해야함.
      // 안 그럼 push할때마다 answer안에 있던 temp가 마지막 push한 temp로 바뀜. 주소가 같으므로
      // 그래서 완전히 새로운 주소를 가진 temp를 push하는 깊은 복사를 해야 함
      // slice는 완전 새로운 array를 리턴하므로 answer안에 있는 temp들은 같은 주소를 공유하지 않음.
      answer.push(temp.slice());
    } else {
      for (let i = 0; i < arr.length; i++) {
        // 같은 종류의 숫자를 조합하지 않기 위함 임.
        // ch[] 에서 1이 있는 위치는 빼고 나머지 위치에 있는 것들을 arr에서 뽑아서 temp에 집어넣음
        if (ch[i] === 0) {
          ch[i] = 1;
          temp[level] = arr[i];
          dfs(level + 1);
          ch[i] = 0;
        }
      }
    }
  }

  dfs(0);

  return answer;
}

temp = [1] 
temp = [1,2]
temp = [1,2,3] push

temp = [1,3,3]
temp = [1,3,2] push
... 

이런식으로 쌓인다.

여기서 ch 배열은 개발자도구에서 permutation함수에 break point를 걸어서 직접 보는게 이해가 빠를 것이다.

트리로 한번 재귀를 표현해보았다.

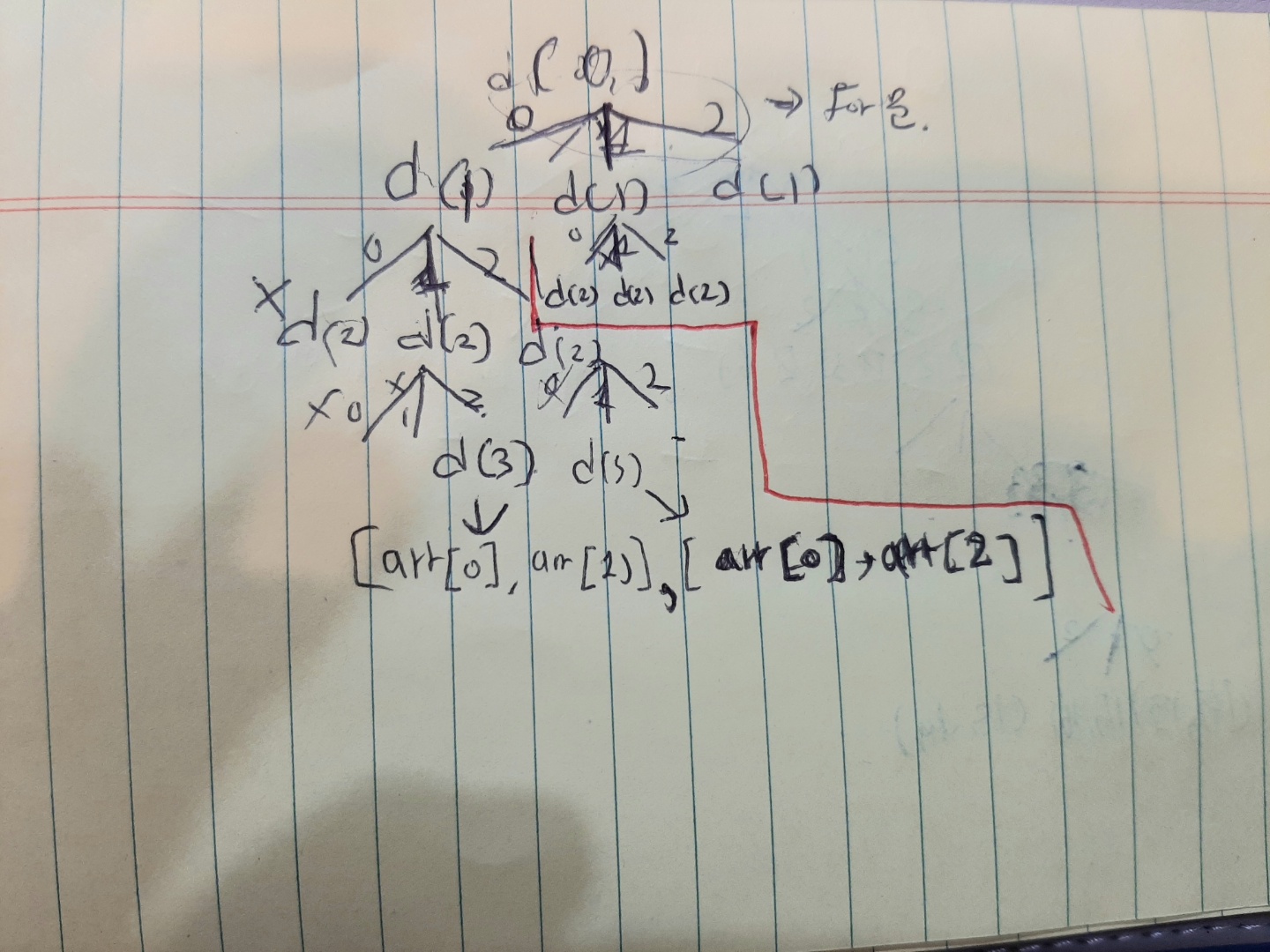
P.S: deep copy를 추가로 또 알아두자!