1. 조합

조합은 순서 상관없이 n개의 숫자중에 r을 뽑는것을 말한다. 다시 말해, 1,2,3 이 주어지면 1,2 / 1,3 / 2,3 이렇게 조합을 구할 수 있다. 1,2 / 2,1은 같은거라고 본다. (순열은 다른거라고 본다.)

따라서 nCr = nPr / r! 라고도 말할 수 있다.

또는, 논리적으로 생각해보자! [1,2,3,4,5] 에서 3개의 수를 뽑는다고 가정하면 2가지로 나뉠 수 있다. 5를 기준으로 잡았을때 5가 포함되어있는경우와 없는 경우로 나뉠 수 있다. 5가 포함되는 경우는 [1,2,3,4] 중에 2개를 뽑는 경우일 것이고 포함되지 않는 경우는 3개를 뽑는 경우일 것이다.

따라서 nCr = n-1Cr-1 + n-1Cr 로 표현 할 수 도 있다. 따라서 이런경우에는 재귀 트리로 나타낼 수가 있다.

5C3를 재귀 트리로 나타내 보자.

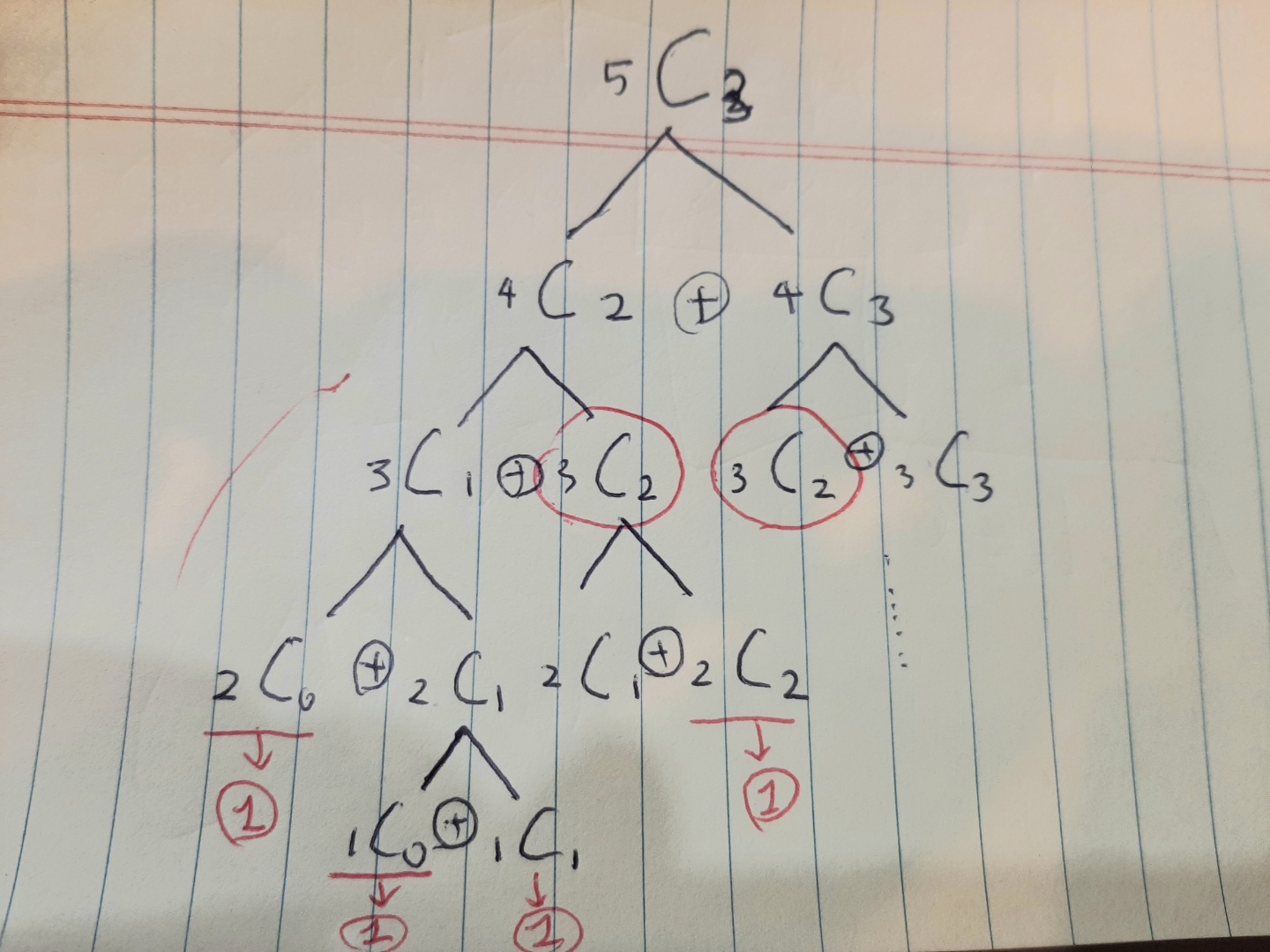
2. 접근방법

같은것은 메모해뒀다가 나중에 나타나면 써먹는다.

comb(n,r) 을 만들고 n === r || r === 0 이면 1을 리턴한다.

function combinationCases(n, r) {
  let memo = {};

  function dfs(num, pick) {
    if (memo[`${num}C${pick}`]) return memo[`${num}C${pick}`];
    if (num === pick || pick === 0) return 1;
    else
      return (memo[`${num}C${pick}`] =
        dfs(num - 1, pick - 1) + dfs(num - 1, pick));
  }

  return dfs(n, r);
}

그럼 다음엔 이 함수를 사용해서 수열을 추측하는 함수를 또 만들어보자! 재밌다 진짜 신기하다. 이런 논리로 무언가를 자동화하고 예측할 수 있다니.