Motivations 📚
- Previous research, NCSN, had a limitation in that it works well only in images of low resolution.
- In addition, the model was unstable under some settings.
- It is unclear how to define the noise scales.
- Langevin dynamics sampling methods fail or take a long time to converge in high-dimensions with an imperfect score network.
Contributions ⭐️
- They propose a method for choosing noise scales.
- The method for incorporating the noise information is proposed.
- They also propose for defining parameters of Langevin dynamics.
- Employing an exponenetial moving average (EMA) helps to improve the sample quality.
Method
There are a lot of design parameters which is much influential for training and inference of NCSNs.
- The set of noise scales
- The way that incorporates information of .
- The step size and the number of sampling steps per noise scale T of Langevin dynamics
너무 힘들어서 한글로 쓰겠음 ..
Choosing noise scales
Initial noise scale
When score network trained with single noise, high noise help the estimation of score functions, but also trigger corrupted samples. -> use different noise scales!
NCSN에서의 noise schedules는 geometry sequence로 정의되고 decreasing sequence이다 . 이전 연구에서는 로 정했었는데, 여기에서 로 지정한 것은 아주 작은 noise scale이 적용되기 때문에 reasonable하다 .
그렇다면 은 합당한 선택일까?
이를 이해하기 위해서는 이 하는 역할에 대해 생각해볼 필요가 있다.
Langevin dynamics를 통한 샘플링 시, 마지막 샘플들의 diversity는 에 크게 영향받는다.
큰 영향을 받는 이유는 1) 가장 큰 randomness (large variance)를 갖고, 2) intial state이기 때문이다. (내 생각에.)
하지만 의 값이 너무 크다면 다양한 noise scales를 보장해야하기 때문에 langevin dynamics 과정이 굉장히 expensive 해진다.
저자는 이를 수식적인 정의 및 분석으로 의 적정값을 도출해낸다.
우선 dataset 이 있다고 해보자. 그리고 dataset에서의 각 data들에 대한 empirical distribution을 따로 정의한다. 본 섹션에서의 목적은 일 경우에서의 분석이기 때문에 noise scale 에 대한 distribution과 이에 대한 에 대한 score function을 정의한다.
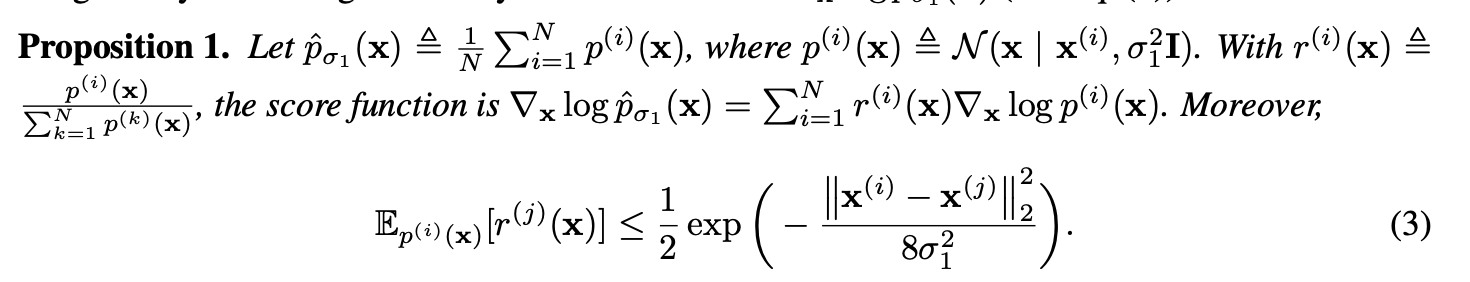
[Proof 1.]
저자는 위와 같은 proposition 1.을 정의한다. 에 대한 score function에 대한 정의인데, 자연스럽게 각 empirical distribution에 대한 score functions의 weighted sum으로 정의된다 (그냥 미분 정의에 의해서).
일단 diverse한 samples를 만들기 위해서는 initialization에 상관없이 강한 diversity를 보장해주면 된다. 본 식에서 diversity를 고려할 수 있는 것은 식 (3)의 이다. 이렇게 정의하는 이유는 어떤 임의의 i, j에 대해서 i->j로 transition 하는 경우 score function의 기여(coefficient )를 고려해주기 위함이다 (모든 j에 대해 생각해보자).
식 (3)을 보면 해당 bound는 pair xs 데이터의 euclidean distance와 에만 dependent하다. data pair야 주어지는 값이기 때문에 제어할 수 없으니, 파라미터로서 제어할 수 있는 부분은 만이 된다.
임의의 i,j에 대한 관계로서 정의된 (3)이기 때문에, 의 제곱에 비례하게 모든 j에 대한 i->j transition 시의 score function 내부의 기여가 커진다. 만약 data pair사이의 Euclidean distance보다 의 기여가 더 커진다면, initialization에 상관없이 diversity를 보장할 수 있다는 말이 된다.
물론 이 직관에 따라 diversity를 무작정 높게 주면 Langevin dynamics 과정의 complexity가 커지기 때문에 적정선을 제안해줘야한다.
이는, 모든 training data points의 pairs 사이의 maximum Euclidean distance를 기준으로 을 정해주면 된다.
이는 주어진 dataset에 맞춰진 수치를 정할 수 있게 된다는 말이 된다.
Other noise scales
지금까지 과정에서 의 값은 정해졌다. 그러면 이 중간 schedule은 어떻게 정해야할까
논문에서는 일단 geometric sequence 형태는 유지한다. 하지만 하나의 직관을 소개하는데, 이는 간단히 말하면 "인접한 scales의 점진적 변화 필요" 이다. 이게 무슨 말이냐면, 에서 생성된 많은 데이터 들은 의 high density regions에 존재해야한다는 것이다.
remind : NCSN에서는 sequence는 decreasing sequence이다. 즉, 의 noise scale이 의 noise scale보다 작다는 것이고, 라는 의미가 된다.
이 distribution사이의 overlap을 고려하기 위해 Gaussian distribution에 대한 괴랄한 식변형을 한다.
간단하게 말하자면, spherical coordinate로 표현하면 isotropic gaussian의 angular term은 말 그대로 등방성이라 무시가 가능하고, 그 외의 scale term만 고려하면 된다는 아이디어를 사용한다. 이렇게 되면 distribution처럼 표현할 수 있게 된다. ( distribution이라는건 아니다.)
왜 이렇게 표현할까? 위에서 언급했듯이, NCSN에서는 isotropic Gaussian distribution을 사용하고 이는 hypersphere처럼 생각할 수 있다. von Mises–Fisher distribution과 연관이 있다.
그러니까 영역간의 overlap을 고려하기 위해서는 spherical distribution으로 표현하여 angular term을 무시하고 radius term만 고려하는게 더 쉽다.
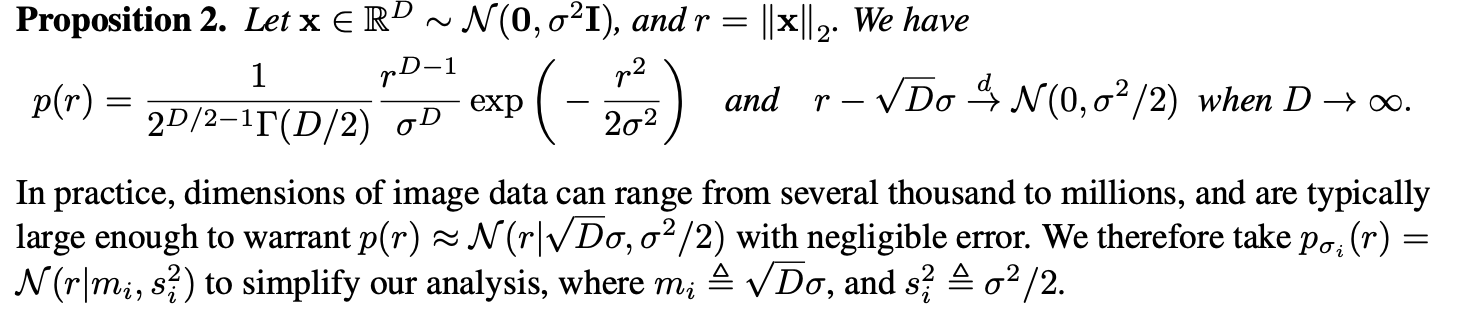
[Proof 2.]
위의 Proposition 2.가 이에 대한 정의이다. 여기에서 에 대한 내용은 Central limit theorem으로부터 유도된다 (in-distribution convergence).
이렇게 반지름 혹은 radial 파라미터 에 대한 variable로 두 distribution 사이의 overlap을 고려하면 되는 것이다.
상기하자면, 여기에서의 overlap은 로부터 생성된 많은 데이터들이 의 high density region에 존재해야한다는 것이다. 이를 위해 의 high density region을 로 정한다. 이는 heuristic한 직관에 따른 three sigma rule이라는 건데, 가설 검증이나 outlier 분석 등에 많이 사용되기도 하고 경험적인 법칙이라 설명은 넘어가겠다.
그리고 이렇게 정의된 high density region에 distribution이 많이 overlap 되면 된다.
[Proof 3.]
: CDF of standard gaussian
, geometric sequence라 모두 같다.
이 overlap은 이렇게 정의 된다. 여기에서는 이 overlap region의 값을 라는 설정된 큰 값으로 지정한다.
이 기준을 기반으로 geometric sequence의 값을 정할 수 있다. 이를 통해 schedule을 정의한다.
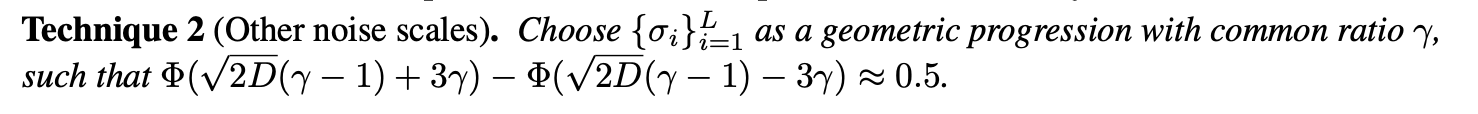
Incorporating the noise information
본 논문에서는 noise 를 어떻게 모델에 반영해야 하는지도 언급한다. 위의 결론에 따라 본 논문에서는 큰 을 설정할 수 있게 되었고, 이에 따라 noise scales의 수가 많아졌다. 이와 같이 훈련을 잘 하기 위해서는 굉장히 많은 noise 정보를 network에 주입시켜야 한다.
뿐만 아니라 NCSN에서 제안된 noise scale을 반영하는 방법은 normalization layer에 제공하기 때문에 network에 normalization layer가 존재해야만한다.
이러한 문제를 해결하기 위해 아주 간단한 방법을 제안하는데, 이는 가 에 비례했다는 이전 연구의 관찰과 3.2 section 에서 정립되었던 의 관계에서 아이디어를 얻는다.
위에서 언급했듯이, score function의 norm은 에 비례하므로 간단하게 unconditional score network 에 로 scaling 해주면 된다.
Configuring annealed Langevin dynamics
이전까지는 noise scales의 세팅에 대한 내용이었다. 해당 섹션들에서는 을 어떻게 지정할 수 있는지에 대한 것이었다. 본 섹션부터는 을 어떻게 세팅할 수 있는지에 대한 논의이다.
Reminder : DDPM과 다르게 NCSN을 위한 Langevin dynamics는 outer iteration / inner iteration으로 이루어진다. outer iteration은 inner iteration이 끝나고 그 다음 noise scale에 대해 langevin dynamics를 수행하는 것이고 noise scales의 수는 이다. inner iteration에서는 실질적인 Langevin dynamics를 수행하는 과정이고 iteration의 수는 로 정의된다.
TMI : 물론 이후 논문인 VESDE/VPSDE 논문에서는 Diffusion model의 sampling method는 확률론적 graphical model 그대로 도출해내서 예측하는 거라서 forward sampling / ancestral sampling - predictor으로 보고, Langevin dynamics는 예측된 값을 수정하는 과정인 corrector로 본다. 각 sampling method의 역할이 다르다고 할 수 있기에, 해당 논문에서는 두 방법 모두 쓴다.
우선 좋은 이 뭔지 생각해보기 전에, 어떤 Langevin dynamics가 좋은건지 생각해보자. 논문에서는 better mixing 이라는 말을 쓰는데, 결국 해당 step에서의 noise scale인 을 잘 반영하는게 목표인듯 싶다.
이게 무슨 말이냐면 에서 시작해서 의 distribution으로 보내는 것을 목적으로 하는 Langevin dynamics를 생각해보자. 본 상황에서 의 distribution은 을 따른다고 하자. 그럼 Langevin dynamics sampling process를 번 수행한 뒤의 distribution은 를 따르는게 좋다 (사전에 noise scales를 그렇게 정했으니까).
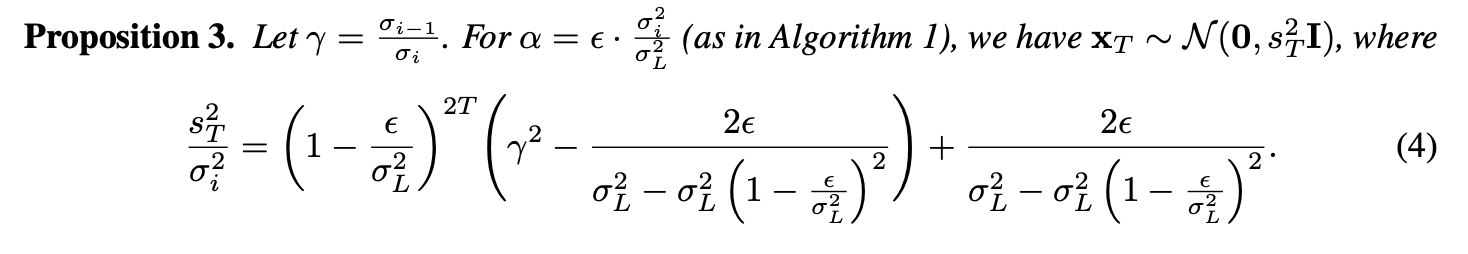
그럼 위에 들었던 예시를 그대로, 에서 시작해서 의 distribution으로 보내는 것을 목적으로 하는 Langevin dynamics를 생각했을때, 번 Langevin dynamics sampling process (inner iteration)을 거친 의 distribution 은 위의 Proposition 3.과 같이 정의 된다. [Proof 4.]
번 step 이후 distribution의 variance는 와 동일하는게 합당하므로, 위의 를 1이 되도록 설정해주면 된다. 이로부터 을 정의해주면 된다. 본 관계를 통해 두개의 파라미터를 정해줘야하기 때문에, 논문에서는 우선 를 computational budget에 맞게 설정한 후 을 설정하는 방법을 제안한다.
Improving stability with moving average
이 부분은 지극히 경험적인 내용이다. 저자들은 EMA ()를 sampling 시 적용했을때 훈련 안정성이 매우 좋아짐을 발견했다고 한다.
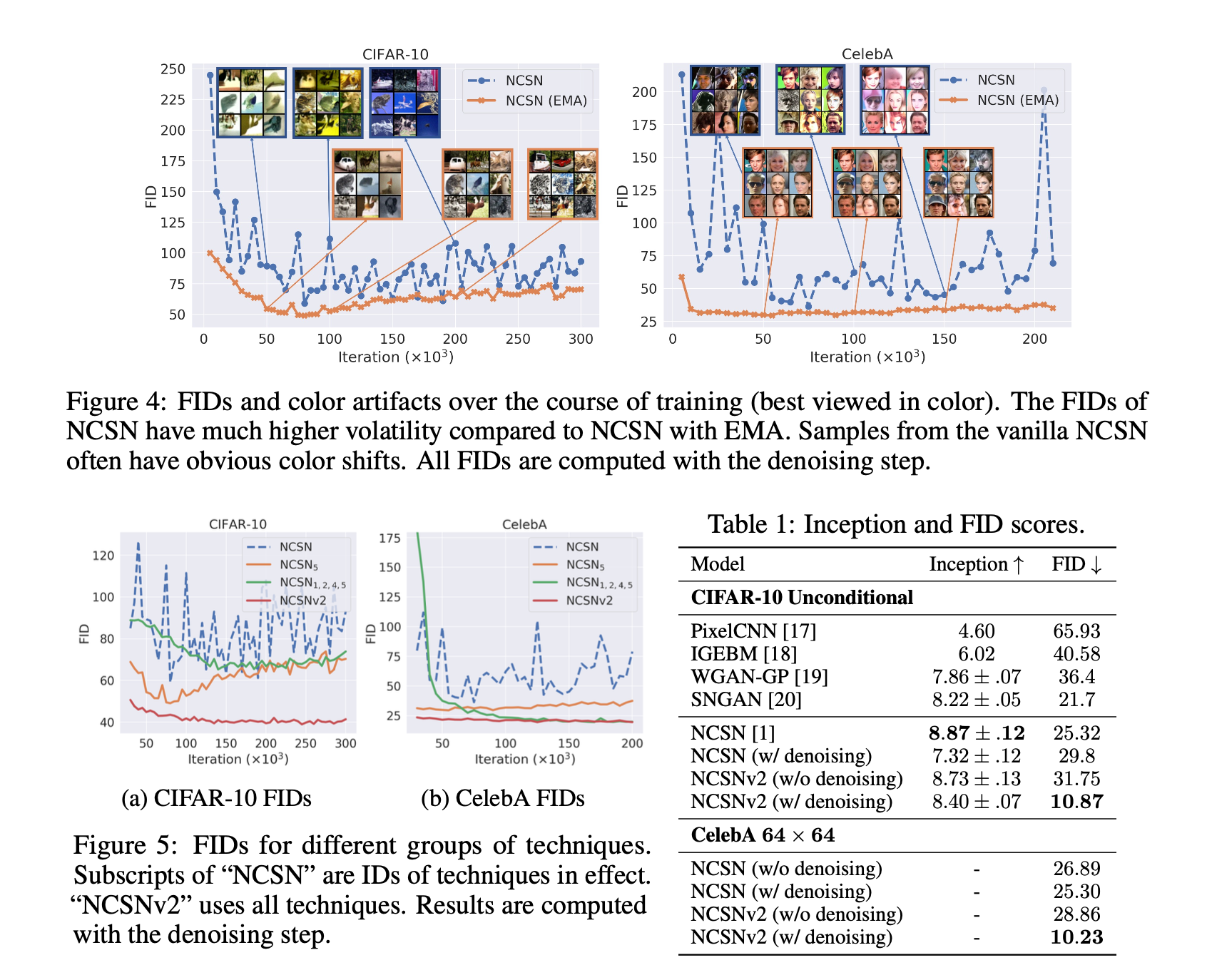
Experiments

Proofs
1. Proposition 1.

2. Proposition 2.

3.

4. Proposition 3.
