오늘은 sparse representation에서 근본 방법론이라 볼 수 있는 OMP(Orthogonal Matching Pursuit)와 K-SVD에 대해 알아보려한다.

이제 설명은 다음과 같은 최적화 식을 푼다고 가정하고 진행한다.

즉 $\beta$는 $T_0$ sparse vector 이다.

1. OMP : $y, D$가 주어졌을때 sparse vector $\beta$를 찾는다.
2. K-SVD : $y$만 주어진 상황에서 $D,\beta$를 구한다. 하지만 이 방법론이 집중하는 부분은 $D$를 구하는 것이다.

위의 두 사항을 잘 인지해놓고 있자.

OMP(Orthogonal Matching Pursuit)

sparsity를 사용하는 연구에서 OMP는 정말 많이 사용된다. K-SVD 내부에서도 사용되니 말 다했다

일단 $\min ||y - X\beta||^2_2 ~~s.t ~ |\beta|_0 \leq T_0$ 이 문제를 푸는데 있어서 $y, D$가 주어졌고 여기에서 $\beta$를 구해본다고 생각해보자.
여기에서 $y\in \mathbb{R}^n, x\in \mathbb{R}^p, X\in \mathbb{R}^{n\times p}$이다. ($n<p$)

$X\beta$가 어떤 의미인지 생각해볼 필요가 있는데, $X\beta$는 $\beta$의 각 element에 대한 X의 columns의 선형결합이다. 그러니까, 이 sparse vector $\beta$의 각 element는 해당 element에 대응되는 D의 column을 얼마나 반영해서 선형합 할거냐는 뜻이다.
즉, $\beta$의 값은 $y$와 $X$의 column이 얼마나 유사한지에 대해 결정된다.

OMP는 이러한 사실을 사용한다. (greedy, iteratively)

위 사진은 OMP의 알고리즘이다.
한줄씩 해석 해보겠다.

Step 1. : $r_0$은 현재 유사도를 비교하고자 하는 대상이다. 가장 처음에는 $r_0=y$로 초기화 시킨다. (전체 정보 이용.) 그리고 $c_0$은 이전에 update 했던 $\beta$에 대응되는 X columns를 저장한 것이다. (모든 columns에 대해 한번만 update 한다.)

Step 2-4까지는 iteration이다.
Step 2.: $r_{i-1}$과 가장 비슷한 $X$의 column을 찾아보자. -> 가장 반영을 잘하는 column을 찾기 위해 내적의 값이 가장 큰 column을 찾는다.

Step 3.: 이제 지금까지 찾았던 columns와 이번 step에 찾았던 column을 모두 포함한 columns를 기준으로 Projection matrix를 구해본다. 그리고 $r_i$는 $(I-P_i)y$로 update한다. 여기에서 $(I-P_i)$는 $P$의 projection 대상이 되는 공간의 orthogonal complement 공간으로 projection을 의미한다. 그러니까 지금까지 업데이트 했던 차원 외의 다른 차원에 대한 $y$의 정보만을 다루겠다는거다. (이전에 고려되었던 y의 정보를 빼는 것.)

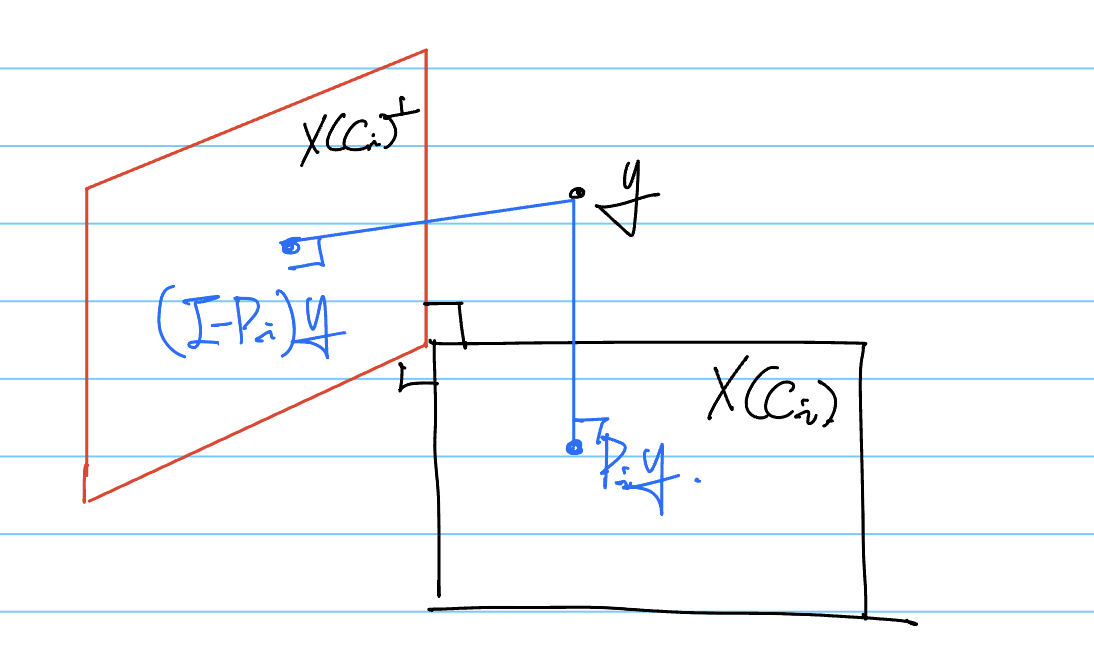
대충 이런 느낌이다.

Step 4.: Stopping condition을 확인하고 iteration을 계속 이어나가거나 중지한다. Stopping condition은 논문에서 다루고 있지만 보통 사전에 주어진 $T_0$ sparsity에 대해 iteration이 고정된다.

위의 step들을 보면 두가지 의문이 들 수 있다.
분명히 $\beta$를 update하는거라고 했는데 $\beta$는 딱히 조정을 안한다. 논문에서 잘 나타내주지 않는데, 내 생각에는 전체 iterations를 모두 거치고 적절한 columns의 indices가 구해졌을때 진행되지 않나 싶다. -> Projection matrix에서 가장 앞의 $X(c)$를 뺀 $(X(c)^TX(c))^{-1}X(c)^Ty$가 의미하는게 이 column space에 대응되는 $y'$를 내놓는 $\beta$를 구하는 것이니까. 여기에서 $c$에 포함되지 않는 columns에 대응되는 $\beta$의 elements는 0으로 두고..

두번째 의문은 step 2.에서 단순히 내적의 max를 취하는 경우 이전에 선택된 columns과 중복된 column이 선택될 수 있지 않는가에 대한 의문이다. 논문에서 말했듯이 Greedy algorithm이라서 $c_{i-1}$에 포함되지 않는 columns만을 고려한다는 제한이 들어가야할 것 같다. -> 그냥 생략해서 쓴듯?

근데 위의 알고리즘을 보면 알 수 있겠지만 Projection matrix를 계산하는 것 자체가 비교적 계산 복잡도를 증가시킨다. 챗지피티씨한테 질문해본 결과 좀 더 간단한 방법으로 구현되는 것 같다.

import numpy as np

def omp(A, y, k):
   n, d = A.shape
   x = np.zeros(d)  # 근사할 신호의 초기화
   
   for _ in range(k):
       residual = y - np.dot(A, x)  # 잔여 계산
       max_index = np.argmax(np.abs(np.dot(A.T, residual)))  # 가장 큰 기저 함수 선택
       selected_atom = A[:, max_index]
       
       x[max_index] += np.dot(selected_atom, residual)  # 선택한 기저 함수의 계수 업데이트
   
   return x

# 예제 데이터 생성
n = 100  # 신호의 길이
d = 200  # 기저 함수의 수
k = 5   # 선택할 기저 함수의 수

# 임의의 기저와 신호 생성
A = np.random.randn(n, d)
x_true = np.zeros(d)
x_true[:k] = np.random.randn(k)
y = np.dot(A, x_true)

# OMP 알고리즘 적용
x_approx = omp(A, y, k)
print("True x:", x_true)
print("Approximated x:", x_approx)

K-SVD는 다음 포스트에 기술하겠당