Manifold?

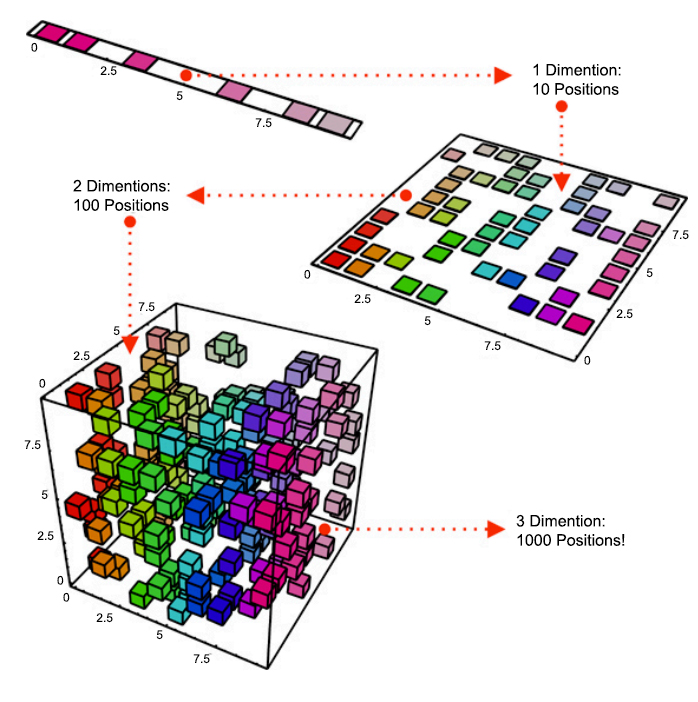http://www.infme.com/curse-of-dimensionality-ml-big-data-ml-optimization-pca/

보통 현실 세계의 데이터(Image, Text, ...)들은 더 낮은 dimension으로 표현이 가능하다. 예를들어 (32 x 32 x 3)의 이미지가 있다고 해보자. 이 이미지는 8bit로, 0~255 닫힌 구간의 이산값을 갖을 수 있다.

이런 경우 32 x 32 x 3 모두에 대해 256개의 값을 갖을 수 있기 때문에 총 경우의 수는 $256^{32 \times 32 \times 3}$이 된다.
예시로 들었던 해당 이미지에 대한 분포에 대한 경우의 수보다 훨씬 더 큰 수이다. $256^{32 \times 32 \times 3}$는 생각보다 너무나도 큰 수이다.

위의 한 단락의 내용을 간단히 말하자면, 우리가 평소에 다루는 데이터는 데이터로 표현되는 차원보다 더 낮은 차원으로 표현할 수 있다는 것이다.

Sparse?

보통 어떤 정보를 데이터로 다루기 위해서 sampling(time, spatial domain에서의 이산화), quantization(value에 대한 이산화)을 거치게 되고 이는 vector(array, list, ...)로 표현될 수 있다.
Sparse vector는 이 vector를 이루는 값이 대부분 0으로 이루어져 있다는 것이다.
수학적으로 s-sparse를 0이 아닌 값의 성분이 s개 이하인 것으로 정의하고 이는 대부분의 값이 0으로 이루어져 있음을 의미한다.

간단하게 수식적으로 적어보자. support를 사용하여 정의한다. (수식적으로 깊이 이해하려는게 아니면 굳이 알 필요 없다.)

$supp$이 의미하는 바는 vector x에서 값이 0이 아닌 성분의 indices set을 의미하고 $card$는 set의 크기 (cardinality)를 의미한다.
$s$를 사용자가 설정한 작은 값이라고 생각하면, 결국 s-sparse는 대부분의 값이 0으로 이루어진 sparse vector임을 의미한다.

여기에서 이렇게 sparsity에 대한 이야기를 하는 이유는, 위에서 언급했듯 우리고 평소에 다루는 데이터는 데이터로 표현되는 차원보다 더 낮은 차원으로 표현 될 수 있고, 즉 이는 동일 차원에서 sparse한 형태로 나타낼 수 있음을 의미한다.

선형대수를 통해 나 나름대로 직관적으로 해석해보겠다 (SVD, Singular Value Decomposition)

어떤 $A\in \mathbb{R^{m\times n}}$가 있다고 가정해보자 (Dataset). $A=U\Sigma V^T$ 이런식으로 SVD를 통해 표현될 수 있다. 근데 A가 데이터료 표현되는 차원보다 더 낮은 차원으로 표현될 수 있다는 것은 이 Dataset이 상주하는 Space에 대한 Basis의 개수가 $\min (m,n)$보다 작다는 뜻이고, 즉 Singular value matrix $\Sigma$는 우측 하단 block이 0으로 이루어짐을 알 수 있다.

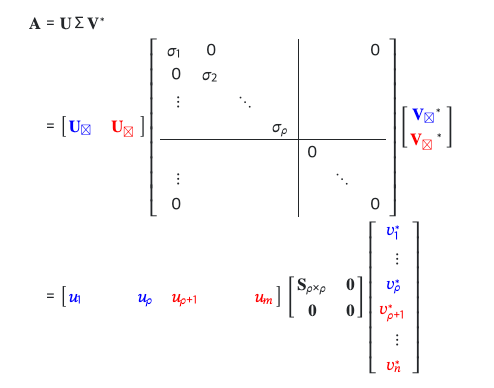https://math.stackexchange.com/questions/1771013/how-is-the-null-space-related-to-singular-value-decomposition

이 그림처럼 말이다.

이는 결국 동일 차원에서 해당 데이터를 표현할 때 sparse하게 표현할 수 있음을 보여준다.
즉 선형대수학 관점에서 Sparse data가 존재함을 확인했다. ㅎ.ㅎ

$V$ matrix에서 zero singular values와 대응되는 vector들은 A의 Null space $N(A)$의 Orthonormal Bases이다. : https://pillowlab.princeton.edu/teaching/statneuro2018/slides/notes03a_SVDandLinSys.pdf (Vector space에 대한 linearity 때문.)
이런 Null space에 대한 언급을 한 이유는, 결국 Sparse함은 Null Space와 관련이 있다는 것을 말하고 싶어서이다. (사실 현재 맥락에서 맞지는 않지만..)
머신러닝이나 딥러닝 관련하여 공부나 연구를 하다보면 언젠가는 Null Space와 Column Space에 대한 고려를 하게 된다. (Optimization Problem에서의 Dual Form이라던지, non invertible한 ill-posed problem에 대한 고려라던지..)
현재 포스트를 포함한 이후의 포스트들에서 이러한 사항에 있어서 관련이 있다면 계속 언급하여 익숙해지고 직관을 얻고자 한다. (독자도 이와 같이 뜬금없이 언급된 사항에 대해 고민하는 시간을 갖으면 좋을 것 같다.)

Examples

직접적인 연관 예시는 아니지만 Data Compression 관점에서의 인접한 예시 하나를 들어보자.

Data Driven Science & Engineering.pdf Ch3

어떤 이미지가 주어졌을때 Fourier Transform과 shift operation을 거쳐 magnitude를 시각화 하면 위 Figure의 우측 상단처럼 나온다. 보면 high quality(이미지의 가장자리)에 대한 coefficient가 존재함을 알 수 있다.
근데 이 Fourier Coefficient에서 거의 Low frequency information만을 남겨놓고 (5%, Sparse Vector) 모두 삭제한 후 inverse fourier transform을 거치면 시각적으로 차이가 거의 없는 이미지가 나온다.
즉, 비슷한 이미지를 Sparse하게 표현할 수 있다는 것이다.

Compressed Sensing

이제 이러한 Sparse 성질을 잘 활용할 수 있는 부분에 대해 설명하려고 한다. 우리는 어떤 signal을 받았을때 이를 그대로 사용할 수 없고 결국 샘플링 과정을 거쳐야한다. 이 샘플링을 실행할 때에 까다로운 Rule을 하나 지켜야하는데, 이를 Shannon Nyquist Sampling Theorem이라고 한다. 간단하게 설명하면 샘플링된 데이터를 완전히 복원하기 위해서는, 데이터로 사용하고자 하는 signal의 최대 주파수의 2배 이상의 sampling rate로 샘플링 해야한다는 것이다.
근데 sparsity를 통해서 이러한 Rule을 크게 극복할 수 있다. 이러한 sampling 과정을 합쳐서 수식적으로 우선 표현해보자.

($x$는 data, $\Phi$는 Sparse한 값으로 만드는 Space의 Basis, $s$는 Sparse Vector, $C$는 Sampling matrix, $y$는 Sampling된 data)

여기에서 대표적인 $\Phi$는 Fourier Basis이다.

일단 주어진 data $x$에서 샘플링을 수행할 때 기존의 sampling처럼 일정한 timestep을 두고 regular하게 샘플링을 진행하는게 아니라 전체 data $x$ 중에서 1/32 정도만 랜덤샘플링을 해보자.

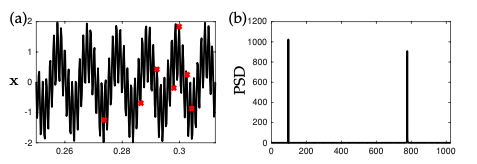Data Driven Science & Engineering.pdf Ch3

그럼 위처럼 수행되게 된다.
위에서 정의했던 식 그대로 적용을 할 수 있다. $y=C\Phi s$에서 $y, C, \Phi$를 알고 있는 상황이고, 이대로 풀기 보다는 $s$가 sparse vector임을 보장해야하기 때문에 변수 선택의 효과를 볼 수 있는 L1 Regularization과 같은 Penalty Term을 추가하여 Optimization problem을 풀 수 있다. (위의 책에서는 COSAMP를 사용한다.)

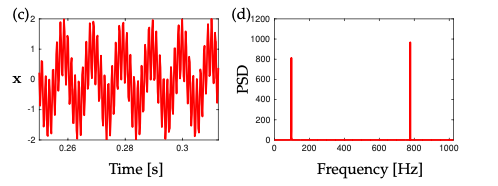Data Driven Science & Engineering.pdf Ch3

이와 같이 최적화 문제를 풀면 거의 모든 information이 복원된다.

이는 Random Sampling과 같이 $\Phi$와 incoherence 혹은 무관한 Sampling Matrix를 사용 시, Shannon Nyquist Sampling Theorem에서 요구하는 sampling frequency보다 훨씬 더 적은 sample 만으로도 완전한 복구가 가능할 확률이 높다는 것을 의미한다.

위의 조건과 measurement 수에 대한 어떤 조건이 만족되면 Restricted Isometric Property를 만족하게 되어 해당 문제를 풀 확률이 90% 이상이라는 것이 증명되었다. (증명된 사항.)
the number of measurement $\approx K_1O(k\log(n/k))$
$K_1$은 incoherence와 관련된 constant라고 보면 되고, $n$은 원래 measurement의 수이며 $k$ 는 k-sparsity를 의미한다.

근데 잘 생각해보면 수식이 다소 까다롭다. 이게 무슨말이냐면 $\Phi, C$를 모두 알아야 풀 수 있는 식이기 때문에 DL/ML 분야에서 사용하기가 쉽지 않다. 그래서 오래된 논문부터 최근 논문까지도 $\Phi, s$를 훈련하여 찾는 방법들이 많이 연구된다. (K-SVD, OMP, MP, ...)

이와 같이 유연하게 사용될 수 있다면 무궁무진하게 적용이 가능하지 않을까 생각한다.