CVPR 2024 best student paper로 선정된 Mip-Splatting을 읽고 요약하였다.

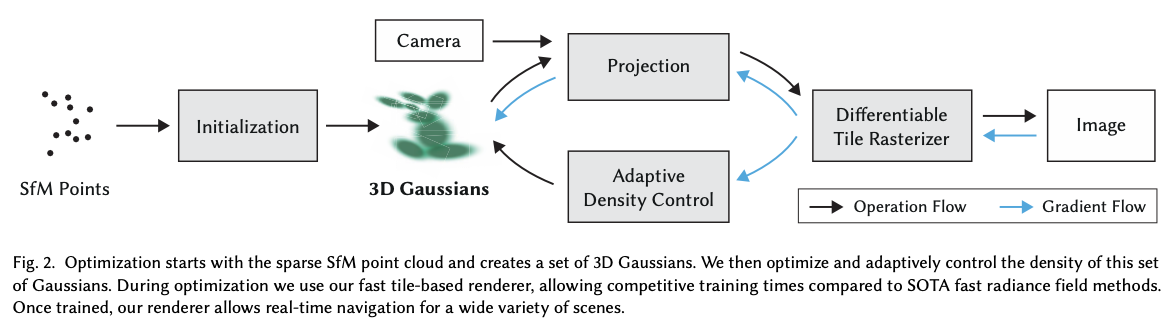
3D gaussian splatting

3D Gaussian Splatting for Real-Time Radiance Field Rendering

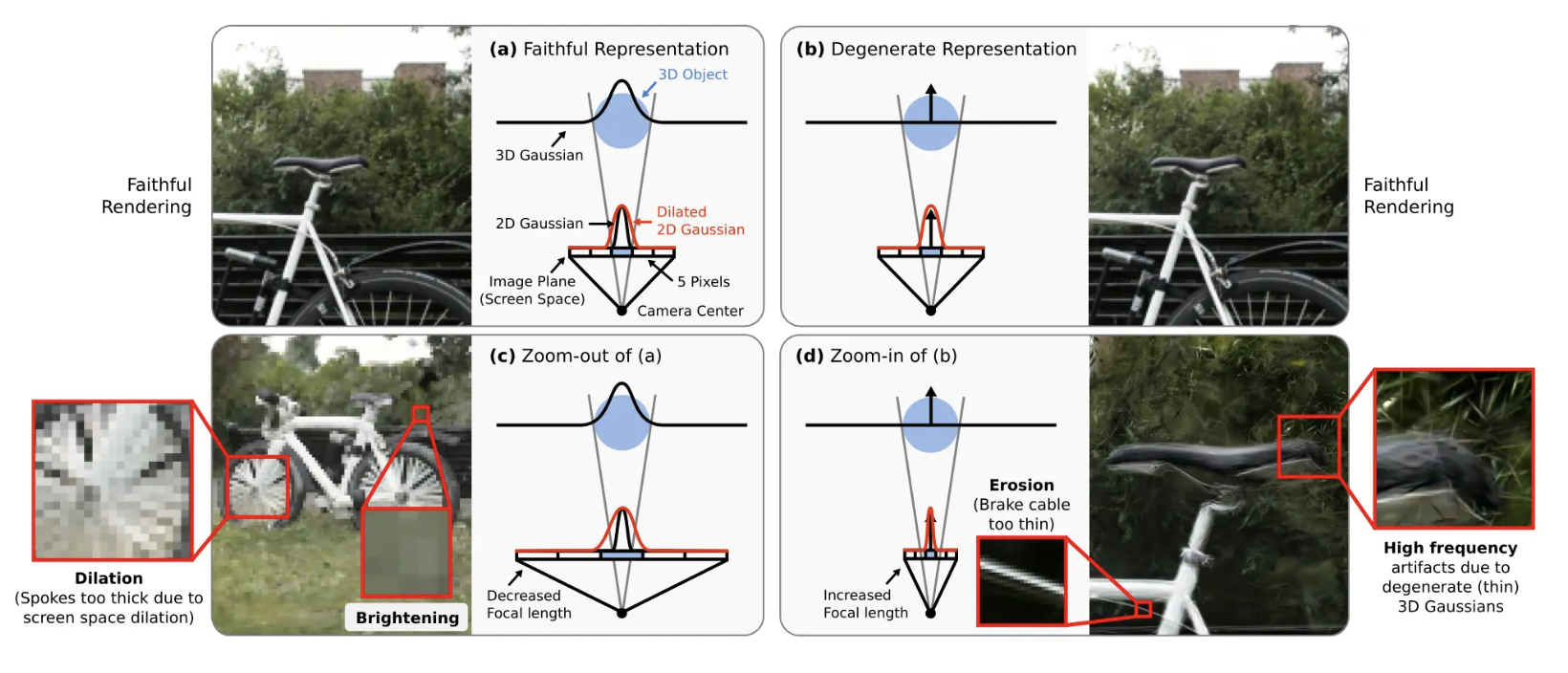
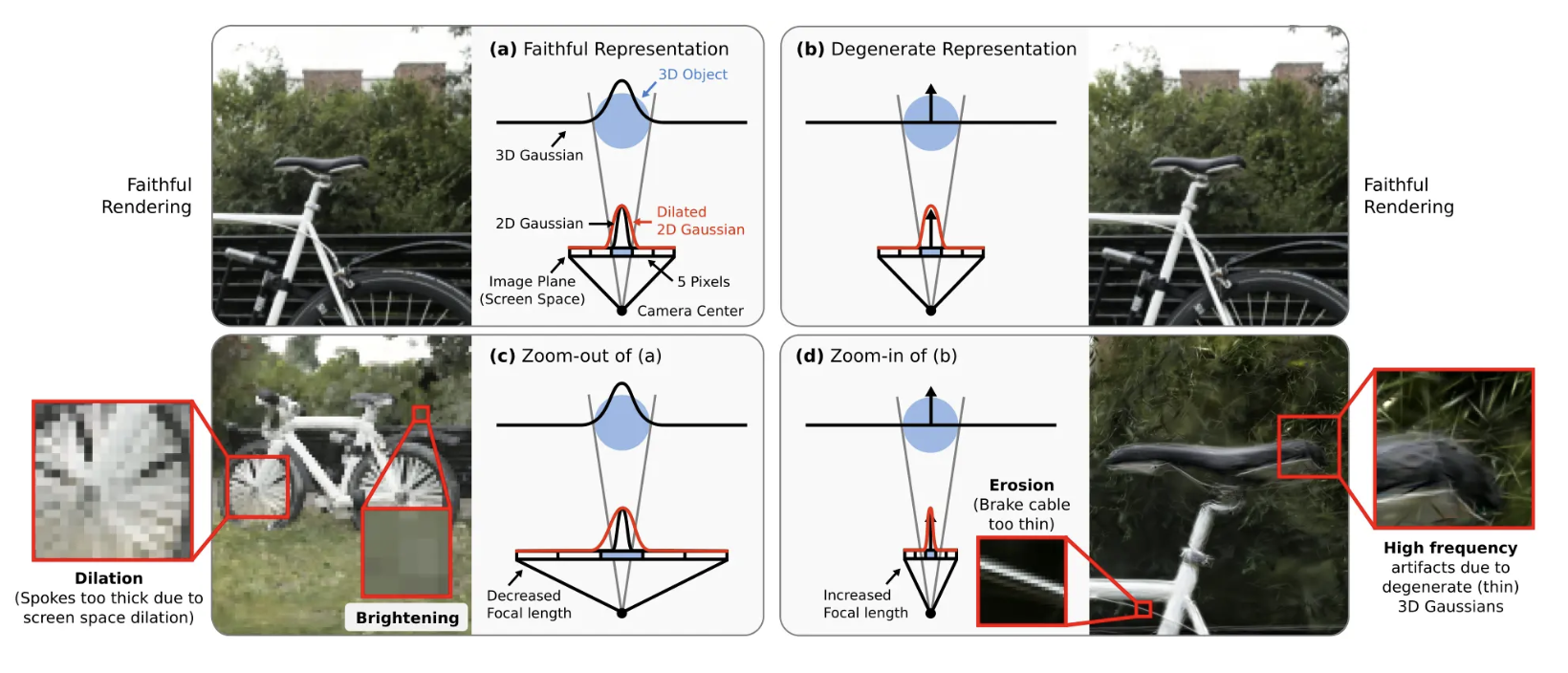
원본 가우시안 스플래팅에 3D smoothing filter를 추가해 줌인했을 때의 high freq artifacts를 제거하였다.

Mip-Splatting은 원본 3DGS에서 사용하는 low pass filter (2D screen space dilation filter)를 2D Mip filter로 대체하여 aliasing/dilation 문제를 해소하였다.

Mip Splatting

3D smoothing filter

나이퀴스트 이론을 적용한다.

• sampling rate가 입력신호의 최대 주파수의 2배 이상은 되어야 연속신호를 디지털화한 후 최대한 손실 없이 복원할 수 있다는 이론...이라고 알고 있다. 자세한 건 이 블로그 포스트를 참고하면 좋을 것 같다.

훈련 과정에서 Representation의 최대 주파수가 sampling rate의 반 이하가 되도록 한다. 간단하게 표현하면

• $(\text{max rep freq}) \leq (\text{half the sampling rate}) = \frac{f}{2d}$

• 한 가우시안의 최대 sampling rate $\hat{v}_k = max(\{ \text{view frustum 내 존재 여부} \ \cdot \ \frac{f_n}{d_n}\}^N _{n=1})$

• 즉, $\frac{f}{2d} \geq \hat{v}_k$가 성립하도록 representation의 frequency를 통제한다.

이 과정을 아래 이미지에서 확인할 수 있다. 이 과정은 즉 2D로 project했을 때 최소 하나의 픽셀에 대응할 수 있도록 world space의 주기 $\hat{T}$을 결정하는 것이다. $\hat{v}_k$는 매 100 iter마다 다시 계산한다.

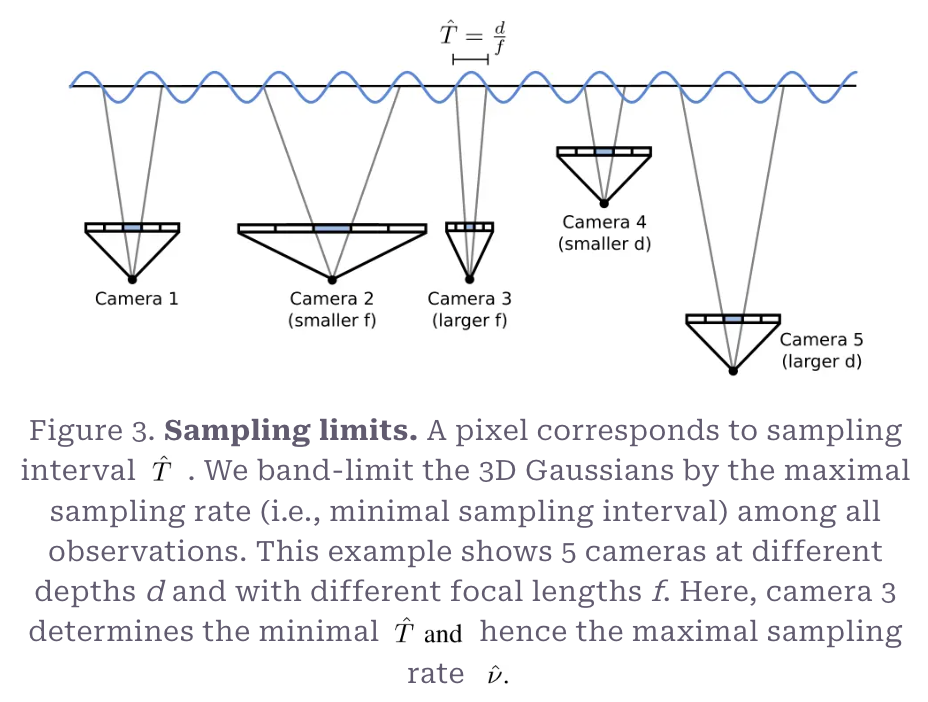
$\hat{v}_k$를 구했으면 이를 실제로 representation에 적용해야 한다. 이는 아래 식으로 정리된다.

• $\mathcal{G}_k(\bold{x})_{reg} = (\mathcal{G}_k \otimes \mathcal{G}_{low})(\bold{x})$
  • $\mathcal{G}_k(\bold{x})_{reg} = \sqrt{\frac{|\sum_k|}{|\sum_k + \frac{s}{\hat{v}_k} \cdot \bold{I}|}} e^{-\frac{1}{2}(\bold{x}-\bold{p_k})^T(\bold{\sum}_k+\frac{s}{\hat{v}_k} \cdot \bold{I})^{-1}(\bold{x}-\bold{p_k})}$
  • 각각 $\sum_1$, $\sum_2$를 covariance matrix로 가진 가우시안 두 개를 연산했을 때 $\sum_1 + \sum_2$를 convariance matrix로 가진 가우시안을 결과로 하므로 효율적이다.
    $s$: filter size hyperparameter

이렇게 계산한 $\mathcal{G}_{low}$는 테스트 시에는 조정되지 않고 각 가우시안의 intrinsic과 같은 역할을 한다. 실험에서 s=0.2로 설정하였다.

3D Smoothing filter가 적용되는 부분 코드

2D Mip filter

$\mathcal{G}_k^{2D}(\bold{x}) = e^{-\frac{1}{2}(\bold{x}-\bold{p_k})^T(\bold{\sum}_k^{2D}+s \bold{I})^{-1}(\bold{x}-\bold{p_k})}$,
$s$: dilation hyperparameter

위 식은 Mip에서 제시하는 원본 3DGS의 2D 가우시안 식이다. 가우시안이 픽셀 크기보다 작을 때 최소 픽셀 크기가 되도록 크기를 키워준다. (= '2D screen space dilation') 이는 아래 사진의 (b)에서 확인할 수 있다.

원본 가우시안 스플래팅 코드에서 low-pass filter를 적용하는 부분을 확인할 수 있다. 이때 아래 사진에서도 볼 수 있듯 원본 가우시안 스플래팅에서는 s=0.3으로 설정하였다.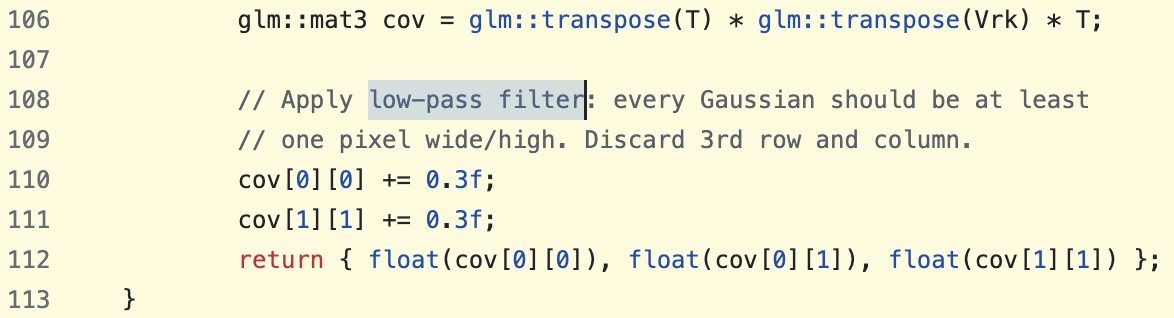

2D Mip filter는 안티앨리어싱을 수행한다는 데에 있어 EWA splatting과 비슷하지만, EWA보다 줌아웃 했을 때의 artifacts/dilation과 oversmoothing 현상이 덜하다. EWA는 필터 크기를 휴리스틱하게 정하는 반면 Mip filter는 인풋의 픽셀 크기로부터 결정된다. EWA는 단위행렬 covariance matrix를 사용해 3x3 픽셀 영역에 대해 나이퀴스트 이론을 반하지 않도록 제한하는데, Mip은 이런 접근방식이 oversmoothing으로 이어지는 원인이라고 지적한다. 이 외에도 Mip 필터와 EWA가 근본적으로 다르게 하는 것은 Mip은 한 픽셀의 크기에 따라 resolution을 결정하고 inverse rendering을 통해 3D Gaussian 표현을 optimize하고자 하는 반면, EWA는 전체적인 frequency bandwidth를 제한하고자 하고 렌더링에 대해서만 논의한다는 점이다.

$\mathcal{G}_k^{2D}(\bold{x})_{mip} = \sqrt{\frac{|\sum^{2D}_k|}{|\sum^{2D}_k + s\bold{I}|}}e^{-\frac{1}{2}(\bold{x}-\bold{p_k})^T(\bold{\sum}_k^{2D}+s \bold{I})^{-1}(\bold{x}-\bold{p_k})}$

위 식 (Mip)에는 원본의 2D 가우시안 식에 루트항이 추가되었다. 실험에서 s=0.1로 설정하였다.

• 관련 깃헙이슈: What does filter_size mean?

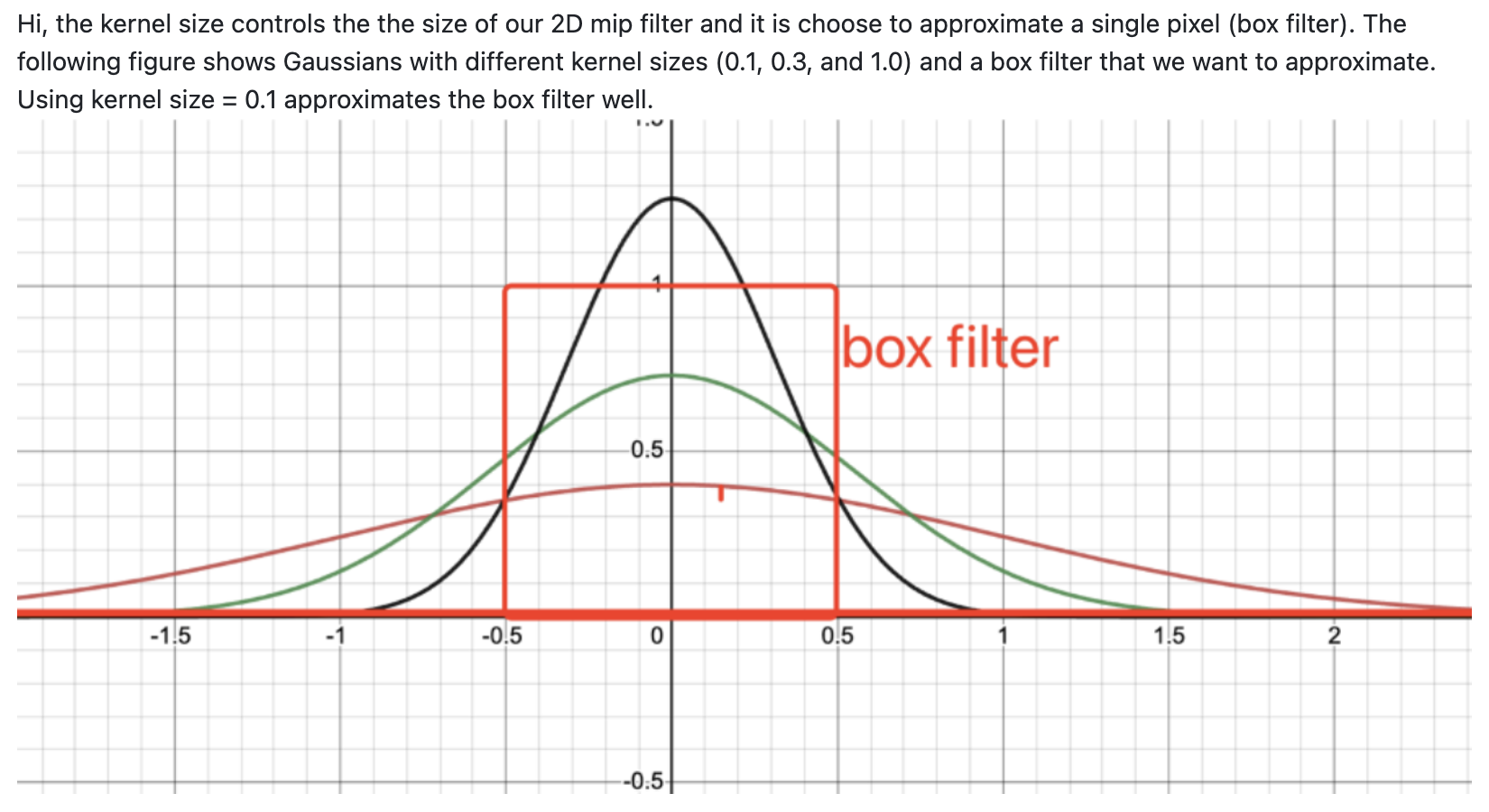
  • 커널 사이즈 ($s$)를 0.1로 설정하는 것은 가우시안이 한 개의 픽셀에 매핑이 되는 box filter (빨간색 사각형)의 크기가 되도록 하는 것이다.

2D Mip filter가 적용되는 부분 코드

• filter 내 영역을 평균내는 box filter보다 2D 가우시안 필터를 사용하는 게 더 효율적이다.
  • 2D 가우시안 필터는 두 개의 1D 가우시안 필터로 분해할 수 있기 때문 (O(n))

Experiments

다른 모델들과 비교하기 위해 줌인 & 줌아웃을 모사하였다.

• Zoom in (Higher res): Downsampled 데이터에 비교군들을 새로 훈련 후 higher resolution으로 렌더링
• Zoom out (Lower res): Full resolution으로 비교군들을 새로 훈련 후 1x, 1/2, 1/4, 1/8의 focal length로 조정해 여러 resolution으로 렌더링

위 사진에서 다양한 스케일로의 줌아웃을 모사한 테스트 데이터 샘플을 볼 수 있다.

Trained on multi-scale + Tested on mutli-scale

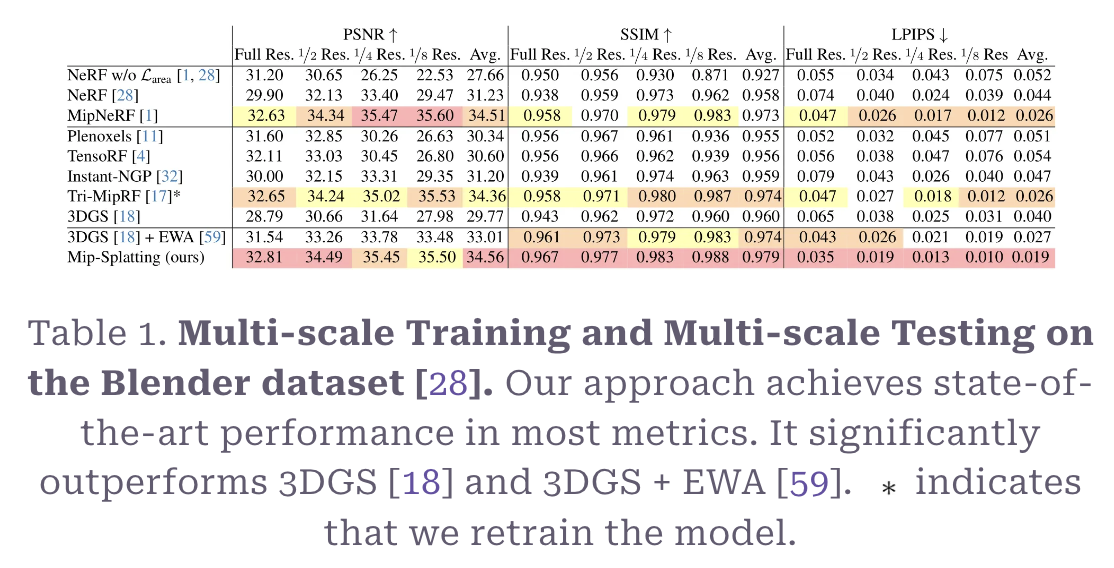
위 표는 줌아웃 시나리오에서의 메트릭 비교이다. 원본과의 해상도, 구조적으로 비슷한 정도와 딥러닝 모델에서 인지하는 방식의 차이에서 다른 모델에 비해 대부분 좋은 성능을 보였다.

Trained on a single scale + Tested on multi-scale

타 모델과의 비교

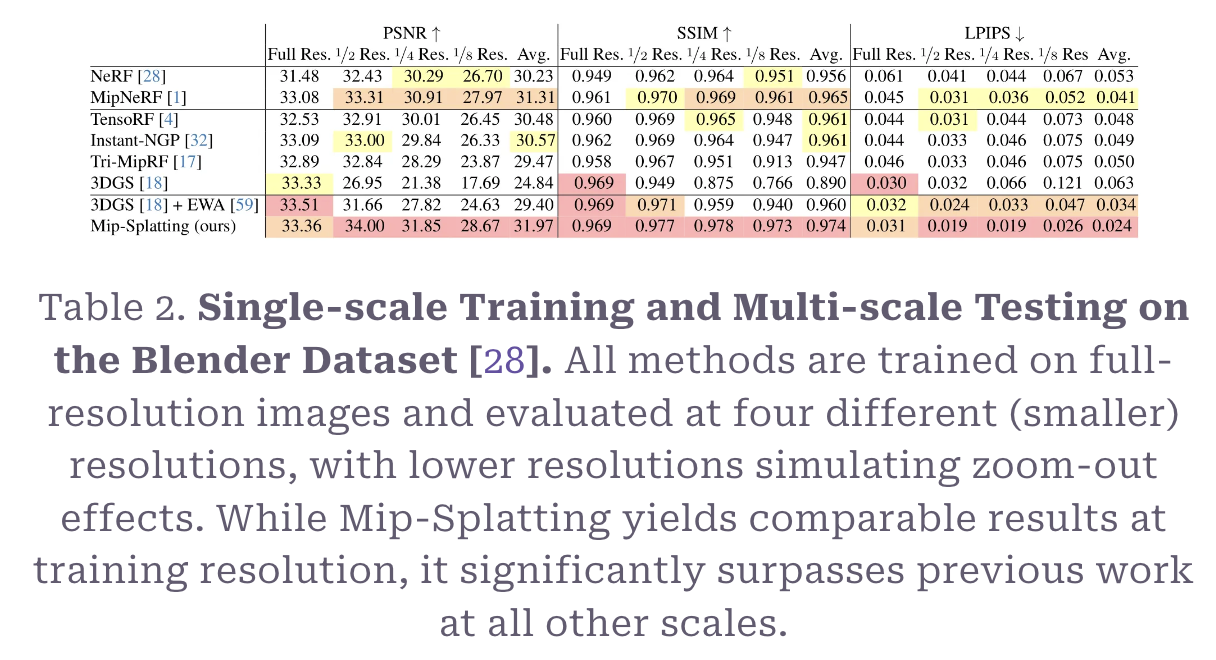
위 표는 줌아웃 시나리오에서 Mip과 타 모델의 메트릭이다. 대부분의 메트릭에서 Mip의 성능이 좋게 나왔음을 알 수 있다.

위 사진은 줌인과 줌아웃을 모사한 모델들과 Mip의 렌더링된 사진들이다. Artifact가 많은 다른 모델들에 비해 Mip이 여러 해상도에서 더 나은 결과를 보였다.

제시된 너프 기반 모델들보다 3DGS 기반 모델이 원본 해상도에서 디테일을 더 잘 잡는다고 한다. 낮은 해상도에서는 Mip이 원본 3DGS와 3DGS에 EWA를 적용한 것보다 성능이 뛰어나다.

위 그림은 줌인했을 때의 결과인데, 다른 모델보다 Mip에서 high frequency artifacts가 덜하다.

어블레이션

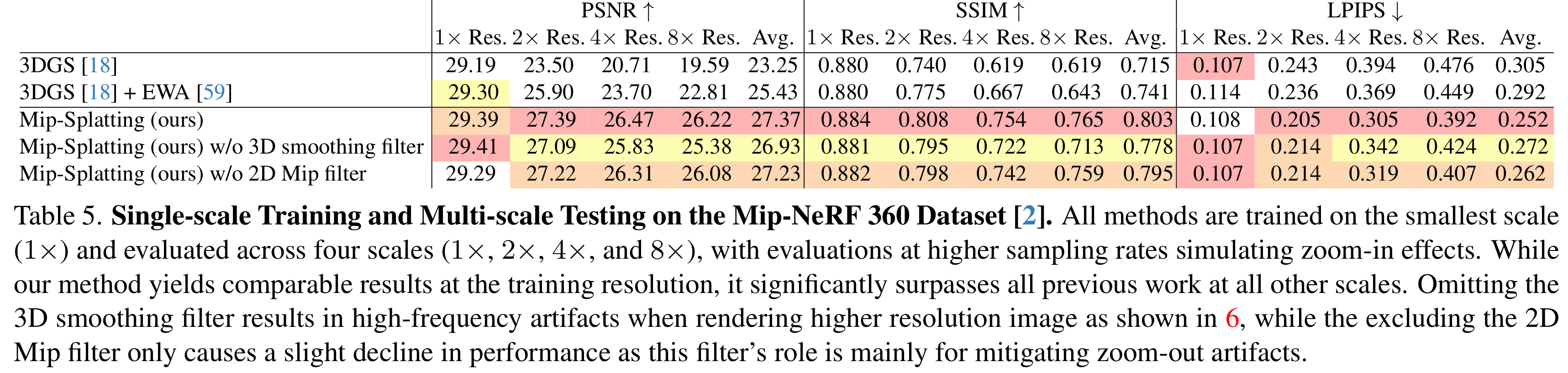
위 표는 Mip-NeRF 데이터셋을 사용해 수행한 줌인 시나리오에서의 Mip필터와 3D smoothing 필터에 대한 어블레이션 실험 결과이다. 3D smoothing filter를 사용하지 않으면 줌인 시의 성능이 떨어지는 것을 볼 수 있다.

위 그림은 줌인 시나리오에서의 어블레이션 퀄리티 결과이다. 육안으로 봤을 때 확실히 3D smoothing filter가 줌인 시의 아티팩트를 크게 줄여주고, 2D Mip filter가 조금 더 선명하게 하는 효과가 있는 것 같다.

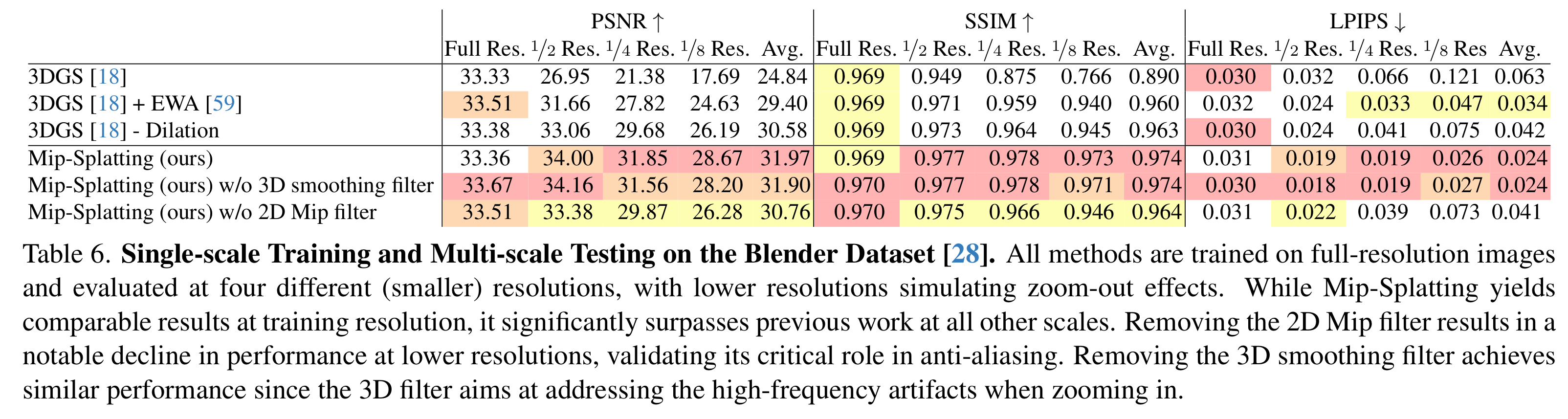
위 표는 블렌더 데이터셋에서 수행한 어블레이션 실험인데, 줌아웃 했을 때 2D Mip filter를 사용하지 않으면 성능이 떨어진다.

위 그림은 줌인과 줌아웃 시 타 모델 비교 & 어블레이션에 대한 퀄리티 결과이다.

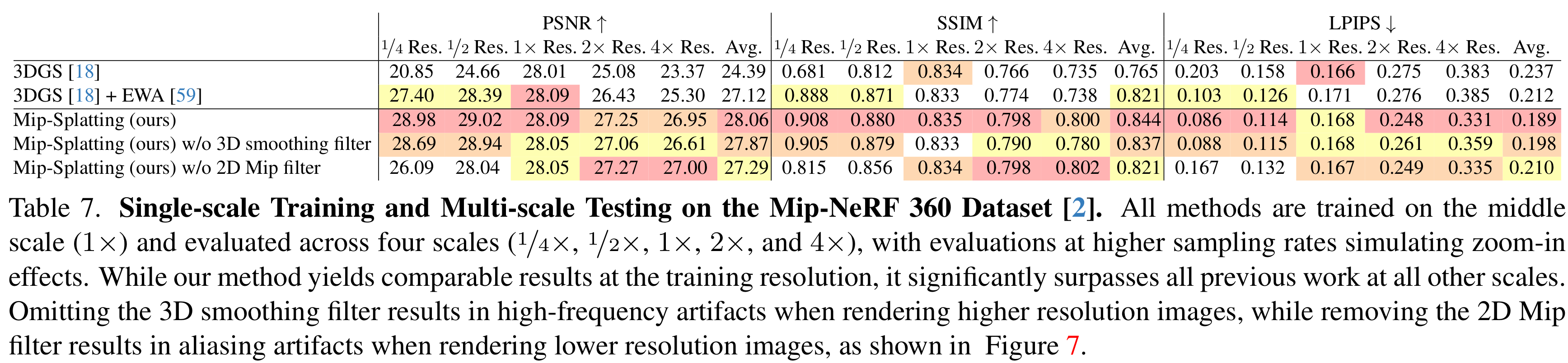
줌인했을 때와 줌아웃했을 때의 어블레이션이다. 줌인했을 때 2D Mip filter를 쓰지 않으면 성능이 더 좋은 경우가 있어 보인다.

Trained and tested on the same scale

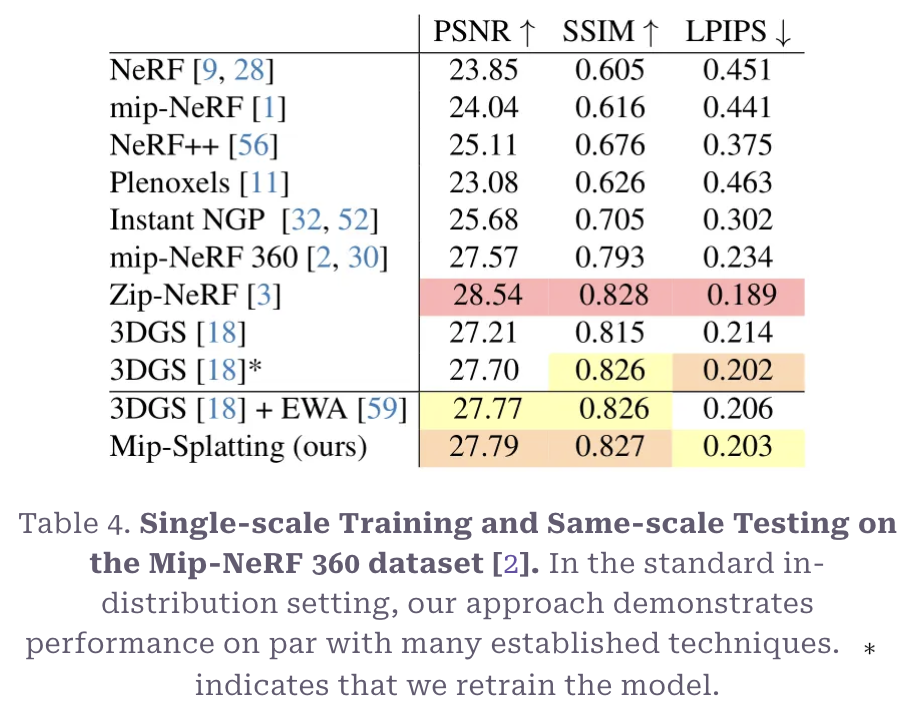
위 표를 봤을 때 Zip-NeRF가 가장 좋은 성능을 보이긴 하나 3DGS나 3DGS+EWA와 비교했을 때 떨어지는 성능을 보이진 않는다.

틀린 부분 지적이나 관련 내용에 대한 댓글 환영합니다. 감사합니다.