Total-Decom: Decomposed 3D Scene Reconstruction with Minimal Interaction

| Paper arXiv | Introduction to Total-Decom | Github repo |

Decomposition is the key to manipulate and edit the 3D geometry of the reconstructed scene.

Neural implicit feature distillation

Normal

• gradient of SDF: the direction of the surface normal
• $\text{Normal}(p) = \frac{\nabla d(p)}{|\nabla d(p)|}$

Depth

• directly obtained from the SDF values along the ray
• $\text{Depth}(p) = \int_{t_{near}}^{t_{far}} T(t) \sigma(t) t , dt$

Semantic Logits

• class probabilities for semantic segmentation at each sample point
• features extracted from the SAM encoder
• $\text{Semantic Logits}(p) = \int_{t_{near}}^{t_{far}} T(t) \sigma(t) \text{logits}(t) , dt$

Generalized Features

• texture, material properties, ...
• $\text{Generalized Features}(p) = \int_{t_{near}}^{t_{far}} T(t) \sigma(t) \text{features}(t) , dt$

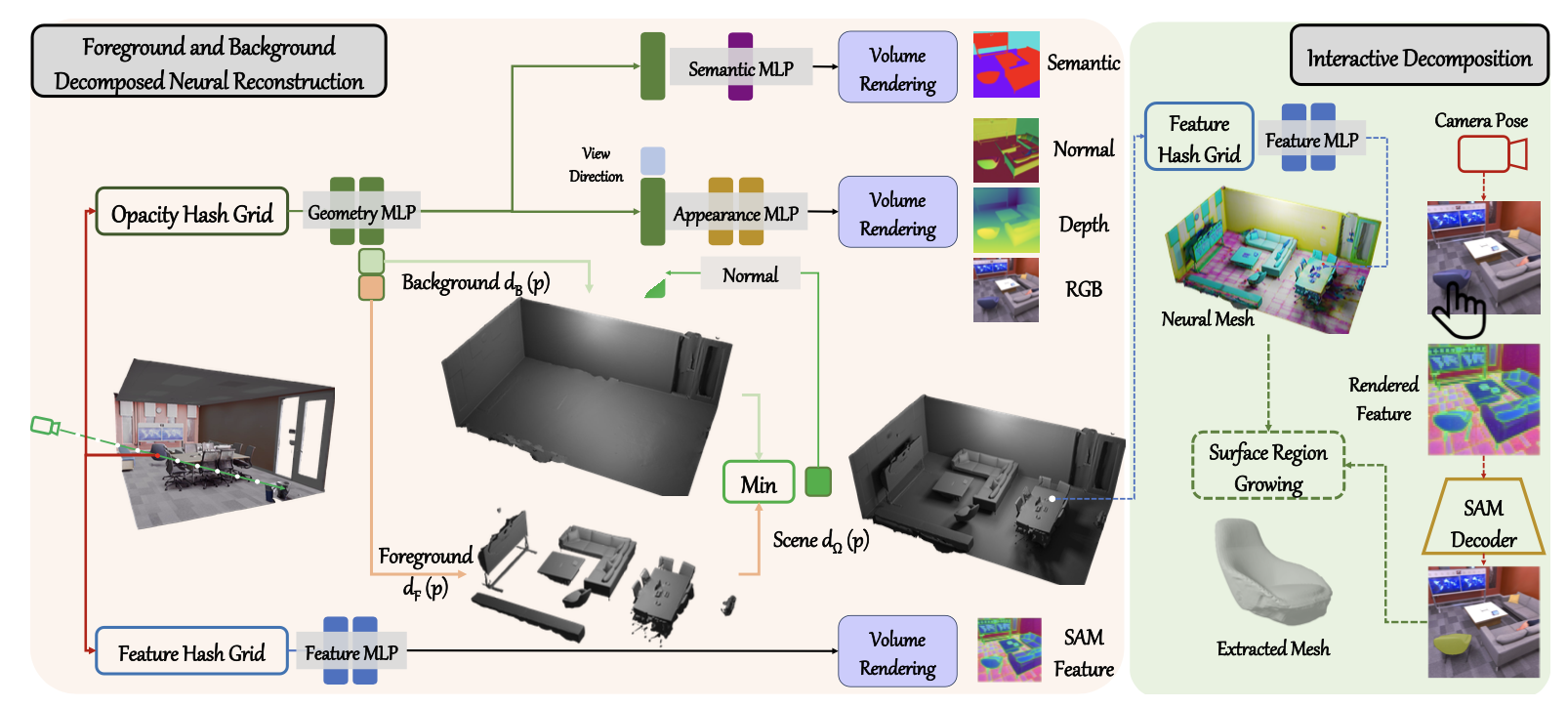
Foreground and Background Decomposed Neural Reconstruction

Foreground

: Objects

• 각 Foreground와 Background는 SDF field를 따로 가짐
  • $\mathcal{S} = \{\mathcal{F, B}\}$, 최종 scene은 $\Omega = \mathcal{F} \cup \mathcal{B}$, 최종 scene SDF는 두 SDF의 $min$
  • SDF function $d(p)$, point $p$
  • ray $r(t) = o + tv$ Camera position $o$, direction $v$
  • Color $C(p, v)$, SDF $S(p)$, generalized feature $F(p)$
• Occlusion-aware Opacity Rendering: Guides the learning process $\rarr \mathcal{L}_{O}$
• Object Distinction Regularization: Ensures a clean foreground mesh $\rarr \mathcal{L}_{reg}$

Background

: Walls, floors, ceilings

• Manhattan World Assumption: 인공 구조물은 x, y, z축을 따라 만들어졌다는 가정 $\rarr \mathcal{L}_{man}$
• Root Finding Method: 천장에서 ray를 쏘아 surface에 부딪치면 floor로 가정 $\rarr \mathcal{L}_{floor}$
  • Root는 SDF=0, 즉 $d(p + t \cdot \mathbf{d}) = 0$ 임

Loss function

$\mathcal{L} = \mathcal{L}_{rgb} + \mathcal{L}_{geo} + \lambda_1 \mathcal{L}_O + λ_2\mathcal{L}_{reg} + λ_3\mathcal{L}_{man} + λ_4\mathcal{L}_{floor} + λ_5\mathcal{L}_{sem} + λ_6\mathcal{L}_f$

• $\mathcal{L}_{rgb}, \mathcal{L}_{geo}$ : MonoSDF
• $\mathcal{L}_O = \mathbb{E}_{r∈\mathcal{R}}[\sum_{S_i \in S}||\hat{O}_{S_i}(r)−O_{S_i}(r) ||]$
• $\mathcal{L}_{reg} = \mathbb{E}_p[\sum_{d_{S_i}(p) \not = d_\Omega(p)} \text{ReLU}(-d_{S _i}(p)-d_\Omega (p))]$
• $\mathcal{L}_{man} = \mathbb{E}_{r \in \mathfrak{F}}(\hat{p}_f (r)|1-\hat{n} (r) . n_f |) + \mathbb{E}_{r \in \mathfrak{W}} (min_{i \in \{-1, 0, 1\}} \hat{p}_w (r) |i - \hat{n}(r) . n_w|)$
  • $\hat{p}_f, \hat{p}_w$ : prob of the pixel being floor and wall (from semantic MLP)
  • $\mathfrak{F, W}$ : sets of camera rays of the pixels labeled as floors and walls
  • $\hat{n}_r$ : rendering normal of rays $r$
  • $n_f = <0, 0, 1>$
• $\mathcal{L}_{floor} = |1-n(p_f) . n_f|$
  • $p_f, n_f$ : floor, the assumed normal direction in the floor regions
  • $n_w$ : learnable normal for walls
• $L_{sem} = −\mathbb{E}_{r∈\mathcal{R}}[\sum ^L _{l=1}P_l(r)log\hat{P}_l(r)]$
  • Cross-entropy loss
  • $P_l(r), \hat{P}_l(r)$ : multi-class semantic probability as class $l$ of the ground truth map and rendering map for ray $r$
• $\mathcal{L}_f$ : L2 loss, rendered generalized feature $\hat{F}(r)$ for distilling the $F(r)$ from the SAM encoder
• $\lambda$ = 0.1, 0.1, 0.01, 0.01, 0.5, 0.1

Interactive decomposition

• Mesh Surface Extraction: Converting implicit neural representations into explicit mesh representations

• Feature Distillation: Features into mesh vertices

• Object Seeds Generation: SAM features and human clicks to generate initial object seeds

• Region-growing Algorithm

  • foreground mesh를 얻어 이에만 growing 알고리즘을 적용함으로써 low-noise에서의 growth 가능
  • 각 object에 속하는 seed가 object 전체를 덮도록 확장되어 segmentation을 더 잘 하도록 도움

Object Decomposition

• Seed Points Expansion: Initial seed points expanded along the mesh using a region-growing method
  • $sim(f_s, f_n) <- \frac{f_s . f_n}{||f_s|| ||f_n||}$
  • Boundary Constraints
    • 2D seed pixels and boundary pixels are references for 3D seed vertices and boundary vertices
    • SAM decoder: provides dense mask
    • explicit geometry information (vertices and edges): rules out vertices with high feature similarities

Evaluation

• Replica and ScanNet
• Metrics: Acc, Comp, C-L1, Prec, Recall, F-score