Setup Machine Learning Application

Datasets

데이터셋 종류

• Train set
• Dev set (Hold-out cross validation set)
• Test set

결국 반복해야 한다.

• Idea, code, experiment
• 트레인 셋으로 학습하고, 데브 셋에 맞게 모델을 수정하고, 테스트 셋으로 평가한다.
• 완벽한 세팅을 한 번에 할 수 없으니 반복하면서 경험적으로 모델을 완성한다.

데이터 분할

• 데이터 총량 따라서 Train/Dev/Test set을 알아서 분할하면 된다.
• 60%/20%/20%해도 되고, 데이터가 엄청많다면 99.5%/0.25%/0.25% 해도 된다.

데브셋 분포

• dev, test set의 분포는 동일해야 한다.
  • dev set은 4K고화질의 깔끔한 사진인데, test set이 32 x 32px짜리 이상한 사진이면 안된다. 둘이 비슷해야 한다.
• 크롤링 등으로 무작위에 가까운 대량데이터를 수집하면 이 법칙이 깨지기 쉽다.
  • 그러나 dev, test set의 분포가 동일해야 한다는 대전제를 항상 마음에 품을 것
  • 그러면 idea, code, experiment의 이터레이션이 빠르게 진행될 수 있을 것.

Dev set이 없는 경우.

• Train/Test set으로만 분할하는 경우, test set으로 평가하고 모델을 조정하게 된다.
• 이거 이름만 test set이지 사실 하는일은 dev set이다.
• 이렇게 2개 세트로 구분된 경우 overfitting될 수 있다.
  • 그러나 unbiased estimation이 필요하지 않은 경우는 괜찮다.

Bias(편향) / Variance(분산)

군대 영점사격지로 보는 편향과 분산

high bias

• 모델이 너무 단순해서 복잡한 패턴 학습 못하는 경우.
• Underfitting
• 해결책 : 더 큰 네트워크 사용, 훈련시간 증가, 더 좋은 NN 아키텍쳐 사용

High variance

• 모델이 너무 복잡해서 train set에만 성능이 좋고, 새로운 데이터 예측은 잘 못하는 경우
• Overfitting
• 해결책 : 더 많은 데이터 확보. 데이터 정규화(Regularization)

Trade-off

• bias를 낮추면 variance가 오르고, variance를 낮추면 bias가 오를 수 있다.
• 적당한 그 사이의 최적지점을 찾아야 된다.

데이터셋의 오류 정도로 상태 진단해보기

• 가정
  • 사람은 딱보면 잘 아는 데이터셋임.
  • Bayes오류가 작고, train,dev set이 동일한 분포에서 추출됨.
• High bias
  • train, dev set 둘 다 오류 비슷한 정도로 높다.
  • Underfitting
• High variance
  • train set 오류 낮다 / dev set 오류 높다.
  • Overfitting.
• High bias + variance
  • train, dev set 둘 다 오류 높다. (dev set 오류가 좀 더 높다. )
  • Under,Overfitting 둘 다. (영역별로 다름)
• Low bias + variance :
  • train, dev set 둘 다 오류 낮다.
  • 우리가 찾는 유니콘. 적당히 복잡한 모델.

Basic Recipe for ML

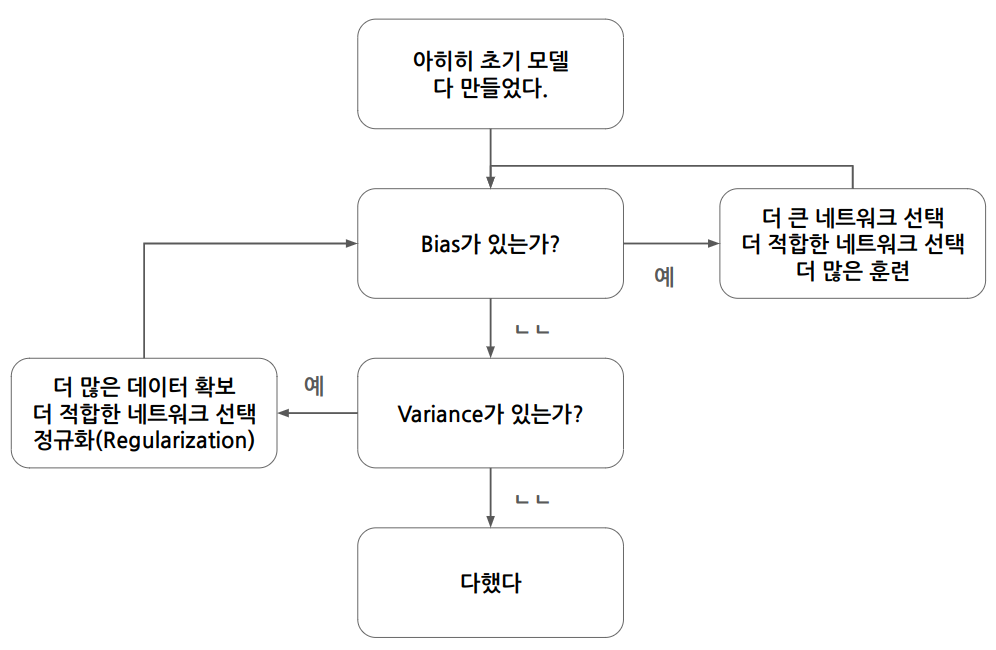
머신러닝 알고리즘 성능을 개선하는 일반적인 순서
1. 초기 모델 훈련
2. high bias 해결 : train set 오류율 확인.
3. high variance 해결 : dev set 오류율 확인.

현대 딥러닝은 bias와 variance를 동시에 낮출 수 있는 도구가 있다.
bias, variance tradeoff문제 해결
딥러닝이 현재 지도학습에서 뛰어난 성능을 보이는 이유 중의 하나임.

정규화로 분산을 낮추고, 더 적합한 아키텍쳐로 편향을 낮춘다.

Regularization

high variance를 해결하기 위한 기법
추가 데이터를 확보하기 어려울 때의 대안이 될 수도 있음.

로지스틱 회귀의 정규화

로지스틱 회귀의 Cost function : $J(w,b) = \frac{1}{m} \sum_{i=1}^m L (\hat{y}^{(i)}, y^{(i)})$

cost function에 regularization term 더하기

• $J(w,b) = \frac{1}{m} \sum_{i=1}^m L (\hat{y}^{(i)}, y^{(i)}) + \frac{\lambda}{2m} ||w||^2_2$
• L2, L1 정규화
  • L2정규화는 L2 norm의 제곱을 쓴다 : $||w||^2_2 = \sum_{j=1}^{n_x} w_j^2 = W^T W$
  • L1정규화는 L1 norm을 쓰는데, 일부 가중치를 0으로 만들어 모델을 압축할 수 있다. 근데 압축목적 아니면 쓰지마라. : $||w||_1 = \sum_{j=1}^{n_x} |w_j|$
• $\lambda$는 정규화 강도 결정. 하이퍼파라미터.

신경망의 정규화

cost function $J(W^{[1]}, b^{[1]}, ... , W^{[l]}, b^{[l]})$

• 정규화 된 cost function : $J(W^{[1]}, b^{[1]}, ... , W^{[l]}, b^{[l]}) + ||w^{[l]}||_F^2$
  • 정규화 항은 프로베니우스 노름의 제곱.
• Frobenius norm : $||w^{[l]}||^2_F = \sum_{i=1}^{n^{[l]}} \sum_{j=1}^{n^{[l-1]}} (w_{i,j}^{[l]})^2$
  • 행렬 내 모든 원소 제곱의 합 (사실상 행렬의 L2 Norm)

정규화된 cost function으로 Gradient Descent를 한다면

• 역전파 : $dw^{[l]} = (원래 그 dw) + \frac{\lambda}{m} w^{[l]}$
• 업데이트 : $w^{[l]} := w^{[l]} - \alpha dw^{[l]}$

L2정규화는 가중치가 조금씩 감소하도록 해서 overfitting을 방지.
그런 의미에서 weight decay라고 부른다.

• 실제 부호있는 값이 아니라, 절대값이 조금씩 감소한다는 것이다.

왜 정규화는 오버피팅을 감소시키나

정규화 매개변수 람다를 크게 만들면, 가중치 W값은 작아진다.
가중치 W가 작아지면 z값이 작아진다.

tanh를 활성화함수로 쓰는 경우, 거의 직선에 가까운 부분만을 취한다.
결국 모델이 단순해진다.

그러나 극도로 단순한 모델을 만드는 것이 아닌, 적당한 복잡도를 가지도록 람다를 결정해야 한다.

Dropout Regularization

L2 정규화처럼 신경망 오버피팅을 방지하는 정규화 기법임. L2정규화의 적응형 형태로 볼 수도. 컴퓨터비전에서 많이 사용. 데이터 충분하지 않아서 오버피팅 될 때 유용.

그게뭐임

• 신경망 각 레이어에서 일부 유닛을 확률적으로 제거. 매번 삭제되는 유닛이 무작위로 달라진다.
• -> 네트워크 크기 줄임
• exmaple마다 서로다른 작아진(축소된) 네트워크에서 학습 -> 모델이 특정 유닛에 과의존 하는 것 방지.
• 일반화된 성능 발휘.

개별 노드의 입장에서 다시 설명

• 나한테 들어올 입력이 무작위로 사라져버릴 수가 있는 어처구니 없는 상황이다.
• 어떤게 사라질지 모르니 특정 입력에 과도하게 의존할 수가 없다.
• 즉, 각 입력에 가중치를 분산시키게 되는 것이며 L2정규화가 그랬듯 가중치제곱 norm을 작게 만든다.

Inverted Dropout 구현

• 드롭아웃 벡터 $d^{[l]}$생성. 각 요소가 keep.prob(노드가 유지될 확률)보다 작은지 확인
• $d^{[l]}$ = np.random.rand(a^l.shape[0], a^l.shape[1]) < keep.prob
• $a^{[l]}$ = np.multiply(a^l, d^l) # bool타입은 사실 곱셈이안됨.
• $a^{[l]} /= keep.prob$ --> inverted dropout이라고 한다.
• 삭제된다 = a의 해당 원소값이 0이 된다 = 가중치를 축소시킨다 = z값이 감소한다

테스트

• 테스트 할 때에는 드롭아웃을 사용하지 않는다. (결과가 무작위로 나올 이유가 없다.)
  대신 스케일링을 한다.
• 근데 inverted dropout은 이미 그게 해결이 돼있다.
  • a의 기대값이 이미 keep.prob으로 미리 나눔으로써 동일해졌으므로, 스케일링 안해도됨.

장단점

• 장점 : 과적합 방지로 일반화된 성능 발휘 가능.
• 단점 : 비용함수 J 정의 어려움. 드롭아웃 매 반복마다 노드가 랜덤하게 사라지니까 그럼. 디버깅도 어려운데, 드롭아웃 끈채로 디버깅해야됨. 디버깅끝나면 드롭아웃 다시 켜줘야됨.
  • 드롭아웃 끈다 = keep_prob값 1로 주기.

다른 정규화 기법

Data Augmentation (데이터 증강)

• 기존 train set을 변형해서 새로운 train set 생성.
• e.g., flip, random crop, rotate
• 당연히 진짜 새로운 데이터 얻는것보단 별론데, 데이터없으면 이거라도 써야지 뭐..

Early Stopping

• 경사하강법 실행하면서 train set 에러랑 dev set 에러 관찰함.
• 학습 진행될수록 train set에러는 계속 감소함
  • 근데 dev set에러는 어느 순간 증가하기 시작할 수 있음.
  • 이 때 훈련 멈추면 -> 최적의 dev set 성능이 나온다.
• 중간에 멈춘다 = 가중치w가 학습이 진행됨에 따라 점점 커지는데, 어느순간 멈춰서 더 안커지게함
  • 즉, 과적합 방지.
• 문제 : 비용함수J 최적화 문제와 과적합 문제를 독립적으로 다루기 어려워짐
  • 이거 싫으면 L2정규화 쓰든지
  • 그러나 L2정규화의 문제 : 람다값 계산하는 비용이 크다.

Setup Optimization Problem

Normalizing Inputs

피쳐들의 단위가 다 제멋대로 일 때 동일한 기준으로 맞춰주는 것.

왜함? : 학습빨라짐.

• 비용함수 최적화
• 경사하강법 효율성. (더 큰 스텝으로 움직여서 빠른 수렴 가능)
• 고차원 공간에서의 이점. (비용함수 동글동글해지니까 최적화 쉬워진다.)

주의

• train set, test set 모두 동일한 μ, σ로 정규화해야됨.

Zero-centering the mean (평균 빼기)

• $\mu = \frac{1}{m} \sum_{i=1}^{m} x^{(i)}$
• $x^{(i)} := x^{(i)} - \mu$

Normalizing the variance (분산정규화)

• $\sigma^2 = \frac{1}{m} \sum_{i=1}^{m} (x^{(i)} **2)$ : **2는 element-wise squre
• $x^{(i)} := x^{(i)} / \sigma^2$

Vanishing(소실) / Exploding(폭발) Gradients

모델 학습 중에 기울기의 크기가 너무 극단적이어서 학습이 안될 수 있음.

• 기울기가 너무 작아져서(Vanishing)
• 반대로 기울기가 너무 커져셔(Exploding)

초기 가중치 W를 잘 정해서 이 문제를 어느정도 완화할 수 있음

• 랜덤하게 초기화

Weight Initialization for Deep Networks

가중치의 초기값을 어떻게 정할까에 대한 고민

기본 전제 :

• 입력이 많아질수록 각 입력의 가중치 $w_i$는 작아져야됨.
• W의 분산을 1/n으로 하자.

참고

• np.random.randn( shape )이 뱉는걸 가우시안 랜덤 변수라고 한다.

일반적인 경우

• $W^{[i]}$ = np.random.randn( shape ) $*$ np.sqrt(${1 / n^{[l-1]}}$)

g(z) = ReLU

• $W^{[i]}$ = np.random.randn( shape ) $*$ np.sqrt(${2 / n^{[l-1]}}$)

g(z) = tanh

• 위의 일반적인 경우를 써도 된다.
• Xavier 초기화 방법 : $W^{[i]}$ = np.random.randn( shape ) $*$ np.sqrt(${2 / (n^{[l-1]} + n^{[l]})}$)

초기화 파라미터 튜닝

• np.sqrt(${(PARAM \times 1) / n^{[l-1]}}$)
• 대충 뭐 이렇게 생긴 저 식은, 가중치행렬에 초기 분산을 먹이기 위한 것임
• 원한다면 분자에다가 뭔가 곱해도 됨
  • 그럼 곱하는 그게 또 하나의 하이퍼파라미터가 된다.

Gradient checking

back propagation구현이 올바른지 확인하기 위해 gradient checking을 할 수 있음.
일종의 테스트로 보면 됨.
(주의)

• 이거 완전느리니까 학습 때 쓰면 안된다. 디버깅 할 때 써라.
• 드롭아웃 정규화를 하는 경우, Grad checking과 호환 안됨. 굳이 체킹하고싶으면 드랍아웃 끄고하셈. (호환되게 하고싶으면 뭐 특별한 작업필요한데 알아서하셈)
• 파라미터 랜덤초기화 하는 경우 : 몇 번 이터레이션 돌려서 W,b값을 0에서 멀어지게 만든 뒤(키운뒤) grad checking해볼것.

벡터 합치기

• 순전파에서 모든 매개변수 W, b를 합쳐서 하나의 매개변수 벡터 $\theta$를 만든다.
• 역전파도 모든 미분값 dW, db를 합쳐서 하나의 벡터 $d\theta$로 만든다.

비용함수를 다시 쓰면

• $J(W^{[1]}, b^{[1]}, ... , W^{[l]}, b^{[l]}) = J(\theta)$

이제 할 일

• $d\theta$는 비용함수 $J(\theta)$의 기울기가 맞냐? 를 알아보도록하자

구현

• 경사의 근사치 구하기
  • $d\theta_{\text{approx}} = \frac{J(\theta_1, \theta_2, \ldots, \theta_i + \epsilon, \ldots) - J(\theta_1, \theta_2, \ldots, \theta_i - \epsilon, \ldots)}{2\epsilon}$
• 실제 경사와 근사치 비교 (벡터 거리 계산)
  • CHECK : $\frac{\| d\theta_{\text{approx}} - d\theta \|}{\| d\theta_{\text{approx}} \| + \| d\theta \|}$
• 위에서 계산된 값에 따라 판단
  • $10^{-7}$ 이하 : 굳
  • $10^{-5}$ 정도 : 점검필요
  • $10^{-3}$ 이상 : 버그 있을가능성 높음.

Optimization Algorithms

mini-batch gradient descent

기존에 학습한 경사하강법 ( = batch gradient descent )

• 기존의 경사하강법은 전체 데이터셋을 한 뭉치로 돌렸다.
• 경사하강법을 실행할 때, 전체 데이터셋에 대해 한 단계를 처리해야만 다음 단계를 수행할 수 있다.

mini-batch의 개념

• 데이터셋 개수가 많아지면 이거 너무 답답하니까, 데이터셋을 나눈다
• 나눠진 각각의 데이터셋을 mini-batch라고 한다.
• 표기 : $X^{\{t\}}$와 같이 한다. t는 1부터 시작하는 미니배치 번호
  • 예시 : m=5000이고 한개 미니배치가 1000개 데이터를 가지면
  • 미니배치는 $X^{\{1\}}, X^{\{2\}}, ..., X^{\{5\}}$ 총 5개가 있다.
  • $X^{\{1\}}$는 데이터셋$x^{(1)}$ ~ $x^{(1000)}$ 을 포함한다. 그럼 shape는 (피쳐 개수, 1000)이 되겠다.
• $X^{\{t\}}, Y^{\{t\}}$ 미니배치에 대해 경사하강법을 돌리면 비용 $J^{\{t\}}$가 나온다.

epoch

• 전체 training set에 대해 전부 학습을 돌리는 것. 그 1번의 반복을 1 epoch라고 한다.
• m=5000이고 미니배치가 5개라고 하자. 미니배치 1~5번을 모두 학습돌렸으면 그 때 1 epoch를 돈 것.

그래서 많이씀?

• 훈련세트가 많다면 미니배치 경사하강법이 훨씬 빠르다. 사람들이 이거 많이한다.
• 딥러닝은 빅데이터에서 잘 동작하는데, 빅데이터는 너무 크기 때문.

미니배치 경사하강법의 cost function 변화

• 전체적으로 보면 하강하는 추세.
• 그러나 매 미니배치마다 약간씩 증가했다 감소했다 한다. (노이즈가 껴있다.)

미니배치 크기

• 극단적인 경우 보기
  • 전체 데이터셋 크기 m과 같으면 : batch gradient descent임 그냥 (시간오래걸림)
  • 1이면 : SGD(확률적 경사하강법)임 그냥 (하나씩 처리하므로 노이즈 많고 느림)
  • 그래서 미니배치 경사하강법을 하겠다 하면 1 < 미니배치_크기 < m을 하십쇼.
• 선택 가이드라인
  • m <= 2000 정도로 데이터 작으면 : 그냥 배치 경사하강법 하십쇼
  • 데이터가 너무많다면 : $2^6, 2^7, 2^8, 2^9$ 해보고 좋은거 쓰십쇼.
• 선택 주의사항
  • cpu gpu, 메모리가 버틸지 확인. 메모리 초과하는 크기면 성능 급하락
• 미니배치 크기는 사실상 하이퍼파라미터임. 잘 찾아보시지

Exponentially Weighted Moving Averages

$V_t = \beta V_{t-1} + (1 - \beta) \theta_t$
$V_0 = 0$
$0 < \beta < 1$

$\theta_t$는 t번째 데이터 값을 말함.
$\beta$가 하이퍼파라미터인데, 어느정도 범위의 평균을 낼 것이냐를 말함.

• $V_t$는 대략 $1 / (1-\beta)$개 데이터의 평균을 냄.
• 즉, $\beta$가 커질수록 더 많은 데이터의 평균을 내고, 변화에 따른 반응이 느려짐
• 반대로 $\beta$가 작아지면 작은 데이터의 평균을 내고, 변화에 빨리 반응함. 노이즈도 커짐.

V = 0
beta = 0.9  
theta = [40, 42, 44, 46, 48]

for t in range(len(theta)):
    V = beta * V + (1 - beta) * theta[t]
    print(f"V{t + 1} = {V}")

좋은점 :

• 메모리 효율적(단일 실수값만 유지하면 되니까)
• 구현 간단함

그러나 평균을 구하는 가장빠르고 최고의 방법이라는건 아님

• 데이터 몇개 평균 구하고싶으면, 사실은 우리가 늘 해오던대로 t번째 데이터 이전, 이후 데이터들 싹 더해서 평균내면 된다.
• 근데 그러면 메모리를 너무많이 잡아먹는 것이다
• 그래서 메모리가 중요하면 지수가중이동평균을 쓴다.

bias correction (편향 보정)

• V0 = 0일 때 문제 : 학습 초기에 값을 이상하게 예측함 (실제값보다 작게)
• 그래서 편향 보정을 해준다.
  • $\hat{V}_t = \frac{V_t}{1 - \beta^t}$
  • t가 커질수록 편향보정의 효과는 사라진다.
• 근데 사람들 잘 구현 안한다고 한다. 걍 처음에 이상한값 버리고, 정상적인 구간부터 사용함.

Gradient Descent with Momentum

gradient의 지수 가중 평균을 계산한 후, 이를 사용하여 가중치 업데이트.
대부분의 경우, 그냥 그라디언트 디센트보다 빠르게 수렴한다.

그냥 경사하강법에 대한 불만

• 수직 방향으로 진동하며 느리게 수렴.
  • 러닝레이트가 낮다
• 모멘텀 알고리즘을 통해서
  • 가야되는 방향에 큰 가중치를 두고 기울기를 구해서 빠르게 최소값에 도달하고자 함.
  • = (불필요한) 진동을 줄인다
  • = 최소값으로 가는 올바른 방향에 가속을 준다.

모멘텀 알고리즘 구현

• 지수가중평균 구하기

  • $V_{dW} = \beta V_{dW} + (1 - \beta) dW$
    • $V_{dW}$는 속도, $dW$는 가속도로 비유 가능.
    • $0<\beta<1$는 마찰의 기능. 무한히 가속이 붙지 않게 함. 0.9정도면 잘 작동함. (한 번에 적당히 학습 먹입시다)
  • $V_{db} = \beta V_{db} + (1 - \beta) db$

• 파라미터 업데이트하기

  • $W = W - \alpha V_{dW}$
  • $b = b - \alpha V_{db}$

• 참고

  • 편향보정은 잘 안함.
  • 평균 구할 때 뒷 항에서 $(1-\beta)$를 생략하고 $dW$, $db$만 쓰는 경우가 있는데, 그냥 그런갑다 하셈.

RMSprop

모멘텀 알고리즘이랑 거의 똑같다. 식만 다르다.

구현방법

• 지수가중평균 구하기
  • $S_{dW} = \beta_2 S_{dW} + (1 - \beta_2) dW^2$
  • $S_{db} = \beta_2 S_{db} + (1 - \beta_2) db^2$
• 업데이트
  • $W = W - \alpha\frac{ dW}{\sqrt{S_{dW}} + \epsilon}$
  • $b = b - \alpha\frac{ db}{\sqrt{S_{db}} + \epsilon}$

참고

• $\beta_2$ : 그냥 파라미터인데, 모멘텀 알고리즘의 베타랑 헷갈려서 아래첨자 2 붙인거.
• $\sqrt{S_{dW}}$가 0이되면 폭발할수있음. 분수 0으로 안나누게 주의.
• $\epsilon$은 $10^{-8}$정도면 합리적. 약간 더 커도 수학적 안정성 보장됨.

Adam Optimization Algorithm

모멘텀 알고리즘, RMSprop을 결합한 알고리즘.
두개 장점 결합해서 성능 괜찮음. 많이들 씀.

파라미터 추천값

• $\alpha$ : 알아서 하십쇼. 튜닝 화이팅
• $\beta_1$ : 0.9 (모멘텀 베타)
• $\beta_2$ : 0.999 (RMSprop 베타)
• $\epsilon$ : $10^{-8}$ (안해도 큰 상관없긴함)

구현

• 늘 하던 그 평균 구하기
  • $V_{dW} = \beta_1 V_{dW} + (1 - \beta_1) dW$
  • $V_{db} = \beta_1 V_{db} + (1 - \beta_1) db$
  • $S_{dW} = \beta_2 S_{dW} + (1 - \beta_2) dW^2$
  • $S_{db} = \beta_2 S_{db} + (1 - \beta_2) db^2$
• 편향 보정
  • $\hat{V}_{dW} = \frac{V_{dW}}{1 - {\beta_1}^t}$
  • $\hat{V}_{db} = \frac{V_{db}}{1 - {\beta_1}^t}$
  • $\hat{S}_{dW} = \frac{S_{dW}}{1 - {\beta_2}^t}$
  • $\hat{S}_{db} = \frac{S_{db}}{1 - {\beta_2}^t}$
• 업데이트
  • $W = W - \alpha\frac{ \hat{V}_{dW}}{\sqrt{\hat{S}_{dW}} + \epsilon}$
  • $b = b - \alpha\frac{ \hat{V}_{db}}{\sqrt{\hat{S}_{db}} + \epsilon}$

Learning Rate Decay (러닝레이트 감쇠)

미니배치 경사하강법 할 때 문제

• 러닝레이트가 고정되어 있음
• 그럼 진동하면서 수렴을 못하고, 무한히 빙빙 도는수가 있음.

그럼 어떻게할까

• 초기에는 러닝레이트를 크게 주고, 점차 줄여버리자.
• 학습이 진행될수록 러닝레이트를 줄인다는 이야기다.
• 그럼 최소값 주변에서 안정적으로 수렴한다.

초기 러닝레이트

• $\alpha_0$라고 하자

구현방법

• Linear Decay : $\alpha = \frac{1}{1 + \text{decay rate} \times \text{epoch number}} \alpha_0$
• Exponential Decay : $\alpha = \alpha_0 \times 0.95^{\text{epoch num}}$
• $\alpha = \frac{k}{\sqrt{\text{epoch num}}} \times \alpha_0 = \frac{k}{\sqrt{\text{t}}} \times \alpha_0$
• Discrete Staircase Decay
• 직접 감쇠 : (최첨단 인간지능) 모델 훈련중에 성능 봐가면서 수동으로 조절
  • 이거 학습양이 (비교적) 작은 경우에만 할수있음. 백날 붙어있을거 아니니까.

The problem of local optima

사람들이 머신러닝 학습에서 local optima를 걱정하고는 하는데
local optima 만날 확률은 고차원 데이터를 다룰 수록 적어진다.
1000차원이라면, 1000방향으로 모두 내려와야 비로소 local optima이기 때문

경사가 0인 지점은 대부분 saddle point다.
saddle point는 학습이 중단되지는 않지만, 평지와 같아서 학습이 매우 느리다.
빨리 벗어나기 위해 최적화 알고리즘의 도움을 받는다. 모멘텀, Adam같은 것들.

Hyperparameter Tuning

딥러닝 모델을 훈련시킬 때 설정해야 할 하이퍼파라미터가 많이 있다.
러닝레이트 $\alpha$가 가장 중요하고, 모멘텀 베타, 미니배치 크기, 히든유닛수 $n^{[l]}$ 등이 그 뒤를 따른다.

Tuning Process

하이퍼파라미터 탐색 방법의 예

• Grid Search
  • 이전세대 머신러닝에서 많이 사용했음
  • 고정된 간격으로 모든 조합 시도 (그러나 충분히 다양한 값을 시도한다는 보장은 없음)
• Random Search
  • 딥러닝에서 특히 효율적인 탐생방법.
  • 어떤 하이퍼파라미터가 중요한지 사전에 알기 어려우므로 랜덤하게 샘플링하는 것
  • 다양한 값 시도 가능.
• Coarse-to-Fine Search
  • 처음에 넓은 범위를 샘플링해서 좋은 성능이 나오는 지역 선정
  • 선정한 지역을 더 세밀하게(집중적으로) 샘플링

랜덤 서치를 기본적으로 사용하고, 필요시 코스투파인을 사용.
체계적으로 하이퍼파라미터 탐색을 조직화하는 것이 최적 값을 찾는데 도움됨.

Using an Appropriate Scale to Pick Hyperparameters

하이퍼파라미터 샘플링 시 적절한 스케일 사용 중요
랜덤샘플링 시 사용할 척도 설정방법.

• 선형 스케일
  • 있는그대로의 범위 전체에서 균일하게 값을 뽑아서 보면 좋은 경우에 사용
  • e.g., 은닉층 유닛 수 등
• 로그 스케일
  • 범위의 일부분에서 유의미한 값이 나오는 경우
  • 값이 조금만 바뀌어도 결과가 크게 변하는 경우
  • 로그 스케일로 보면 좁은 부분에 대해 마치 선형스케일처럼 탐색할 수 있음.
  • e.g., learning rate는 0~1 사이지만, 0.1~1의 탐색에 90%의 컴퓨팅자원을 쓸 이유는 없다.
  • e.g., momentum 파라미터 beta는 0.9 이후로 결과가 엄청나게 바뀌어버린다.

Batch Normalization

• (주의) 여기서 쓰는 베타는 모멘텀알고리즘의 베타와 다름.

개념

히든레이어의 활성화값 a, 정확하게는 중간값 z를 정규화한다

• 그러면 가중치 w, b의 학습이 더 효율적으로 동작.

구현

• 평균 계산 : $\mu = \frac{1}{m} \sum_{i=1}^{m} z^{(i)}$
• 분산 계산 : $\sigma^2 = \frac{1}{m} \sum_{i=1}^{m} (z_i - \mu)^2 \\$
• 정규화 : $z^{(i)}_{\text{norm}} = \frac{z^{(i)} - \mu}{\sqrt{\sigma^2 + \epsilon}}$ ---> 평균0, 표준편차1
• 스케일링, 이동 : $\tilde{z}^{(i)} = \gamma z^{(i)}_{\text{norm}} + \beta$

감마, 베타는 모델에서 (경사하강법 같은걸로)학습시킬 수 있는 파라미터.
조절하면 $\tilde{z}^{(i)}$의 평균 원하는대로 조작가능.

• 감마는 스케일링
• 베타는 쉬프트

결국, 배치 정규화는

• 입력뿐 아니라 은닉층의 활성값도 정규화하는 것이며
• 표준화된 평균, 분산을 가지면서, 동시에 파라미터에 따라 평균과 분산을 조절하는 것.

실제 딥뉴럴네트워크에서 쓰일 때는

• 순전파

  • 배치 정규화 과정에서 z값의 평균이 0로 조정됨
  • 기존에 있던 잔차 파라미터 b는 항상 상쇄됨
  • 그래서 각 레이어에서 b대신 $\beta$가 대신 사용됨

• 역전파

  • 원래 dw db 계산했었는데
  • 이제는 dw d$\beta$ d$\gamma$를 계산한다.

왜 효과적인가?

• 학습 속도 빨라짐 : 정규화가 되니까.
• Internal Covariate Shift (내부 공변량 변화) 문제 완화
  • 내부공변량변화 = 각 레이어에서 입력의 분포가 변화하는 것.
  • 배치정규화는 분포를 정규화하니까 이 문제가 완화됨.
    • 다시 말하면, 앞 레이어와 뒤 레이어의 관계를 약화시킴. 영향을 덜받음. (각 층이 스스로 배운다)
    • 뒤 레이어 입장에서, 입력이 덜 변한다.
• 기울기 소실, 폭발 문제 완화
• 규제효과
  • 드롭아웃 정규화처럼 오버피팅 줄이는데 도움됨.
  • 노이즈 추가됨
  • 배치 정규화로 일반화가 되긴하는데, 부수적인 효과에 불과하다. 좀 크긴한데..
    • 아무튼 배치정규화는 일반화 목적이 아니다. 그 목적으로 쓰지마라.
• 미니배치에서 평균, 분산 사용
  • 배치정규화는 각 미니배치에서 계산된 값을 갖고 정규화를 함.
  • 쪼개서 할수있으니까 online learning도 되겠다.

테스트시 개별 데이터에 대해 배치정규화 적용

학습 때에 미니배치 단위로 평균, 분산을 원래 하던대로 계산
이걸 지수가동이동평균 내서 평균, 분산 각각 유지.

하던대로 그대로 하는데, 다만 평균, 분산의 지수가동이동평균을 유지해주라는거다.

• 평균 계산 : $\mu = \frac{1}{m} \sum_{i=1}^{m} z^{(i)}$
• 분산 계산 : $\sigma^2 = \frac{1}{m} \sum_{i=1}^{m} (z_i - \mu)^2 \\$
• 정규화 : $z^{(i)}_{\text{norm}} = \frac{z^{(i)} - \mu}{\sqrt{\sigma^2 + \epsilon}}$ ---> 평균0, 표준편차1
• 스케일링, 이동 : $\tilde{z}^{(i)} = \gamma z^{(i)}_{\text{norm}} + \beta$

지수가동이동평균 변수이름이 $\mu$, $\sigma^2$ 라고 하자.
그럼 개별 데이터에 대한 배치정규화 값을 구하면

• $z_{\text{norm}} = \frac{z - \mu}{\sqrt{\sigma^2 + \epsilon}}$ ---> 평균0, 표준편차1
• $\tilde{z} = \gamma z_{\text{norm}} + \beta$

Multi-class Classification

여러개의 클래스를 분류하는 경우 Softmax Regression사용 가능
로지스틱 회귀를 일반화한것으로 생각할 수 있음
출력으로 확률분포를 뱉음.

소프트맥스 레이어

소프트맥스 레이어는 네트워크의 output레이어.
각 클래스에 대한 확률을 출력

• 이 때, 지금까지 봐왔던 출력층은 실수(real number) 받아서 실수 출력했음
• 근데 소프트맥스 (활성화)함수는 벡터 받아서 벡터 출력함
  • 왜냐면 클래스가 여러개고, 각 클래스별로 확률을 담아서 뱉어야되기 때문
  • 벡터 원소의 (노드별) 각 값은 그 클래스가 맞을 확률을 말함.
  • 노드별 값들 다 더하면 1임.(확률이니까)

소프트맥스의 활성화 값 $a^{[L]}$을 구하기까지 (출력층이니까 $l=L$이다)

• C : 클래스의 개수 ($C=4$이면 데이터를 4가지 클래스로 분류)
  • $C=2$이면 로지스틱 회귀가 된다.
• 선형계산 : $z^{[L]} = w^{[L]} a^{[L-1]} + b^{[L]}$
• 지수함수 적용 : $t = e^{z^{[L]}}$
  • 여기서 t는 C차원의 벡터가 될 것임. 즉, t의 원소는 $t_1$부터 $t_{C}$까지 C개가 있다.
• 정규화 : $a^{[L]} = \hat{y} = t / ({\sum_{i=1}^{C} t_i})$
  • 벡터a도 C차원이다. 원소 각각이 '이 클래스가 맞을' 확률을 담고 있다.

학습을 위한 공식을 살펴보면

• Loss function : $L = -\sum_{j=1}^{C} y_j \log(\hat{y}_j)$
• Cost function : $J = \frac{1}{m} \sum_{i=1}^{m} L(\hat{y}^{(i)}, y^{(i)})$
• $dZ^{[L]}$ = $\frac{\partial J}{\partial Z^{[L]}} = \hat{y} - y$

이제 정의가 끝났으니 이걸로 모델 구현해서 학습 열심히 돌리면 된다.

TensorFlow

좋은점 : 순전파만 구현하면 역전파는 텐서플로우가 알아서 해준다