• 앤드류 응 Deep Learning Specialization의 강의 1
• 구글 MLB DLS 미션1

강의 자막 참고 :

• 한국어 자막이 제공되지만, 안보느니만 못합니다.
• 영어 자막이 제공됩니다. 한국어 자막보다는 낫지만, 오타가 정말 많습니다.
• 잘못하면 터미놀로지 자체를 잘못 배웁니다.
• 그러니 자막없이 그냥 영어듣기평가 하듯이 수강하시는 것이 가장 현명합니다.
• 자막이 그닥 쓸모가 없습니다.

Introduction to Deep Learning

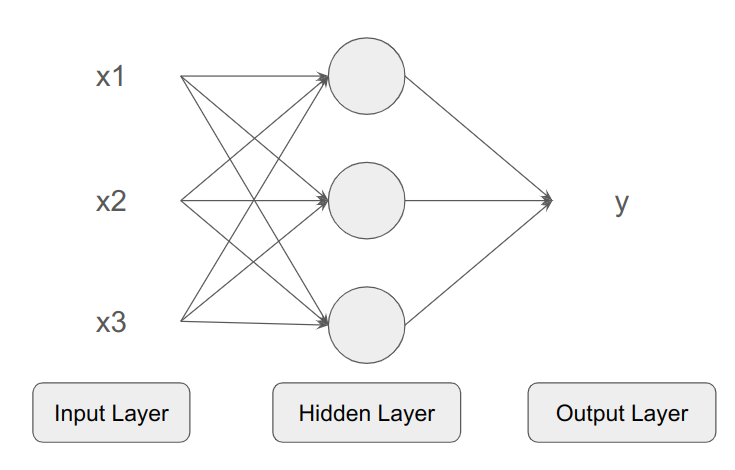
가장 단순한 뉴럴 네트워크

• Standard NN
• 뉴런은 입력을 받고 출력을 뱉는다.
• 뉴런을 쌓으면 레이어가 된다.
• 레이어가 모이면 뉴럴네트워크(NN, 인공신경망)으로 부른다.
  • input, hidden, output 레이어

아래 뉴럴네트워크는 은닉층의 각 뉴런이 모든 x(feature)로부터 입력을 받는다.

• 사람이 특정 노드에 적합한 x를 고르지 않는다.
• 뉴럴네트워크가 적절한 x를 골라 적절한 출력을 내도록 맡긴다.
• 트레이닛 셋(x to y)을 주면, x로부터 y로의 매핑을 한다.

Supervised Learning

Input(x), Output(y) 데이터를 주고 훈련시킨다. 일반적인 예를 들면

• Standard NN : 온라인광고
• Convolutional NN (CNN) : Image
• Recurrent NN (RNN) : 음성인식, 기계번역 (시간 등 순서가 있는 것들)

데이터는 두 가지로 분류한다

• Structured Data : 일반적인 테이블 DB
• Unstructured Data : 오디오, 이미지, 텍스트

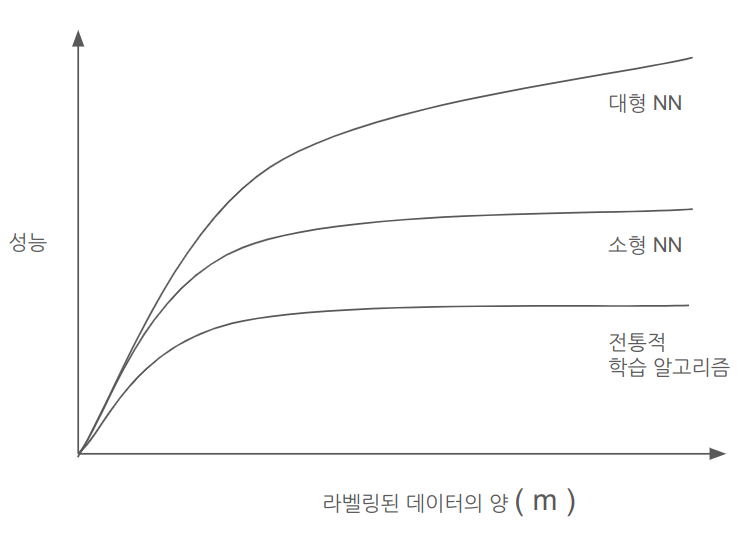
딥러닝은 왜 잘나가나

머신러닝의 구현 방법에 따라, 라벨링된 데이터의 양에 따른 성능이 다르다.

• 데이터셋이 작은 경우 SEM이 나을 수 있다. 개발자 스킬의 영향이 크다.
• 규모가 딥러닝의 발전을 견인한다.

딥러닝이 이제와서 잘나가는 이유로 세 가지를 꼽는다면

• Data : 더 대규모의 데이터
• Computation : 연산이 빠를 수록 Idea-Code-Experiment 사이클을 빨리 돌릴 수 있음
• Algorithms : 연산 성능을 올릴 수 있음 (e.g., sigmoid to ReLU)
  • ReLU (Rectified Linear Unit) : max(0, x)인 함수

약자는

• m : 데이터셋 크기 (traing examples의 수)

Logistic Regression as a NN

Neural Network Basics - part 1 of 2

Binary Classification

Logistic Regression은 Binary Classification을 위한 알고리즘
입력을 받아 0, 1 중 한 개 출력

• e.g., 이미지 입력받아서 0(고양이 아님), 1(고양이 맞음) 출력

Binary Classification을 위한 Notation

• $n_x$ : x ($_{\text{ input feature vector }}$)의 차원 (=한 입력 단위는 몇 개의 피쳐가 모여 구성되느냐?)
  • e.g., 4X4 rgb이미지의 $n_x$
    • $= \text{가로 비트수}\times\text{세로 픽셀수}\times{\text{rgb 3개}}$
    • $= 4\times4\times3 = 48$
  • $x \in \R^{n_x}$
  • $y \in \{ 0, 1 \}$
• m : 데이터셋의 수
  • m training examples $= \{(x^1, y^1), (x^2, y^2), ... ,(x^m, y^m)\}$
  • $M_{train}$ : train example의 수
  • $M_{test}$ : test example의 수
• 입력 벡터 $X$
  • $X \in \R^{n_x \times m}$
  • $X = \begin{bmatrix}x^1_1 & x^2_1 & ... & x^m_1 \\ x^1_2 & x^2_2 & ... & x^m_2 \\ ... & ... & ... & ... \\ x^1_{n_x} & x^2_{n_x} & ... & x^m_{n_x} \\ \end{bmatrix}$
    • $= \begin{bmatrix} x^1 & x^2 & ... & x^m \end{bmatrix}$
    • X.shape = (n_x, m)
    • 열(col) 방향 = ($m$) : 다른 입력x의 나열
    • 행(row) 방향 = ($n_x$) : 같은 입력x의 각 피쳐 나열
  • 다른 사람들은 $X$대신 $X^T$의 형태로 입력을 넣기도 함.
• 출력 벡터 $Y$
  • $Y \in \R^{1 \times m}$
  • $Y = \begin{bmatrix} y^1 & y^2 & ... & y^m \end{bmatrix}$
    • Y.shape = (1, m)

Logistic Regression Model

은 Sigmoid함수를 쓴다

• $\hat{y} = \sigma (z) =\frac{1}{1+e^{-z}}$
  • 입력 $z = w^T \times x$에 대해서
  • 0~1 사이의 출력 $\hat{y}$를 낸다.

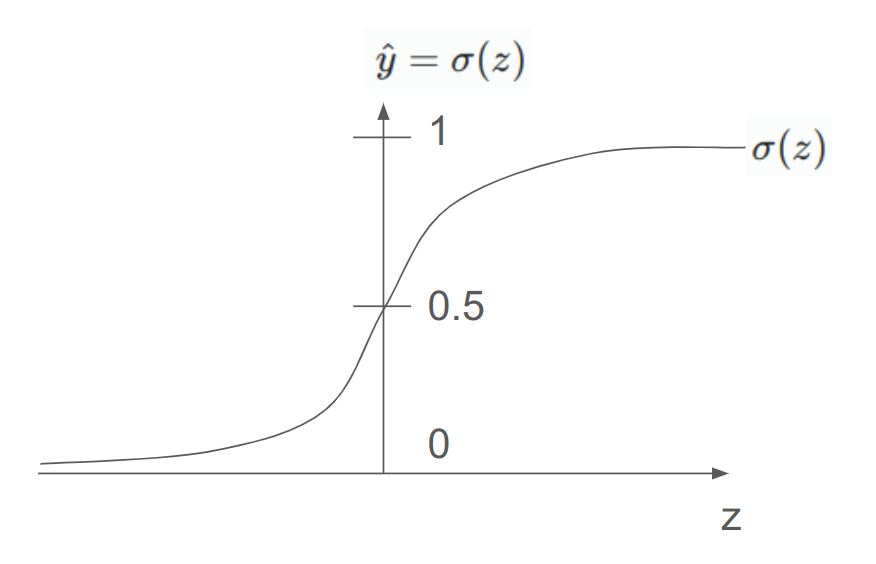
구하려는 출력값이 무엇인지부터 정의하자.
$\hat{y}$은 주어진 입력 $x$에 대해 예측된 출력 $y$(ground truth).
$\hat{y} = P(y=1 | x)$을 구하고 싶다.

• 입력x가 주어졌을 때 예측된 출력 $y$가 1일 확률
• 즉, $0 \le \hat{y} \le 1$

로지스틱 리그레션의 파라미터는 2개

• $w \in \R^{n_x}$
• $b \in \R$

여기서 $z=w^T x + b$라고 하면

• $\hat{y} = \sigma (z)$
  • $=\frac{1}{1+e^{-z}}$
  • When $z=\infin$, $\sigma(z) = 1$
  • When $z=-\infin$, $\sigma(z) = 0$

w와 b를 구하기 위해 이제 cost function이 필요해진다.

Logistic Regressioin Cost Function

Loss(error) function :

• 한 개 example에 대한 실제 정답($y$)과 예측치($\hat{y}$)의 오차를 계산하는 함수.
• 작을 수록 좋음. 오차가 적다는 말이니까.
• $\mathcal{L} (\hat{y}, y) = -(ylog(\hat{y}) + (1-y)log(1-\hat{y}))$
  • 이게 왜 맞음?
  • y=1 넣으면 $\hat{y}$이 1에 가까워질 수록 손실함수 값 작아짐
  • y=0 넣으면 $\hat{y}$이 0에 가까워질 수록 손실함수 값 작아짐

Cost function : 전체 트레이닝 example들에 대한 오차를 계산

• $J(w, b) = \frac{1}{m} \sum\limits_{i=1}^m {\mathcal{L} (\hat{y}^i, y^i)}$

이제 이 Cost function을 이용해서 학습을 진행한다.

• 다시 말하면, Cost function $J(w,b)$를 가능한 작게 만드는 $W$와 $b$를 찾는다.
• 그 알고리즘의 이름이 Gradient Descent다.

convex, non-convex 함수

함수가 하나의 minimum을 갖는 경우 convex function이라고 한다.
여러개의 minimun (local optimal)을 갖는 경우 non-convex function이라고 한다.

위에서 Logostic Regression에 대해 정의한 Cost function $J$는 convex하다.

Gradient Descent 알고리즘 (경사하강법)

로지스틱 리그레션의 cost function이 convex function이므로 Gradient Descent로 최적의 W, b를 찾아볼 수 있다.

여러 번의 이터레이션을 돌면서 (step을 밟으면서)

• 가장 가파른 하강 방향으로 내려간다. (try to take a step downhill in the direction of steepest descent as quickly as possible)
• 내려간다는 것은, w와 b값을 새로이 업데이트 하는 것이다.
• 결국에는 minimum(혹은 근접한 점)을 찾는다.

업데이트 하는 것을 수식으로 표현하면 아래와 같다.

• $w := w - \alpha \frac{\partial{J(w,b)}}{\partial{w}}$
  • $= w - \alpha\ d\text{w}$
  • 빼는 값을 $dw$라고 표기하자.
  • alpha는 step을 얼마나 빠르게 밟을 것인지를 결정
• $b := b - \alpha \frac{\partial{J(w,b)}}{\partial{b}}$
  • $= b - \alpha\ d\text{b}$

$d$w와 $d$b는 아래 back propagation을 통해 얻는다.

computation graph

뉴럴네트워크의 컴퓨테이션은 forward propagation, back(ward) propagation으로 구성
computation graph는 왜 그렇게 구성되어있는지 설명함.

forward propagation은 단계적으로 변수를 계산하고, 결국에는 최종 변수를 계산
back propagation은 거꾸로 단계를 거슬러가며 각 변수의 최종변수에 대한 미분을 계산

참고 : computational graphs in deep learning - geeksforgeeks

약속
$\frac{d\ \text{FinalOutputVar}}{d\ \text{var}}$는 $d$ var 라고 표현하자.
최적화하기를 원하는 최종 변수가 J이고 a로 미분한 결과를 알고 싶다면 $d$ a라고 한다.

계산 전 함수 f, 변수 x~z, a~d 정의

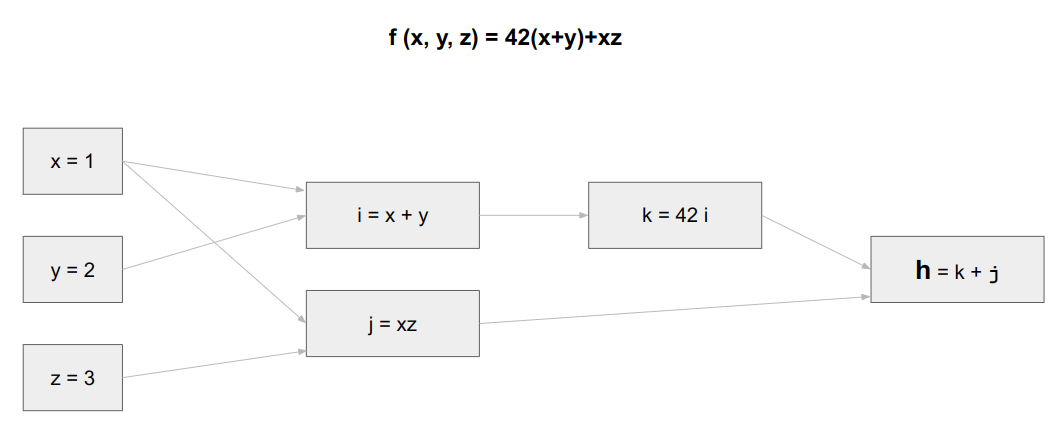
forward pass (propagation).

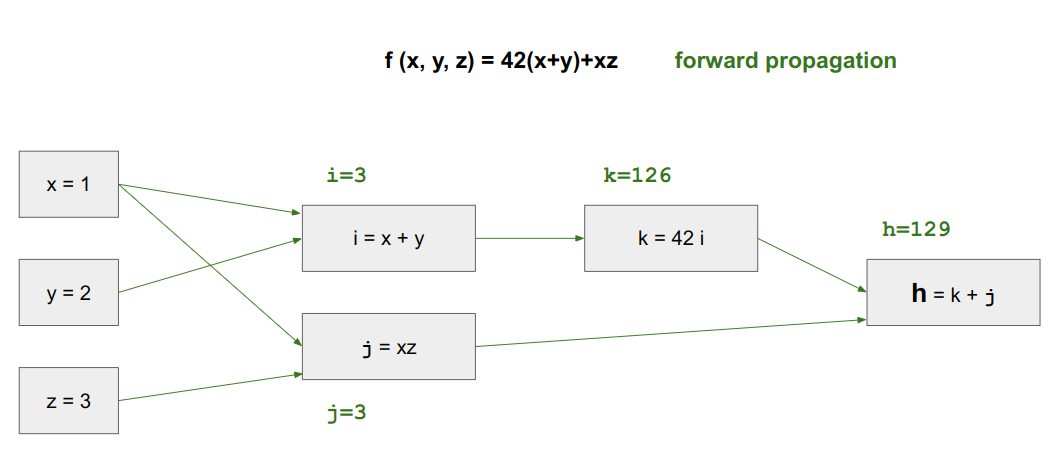
backward pass (progagation)

• 복잡해 보이지만 그냥 체인룰 덕지덕지다.
  

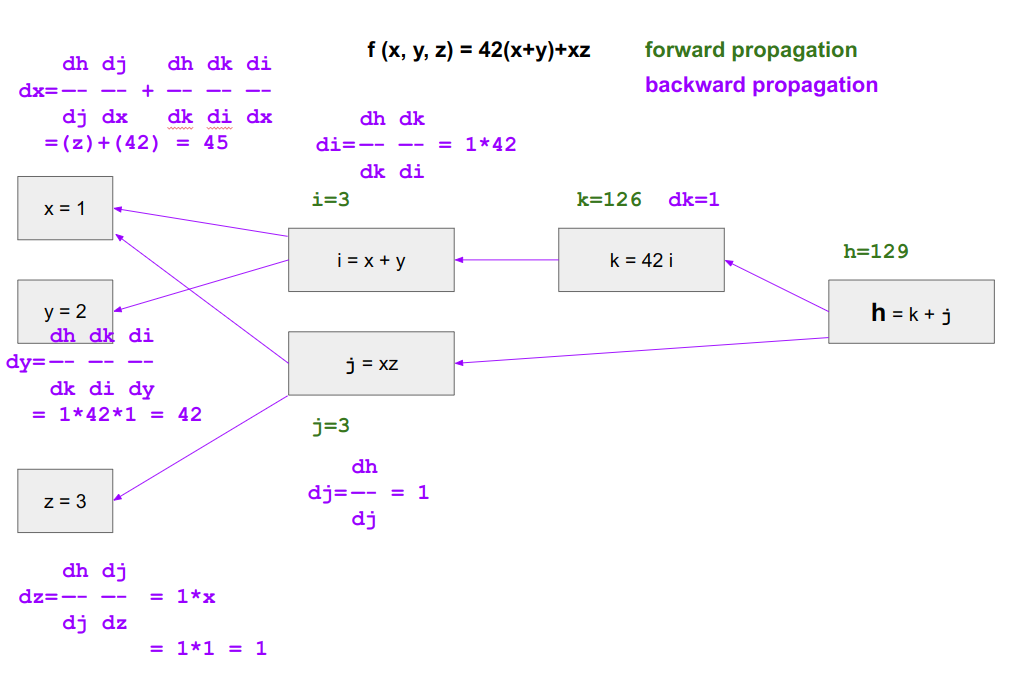
로지스틱 리그레션의 로스함수로 w, b를 최적화 할 때에도 위와 같은 과정을 따른다.

• 로스값을 구한다. (forward)
• 로스값이 나왔으면 입력 w, b방향으로 미분을 한다. (back)
• 미분된 값을 기존의 w, b에서 뺀다. (update)
• 그 상태가 w, b가 한 step을 밟아 업데이트 된 것이다.

cost함수로 모든 트레이닝 examples에 대해 w, b를 최적화 할때도 마찬가지다.
그냥 여러 번 할 뿐이다.

• training exmaple이 m개, 피쳐가 2개라면 ( x1, x2 )
• 학습의 한 싸이클은 아래와 같다. 이걸 많이 돌려서 w, b를 최적화한다.
• (=loss function값이 작아지게 한다.)

--------------------------------
J, dw1, dw2, db <- 초기값 할당

function 한_싸이클_학습() {
  for i=0 -> m
    // loss function 값을 구한다
    z^i = Tranpose(W) * x^i + b
    a^i = Sigmoid(z^i)
    J += Loss(a^i, y^i) // 이거 누적하는 애들은 for문 끝나고 m으로 평균냄 
    // 열심히 미분을 한다.
    dz^i = a^i - y^i 
    dw1 += x1^i * dz^i
    dw2 += x2^i * dz^i
    db += dz^i 

  // 이제 w, b 업데이트 해야되니까, 구한 미분값들 평균 내기
  J /= m
  dw1 /= m
  dw2 /= m
  db /= m

  // 파라미터 w, b 업데이트하기
  w1 -= α * dw1
  w2 -= α * dw2
  b -= α * db
}

Python Vectorization

Neural Network Basics - part 2 of 2

왜함?

명시적인 loop를 줄여야 한다.
연산은 벡터로 하는게 빠르다. 벡터를 쓰자.
numpy built-in function같은걸로 for-loop를 없앨 수 있으면 반드시 없애라.

참고:벡터연산

import numpy as np

u = np.array([1,2,3])
np.random.rand(cnt)
np.exp(v)
np.log(v)
np.abs(v)
np.maximum(v, 0)
u.sum(axis=0)
u.reshape(1,3)

u**2
u/=4

Vectorizing Logistic Regression

피쳐는 $x \in \R^{n_x \times m}$ 매트릭스에 박는다

• $X = \begin{bmatrix}x^1_1 & x^2_1 & ... & x^m_1 \\ x^1_2 & x^2_2 & ... & x^m_2 \\ ... & ... & ... & ... \\ x^1_{n_x} & x^2_{n_x} & ... & x^m_{n_x} \\ \end{bmatrix}$
  • 한 입력의 피쳐 다 쓰면 눈아프다.
  • 대충 $X = \begin{bmatrix} x^1 & x^2 & ... & x^m \end{bmatrix}$ 라고 쓰자.

파라미터도 매트릭스에 박는다.

• $W = \begin{bmatrix} w^1 \\ w^2 \\ ... \\ w^{n_x} \end{bmatrix}$ : $R^{n_x \times 1}$ 열벡터.
• $B = \begin{bmatrix} b & b & ... & b \end{bmatrix}$ : $R^{1 \times m}$ 행벡터

그럼 모든 training example에 대해 $z^i = w^T x^i + b$를 구해보자

• W, X, b가 다 매트릭스니까, 그대로 z값도 매트릭스에 편안히 박는다.
• $Z = W^T X + B = \begin{bmatrix} z^1 & z^2 & ... & z^m \end{bmatrix}$
• 코드로 쓰면 Z = np.dot(w.T, X) + b : b는 dot()결과에 맞춰 알아서 늘어난다. (브로드캐스팅)

모든 training example에 대한 예측치 $a^i = \hat{y}^i$를 구하면

• $A = \sigma(Z) = \begin{bmatrix} a^1 & a^2 & ... & a^m \end{bmatrix}$

Vectorizing Logistic Regression's Gradient Output

dz, dw, db가 모두 매트릭스라고 하자

• $dz = (A-Y)$
• $dw = \frac{1}{m} X\ dz^T$
• $db = \frac{1}{m}$ (np.sum(dz))

Numpy

(m,n) (1,n) --> (1,n)벡터가 복사돼서 (m,n)에 적합하게 바뀜.
연산마다 바뀌는게 좀 다름

(m,n) + R 처럼 숫자를 더하면 그대로 모든 원소에 다 더해버림.

shape 주의

• shape가 (m,)인 경우, 열벡터도 행벡터도 아닌 1-rank array라고 한다.
  • Tranpose하면 달라지는게 없다.
• (m,1)은 컬럼벡터가 맞다. (1,n)은 로우벡터가 맞다.
  • 트랜스포즈하면 쉐이프 바뀐다.
• 1-rank array쓰면 버그나기 쉬우니까 쓰지마라.
  • assert(a.shape == (m,1))처럼 아예 싹을 잘라버려라.

Shallow Neural Networks

뉴럴네트워크가 무엇인가

뉴럴네트워크는 레이어가 여러개다.
레이어는 stacks of units이다.

a (액티베이션) 값과 w, b를 표기할 때, 몇 번(i-th)레이어에 속하는지 superscript bracket으로 표기한다.

• input layer (1st)에 속하는 input vector $X$ = $a^{[0]}$
• hidden layer (2nd)에 속하는 activations, W, b --> $a^{[1]}$, $W^{[1]}$, $b^{[1]}$,
• output layer (3rd)에 속하는 activaion = $a^{[2]} = \hat{y}$

위의 경우는 총 3개 층으로 구성되어있다.

• 인풋레이어 빼고 2개만 세서, 2-layer NN 이라고 부른다.

각 레이어는 모두 액티베이션을 가진다.

• 인풋레이어의 각 인풋피쳐도 액티베이션으로 생각한다. 히든레이어로 값을 패스하는 역할
• 히든레이어는 아웃풋 유닛으로 넘길 값을 계산
• 아웃풋레이어는 최종 값 ($\hat{y}$)을 계산

Computing a NN's Output

로지스틱 회귀의 cost를 계산하는 뉴럴네트워크를 만든다고 하자.

2주차에서 만들었던 로지스틱 회귀 모델은 사실상 레이어가 하나였다.
그러니 W, B도 한 레이어에 대해서만 하나씩 있었고, 시그마 계산도 한 레이어에서 한 번 했다.

아래는 히든 레이어에서 한 번, 아웃풋레이어에서 한 번 --> 도합 두 번을 한다.
= week2에서 한 번 하던걸 그냥 연이어서 두 번 하는거다.

$n_x = 3$, $l$(hidden layer의 unit 개수) = 4 라고 가정하자
그 상태에서 단일 example에 대해, 여러 개의 examples에 대해 각각 NN 아웃풋을 뽑아보자.

m=1인 경우 (training example 하나에 대해서)

W 트랜스포즈는 알아서 했다고 생각을 하자. 그리고 $n_x=3, n^1=4$
$X=A^{[0]}$임.

• $z^{[1]} = W^{[1]}X + b^{[1]}$ : shape는 (4,1) = (4,3)(3,1) + (4,1)
  • 4는 히든레이어 유닛의 개수 $l$. 각 유닛별로 출력 z를 하나씩 뱉음.
• $a^{[1]} = \sigma(z^{[1]})$ : shape는 (4,1) = (4,1)
• $z^{[2]} = W^{[2]}a^{[1]} + b^{[2]}$ : shape는 (1,1) = (1,4)(4,1) + (1,1)
• $a^{[2]} = \sigma(z^{[2]})$ : shape는 (1,1) = (1,1)

m>1인 경우 (training example 여러 개)

W 트랜스포즈는 알아서 했다고 생각을 하자. 그리고 $n_x=3, n^1=4$

• $Z^{[1]} = W^{[1]}X + b^{[1]}$ : shape는 (4,m) = (4,3)(3,m) + (4,m)
• $A^{[1]} = \sigma(Z^{[1]})$ : shape는 (4,m) = (4,m)
• $Z^{[2]} = W^{[2]}A^{[1]} + b^{[2]}$ : shape는 (1,m) = (1,4)(4,m) + (1,m)
• $A^{[2]} = \sigma(Z^{[2]})$ : shape는 (1,m) = (1,m)

헷갈리니까 각 매트릭스를 펼쳐서 살펴보면

• $X = A^{[0]} = \begin{bmatrix} x^{[1](1)}_1 & x^{[1](2)}_1 & ... & x^{[1](m)}_1 \\ x^{[1](1)}_2 & x^{[1](2)}_2 & ... & x^{[1](m)}_2 \\ ... & ... & ... & ... \\ x^{[1](1)}_{n_x} & x^{[1](2)}_{n_x} & ... & x^{[1](m)}_{n_x} \\ \end{bmatrix}$
  • 각 열 : i-th examples
  • 각 행 : i-th exmaple의 features
• $Z^{[1]} = \begin{bmatrix} z^{[1](1)}_1 & z^{[1](2)}_1 & ... & z^{[1](m)}_1 \\ z^{[1](1)}_2 & z^{[1](2)}_2 & ... & z^{[1](m)}_2 \\ ... & ... & ... & ... \\ z^{[1](1)}_{n^1} & z^{[1](2)}_{n^1} & ... & z^{[1](m)}_{n^1} \\ \end{bmatrix}$
  • 각 열 : i-th examples에 대한 z
  • 각 행 : i-th unit (몇 번째 유닛이 뱉은, i-th example의 z임?)

Activation funcions

유명한 활성화 함수는 무엇이 있나

sigmoid, tanh, ReLU, Leaky ReLU

sigmoid에 대해서

• sigmoid는 binary classification할 때 output layer의 활성함수로 주로 사용
• 웬만하면 쓰지마라. 차라리 tanh를 쓰든지, ReLU를 쓰자.
• sigmoid보다는 tanh가 더 낫다. 평균이 0으로 찍혀서 편하고, 범위도 더 넓다.

위에서 살펴본 네 함수는 모두 비선형함수다. (선형함수가 아니니까)

비선형 활성함수가 왜 필요한가?

선형함수는 아쉽게도 태생적으로 선형적이라는, 단순하다는 문제가 있다.

• 선형 활성화 함수 $g(x)=x$를 쓴다면, activation값 a는 $a=g(z)=z$가 된다.
• 선형함수로 뭔짓을 해도 결국 신경망은 언제나 선형함수 결과만 뱉는다.
• 신경망 10억개가 백날 선형값 뱉어봤자, 결국에는 모든 결합은 선형결합이다.
• 히든레이어의 의미가 없다. GPU 먹고 뱉는게 단순한 선형결합이라니.

비선형함수는 선형공간을 벗어나 비선형 공간을 사용한다.

• 신경망이 복잡한 데이터 패턴을 학습할 수 있게 됨
• 비로소 보다 쓸모있는 모델이 탄생

그러나 선형함수가 언제나 쓸모없지는 않다. 특별한 경우 쓸 수도 있다.

• y가 real number인 경우, 아웃풋레이어에 선형 활성화 함수를 사용할 수 있다.
• 그러나 히든레이어에는 비선형함수를 쓰는 것이 좋다.

Derivatives of Activation Functions

가정 : $g(z) = a$

• 가로축은 z
• 세로축은 활성화함수 값 $g(z)=a$

Sigmoid Function
$g(z) = \frac{1}{1 + e^{-z}}\\ g'(z) = g(z) \cdot (1 - g(z))\\ g'(z) = a \cdot (1 - a)$

Tanh Function
$g(z) = \tanh(z) \\ g'(z) = 1 - g(z)^2 \\ g'(z) = 1 - a^2$

ReLU Function
$g(z) = \max(0, z) \\ g'(z) = \begin{cases} 0 & \text{if} z < 0 \\ 1 & \text{if} z > 0 \end{cases}$

Leaky ReLU Function
$g(z) = \max(0.01z, z) \\ g'(z) = \begin{cases} 0.01 & \text{if } z < 0 \\ 1 & \text{if } z > 0 \end{cases}$

Gradient Descent for Neural Networks

1개 히든 레이어를 갖는 뉴럴네트워크에서 gradient descent를 구현한다.

이미 본 대로 파라미터는 아래와 같다

• $W^{[1]}, W^{[2]}, b^{[1]}, b^{[2]}$

Forward, Back Propagation, Gradient Descent를 위한 공식은 아래와 같다.

Forward Propagation
$Z^{[1]} = W^{[1]}X + b^{[1]} \\ A^{[1]} = g^{[1]}(Z^{[1]}) \\ Z^{[2]} = W^{[2]}A^{[1]} + b^{[2]} \\ A^{[2]} = g^{[2]}(Z^{[2]}) \\$

Backpropagation
$dZ^{[2]} = A^{[2]} - Y \\ dW^{[2]} = \frac{1}{m} dZ^{[2]} (A^{[1]})^T \\ db^{[2]} = \frac{1}{m} \sum dZ^{[2]} = \frac{1}{m} \text{np.sum(}dZ^{[2]} \text{,axis=1,keepdims=True)}\\ dZ^{[1]} = ((W^{[2]})^T dZ^{[2]}) ☉ (g'^{[1]}(Z^{[1]})) \text{ --- ☉:element-wise product}\\ dW^{[1]} = \frac{1}{m} dZ^{[1]} X^T \\ db^{[1]} = \frac{1}{m} \sum dZ^{[1]} = \frac{1}{m} \text{np.sum(} dZ^{[1]} \text{, axis=1, keepdims=True)} \\$

Gradient Descent Updates
$W^{[1]} = W^{[1]} - \alpha dW^{[1]} \\ b^{[1]} = b^{[1]} - \alpha db^{[1]} \\ W^{[2]} = W^{[2]} - \alpha dW^{[2]} \\ b^{[2]} = b^{[2]} - \alpha db^{[2]} \\$

Random Initialization

행렬 $W$의 원소를 전부 0으로 초기화 한다면?

• 히든레이어의 모든 유닛이 같은 함수만 계산, 뉴럴네트워크 학습 제대로 안됨
• symmetry breaking problem

그래서 $W$의 원소는 0이 아닌 충분히 작은 값으로 초기화해야 한다.

• np.random.randn(유닛 갯수, 피쳐 갯수) * 0.01
  • 0.01은 작은 값을 만들기 위한 임의의 상수. 뭐든 적절한걸로 넣으면 됨.
• 큰값으로 하면 왜 안됨? : 활성화함수가 포화상태(saturation)가 됨 -> 기울기 작아님 -> 학습 느려짐
  • 함수의 포화 : 입력값이 변해도 함수값이 변하지 않는 것 (양끝 미분값이 0으로 포화)

Deep Neural Networks

Deep L-layer NN

딥 뉴럴 네트워크의 깊이는 모델이 학습가능한 복잡도와 연관있음
그러나 어느정도의 깊이가 문제해결에 적절한지 미리 알 수 없고, 경험적으로 결정해야 함.
Cross Validation Data, Development Set으로 평가.

레이어 노테이션

• $l$(소문자 L) : 레이어 번호 (몇 번째?
• $L$ : 마지막 레이어 번호 (L-layer NN)

일반화된 forward propagation 식

일반화된 식은 ($1 \le l \le L$에 대해서)

• $Z^{[l]} = W^{[l]}A^{[l-1]} + b^{[l]}$
• $A^{[l]} = g^{[l]}(Z^{[l]})$

각 매트릭스의 차원계산을 잘 못하면 인생이 슬퍼질 수 있다.

• $W^{[l]} : (n^{[l]}, n^{[l-1]})$
• $b^{[l]} : (n^{[l]}, 1)$ -- numpy가 알아서 broadcasting
• $Z^{[l]}, A^{[l]} : (n^{[l]}, m)$

back propagation

일반화하면

• $dZ^{[l]} \\ = W^{[l+1]^T} dZ^{[l+1]} * g'^{[l]}(Z^{[l]}) \\ = dA^{[l]}*g'^{[l]}(Z^{[l]})$
• $dW^{[l]} = \frac{1}{m} dZ^{[l]}A^{[l-1]^T}$
• $db^{[l]} = \frac{1}{m} \text{np.sum(} dZ^{[l]} \text{, axis=1, keepdims=True})$
• $dA^{[l-1]} = W^{[l]^T}dZ^{[l]}$

맨 처음과 끝을 살펴보면

• $dZ^{[L]} = A^{[L]} - Y$
• $dZ^{[1]} = W^{[2]^T}dZ^{[2]}*g'^{[1]}(Z^{[1]})$
• $dW^{[1]} \\ = \frac{1}{m} dZ^{[1]} A^{[0]^T} \\ = \frac{1}{m} dZ^{[1]} X^T$
• $db^{[1]} = \frac{1}{m} \text{np.sum(} dZ^{[1]} \text{, axis=1, keepdims=True})$

Why Deep Representation

딥 뉴럴네트워크는 단순한 특징학습에서 시작. 뒷 레이어로 넘어가면서 앞단의 학습내용을 조합하고 더욱 복잡한 내용을 학습. 단계적으로 복잡도를 높이면서 학습.

Hierarchical Feature Learning
= Simple to Complex Representations

• Early Layers : 단순한 특징 학습. 기본적이지만 중요한 것들.
• Intermediate Layers : 단순한 특징을 결함, 더 복잡한 구조 형성
• Deep Layers : 더더더 복잡한 패턴 인식

Circuit Theory : 논리게이트로 계산하는 함수는 shallow NN보다 Deep NN이 더 잘한다.

• Shallow하면 유닛이 지수적으로 늘어나는데, Deep하면 로그수준임.

Building Blocks of DeepNN

이제껏 살펴본대로 딥뉴럴네트워크 구현은 아래 내용을 포함한다.

• Forward Propagation
• Back Propagation + update(Gradient Descent)
• 그리고 위 두 가지의 반복 (Training Iteration)

Forward Propagation

• 입력 : $a^{[l-1]}$
• 출력 : $a^{[l]} = g^{[l]}(z^{[l]})$
  • cache에 $z^{[l]}$값을 저장하고, back propagation때 사용.

Back Propagation + Gradient Descent

• 입력 : $da^{[l]}$
• 출력 : $da^{[l-1]}$
  • cache에 $dW^{[l]}, db^{[l]}$ 뽑아서 저장. 레이어 $l$의 Gradient Descent에 활용

Parameters vs Hyperparameters

(모델) 파라미터 : W, b

하이퍼파라미터 : 사람의 선택이 필요. 학습 알고리즘을 제어하는 파라미터.

• e.g., learning rate $\alpha$, 히든레이어 개수 $L$, 유닛의 수, 활성화 함수 종류
• 하이퍼파라미터는 모델파라미터의 최종 값 결정

하이퍼파라미터는 경험적으로, 직관에 따라 결정한다.
해결하려고 하는 문제, 데이터의 성격, 컴퓨팅 인프라에 따라 최적 하이퍼파라미터가 달라질 수 있음. 따라서 주기적으로 하이퍼파라미터를 재조정하고 모델을 최적화해야 함.

딥러닝의 강점

딥 러닝은 매우 유연하고 복잡한 함수를 학습하는 데 강점 있음
주어진 입력 X에 대해 출력 Y를 예측하는 Supervised Learning에서 매우 효과적

그래서 딥러닝이 뇌와 무슨 관련이 있는가

딱히 없다.