CNN

Foundations of CNN

딥러닝의 발전에 힘입어 컴퓨터 비전도 같이 발전중

주요 응용분야

• Image Classification
• Object Detection
• Neural Style Transfer (e.g., 이미지를 주고 다른 화풍으로 바꾸는 것)

컴퓨터 비전 문제의 어려운 점

• 입력이미지 사이즈가 커지는 것은 차원이 커지는 것
• 차원이 커진다는 것은 신경망 파라미터 개수가 증가한다는 것
• 오버피팅, 연산량, 메모리 문제가 대두됨.
• e.g., 64x64이미지의 너비높이가 두배만 커져도 128x128로 픽셀 수 차이가 2배를 아득히 뛰어넘게 됨.

그래서 Convolution Operation 합성곱 연산이 필요해진다.

• 합성곱 연산은 Convolutional Neural Network 합성곱신경망의 기본 빌딩블록.

합성곱 용어 짚어두기

사실 딥러닝의 합성곱은 다른 학문(신호처리, 수학 등)과는 조금 다르다

• 엄밀하게 다른 학문에서는 합성곱(convolution)에 아래 두 가지 동작을 포함한다.
  • 필터 미러링(뒤집기)
  • 범위 원소단위 곱하기 (cross-correlation 교차상관)
• 미러링을 하면 그쪽 분야에서는 결합법칙 성질을 부여해서 이점을 누릴 수 있다.
• 하지만 딥러닝에선 쓸모가 없다(성능에 영향이 없다). 그러니 할 필요도 없다.

딥러닝에서는 cross-correlation(교차상관)만 필요하다.

• 근데 그냥 이걸 convolution(합성곱)이라고 다들 부른다.
• 그러니 미러링 없이 교차상관만 하는 이 과정을 그냥 합성곱이라고 부르도록 하자.

Edge Detection : 아이디어

이미지의 물체를 인식할 때 가장 먼저 하는 것은 가장자리를 인식하는 것.
가장자리는 cv에서 가장 하위의 특징이다. 가장자리를 본 다음 부분, 전체를 인식한다.

가장자리의 방향은 수직, 수평이 대표적이다.
원한다면 다른 각도의 가장자리도 살펴볼 수 있다. (23도 등)

여기서는 수직 가장자리 검출을 예로 살펴보자.

엣지 디텍션을 하는 기본 아이디어 = 필터(커널)

• 원본 데이터(원본 행렬)과 filter행렬을 convolution 연산
  • 필터는 커널이라고도 한다.
• 새로운 데이터(새로운 행렬)을 구한다.
• 아래 식은 6x6 흑백이미지에 3x3수직필터를 먹여서 새로운 4x4이미지를 만드는 예시.
  • 새로운 이미지는 세로 윤곽선을 표현한다.
  • $*$은 element-wise 곱이 아니라 convolution을 의미한다.
  • 행렬 합성곱 방법

대체 이게 왜 수직윤곽선을 표현한다는거냐?

• 좀 극단적인 예시를 살펴보면 명확하다.
  • 원본 이미지는 왼쪽은 밝은 색, 오른쪽은 검정색이다. 가운데 명확한 세로선이 있다.
  • 수직 필터를 씌워서 4x4 이미지를 뽑았다.
  • 그랬더니 가운데 선이 나왔다. (지금 원본이미지가 작아서 좀 어설픈거지, 원본이미지 사이즈 커지면 납득할만해진다.)
• 지금은 원본이 좌에서 우로 갈수록 어두워지고, 윤곽선 검출 결과도 양수다(30)
  • 만약 원본이 반대로 좌->우 방향으로 밝아진다면, 윤곽선 검출 결과는 음수가 된다 (-30)
  • 즉, 양의 가장자리(positive edge)인지 음의 가장자리인지도 검출이 된다.

참고

• n x n 원본 이미지에
• f x f 필터를 합성곱하면
• (n-f+1) x (n-f+1) 사이즈의 행렬이 나온다.
  • 축소된다.

Edge Detection : 수동 필터

아이디어 부분에서 살펴본 수직 필터는 그냥 필터 선택지 중의 하나다. 다른거 써도 된다.
컴퓨터비전 연구자들이 만들어놓은 필터들이 있다. 아래는 그 예시

• 평범한 수직 필터 : $\begin{bmatrix} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \end{bmatrix}$

• Sobel filter : $\begin{bmatrix} 1 & 0 & -1 \\ 2 & 0 & -2 \\ 1 & 0 & -1 \end{bmatrix}$

• Scharr filter : $\begin{bmatrix} 3 & 0 & -3 \\ 10 & 0 & -10 \\ 3 & 0 & -3 \end{bmatrix}$

수평 방향 엣지를 검출하고 싶으면 수평 방향의 필터를 써야된다.
그냥 수직필터 시계방향90도 회전하면 그게 수평필터다.

• 평범한 수평 필터 : $\begin{bmatrix} 1 & 1 & 1 \\ 0 & 0 & 0 \\ -1 & -1 & -1 \end{bmatrix}$

Edge Detection : 필터 값 학습

근데 연구자들이 이 엣지검출 필터마저 딥러닝으로 구하기 시작했다.
3x3필터의 경우, w값을 9개 놓고 딥러닝 학습을 돌리고, 늘 하던대로 역전파해서 w(필터 값)들을 학습한다.

Padding

입력(원본) 행렬과 필터 행렬을 합성곱하면 축소된 결과 행렬이 나온다.
여기서 문제가 있는데

• 딥러닝은 레이어가 많은데, 레이어를 많이 거칠 수록 이미지가 많이 축소된다.
• 입력 행렬의 중앙에 비해 가장자리는 결과에 적게 반영된다.
  • 합성곱을 할 때 가장자리가 연산에 들어가는 빈도가 적어서 그렇다.

두 가지 문제를 해결하기 위해 입력 주위에 픽셀을 더해 pad한다.
(즉, 원본 이미지 사이즈를 늘린다.)

패딩의 정도 $p$

몇 픽셀을 패딩했는지를 $p$값으로 표현한다.

• 6x6이미지 주위에 1픽셀을 덧대서 8x8로 만들었으면 $p=1$이다.
• 이 경우 필터가 3x3이면 입력 크기와 결과 크기가 같다.
  • 패딩 전 입력 6x6
  • 결과 6x6

합성곱의 두 가지 종류

여기서 입력과 결과의 사이즈가 같냐 아니냐로 컨볼루션의 종류를 두 가지로 나눌 수 있다.

• Valid Convolution : $p=0$
• Same Convolution : $p= (f-1)/2$
  • 패딩을 사용해서 입력이 레이어를 거쳐 축소되어도 본래 사이즈의 결과를 뱉도록 함.

필터의 크기 $f$

보통 필터 행렬의 한쪽 길이 $f$는 홀수로 한다. 그 이유는

• 홀수일 때 입력에 패딩을 대칭으로 줄 수 있다.
• 홀수일 때 필터의 중앙 픽셀을 하나로 정할 수 있고, 위치로 사용할 수 있다.
• 그리고, 그냥 관습이다. 짝수도 성능이 나오긴 하는데, 다들 짝수를 쓰지 않는다.
  • 3x3이 일반적
  • 5x5, 7x7을 쓰기도 한다.
  • 1x1은 특별한 용도가 있다.

Strided Convolution

지금까지는 입력, 필터의 합성곱 연산을 할 때 한 칸씩 이동했다.
여기서 이동을 한 칸이 아니라 그 이상(2칸, 3칸, ...)씩 할 수 있다.
(결과적으로는 결과 행렬의 사이즈가 1칸단위 이동했을 때 보다 축소될 것)

스트라이드 $s$

몇 칸씩 이동하냐를 스트라이드 $s$로 표시한다.
2칸씩 이동하면 $s=2$이다.

패딩, 스트라이드가 적용된 합성곱 결과의 크기

아래를 가정하자

• 입력이미지 크기 nxn
• 필터 크기 fxf
• 패딩 p
• 스트라이드 s

결과 행렬의 한 축 사이즈는

• $\lfloor (n+2p-f)/s \rfloor + 1$
• 내림이 있는 점에 유의

$s$에 따라 이동했는데, 필터가 입력범위를 넘어가면 어떡함?

그래서 거기 계산하지 말라고 한 축 사이즈에 내림했다.

Convolution Over Volumnes (3D합성곱)

지금까지는 2D합성곱을 했다. 즉, 채널이 1개였다.
3D합성곱은 채널이 여러개가 된다.
RGB이미지라면 채널이 3개다($n_C=3$). 특별할건 없다.

• 입력도 3개의 채널을 가진다.
• 한 개의 필터도 3개 채널을 가진다.

사이즈 제약을 살펴보면

• 입력과 필터의 너비,높이가 동일할 필요는 없다. (이제까지 그랬듯)
• 근데 채널 개수 $n_C$ 는 똑같아야 한다.
• ($n_C$를 깊이라고도 부르지만, 헷갈리니까 채널의 수라고 하자.)

필터가 하나일 때

하던대로 하면된다.

• 6x6입력이 R,G,B 3개 있다.
• 3X3필터가 R,G,B 3개 있다.
• 한 위치에 대해 R,G,B 평면 각각 합성곱 값 구한다. (R,G,B별로 3개 결과가 나올 것)
• 구한 3개의 합성곱 값을 더한다. (R+G+B)
• 한 개 필터의 한 위치에 대한 합성곱이 나왔다.
• 그러니 다 하고나면 결과 행렬은 4X4 사이즈. (기존과 같음)

출력의 사이즈는 필터가 하나인 경우(${n^{'}_C} = 1$) 2D합성곱과 똑같다.

• $(\lfloor (n+2p-f)/s \rfloor + 1) \times (\lfloor (n+2p-f)/s \rfloor + 1) \times 1$
• 패딩 스트라이드 없으면 뭐 그냥 $(n-f+1)\times(n-f+1)\times 1$ 이겠지.

결과 행렬의 0행0열 위치의 원소값을 구하는 과정을 자세히 풀어쓰면

• 아래와 같이 입력과 필터가 있다.
  

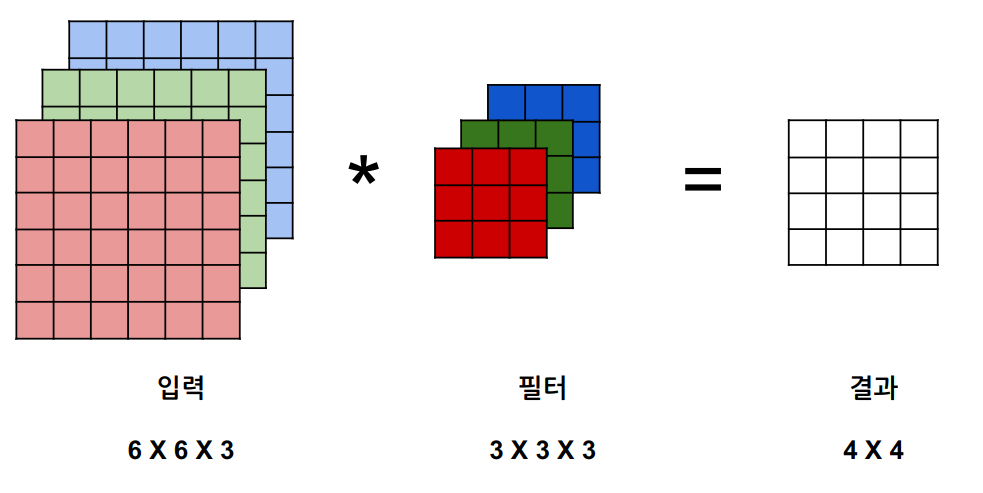
• 각 채널에 대해 합성곱 값을 구한다.
  

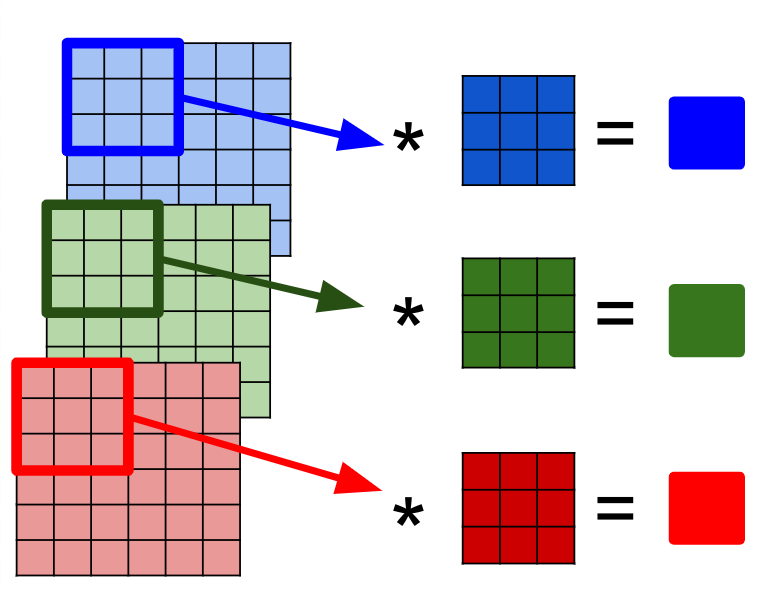
• 채널별로 구한 합성곱 값을 더해서 결과행렬에 넣는다.
  

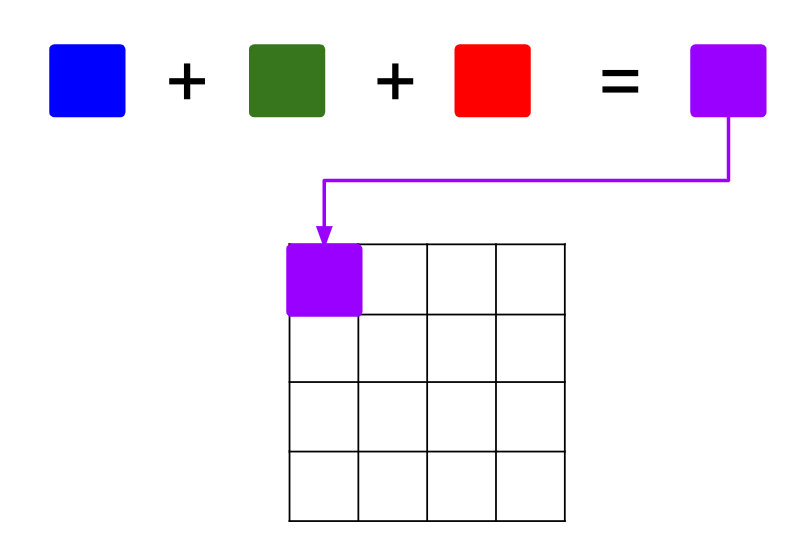
필터가 2개 이상일 때

이거도 그냥 하던대로 하면 되는데, 결과의 평면 개수가 달라질 뿐

필터별로(뽑고자 하는 특징별로) 각각 합성곱 결과 평면 구한다.
그거 그냥 평면 쌓으면 된다. = 위에서 한 짓을 필터 개수만큼 하면 된다.

• 필터가 2개이면 (${n^{'}_C} = 2$), 평면이 2개 나온다.
• 즉, 아래와 같이 가정하자
  • 입력이 6X6X3
  • 3X3X3짜리 필터가 2개
  • 그럼 출력은 4X4X2

Convolution Layer (One layer of a convolutional net)

딥뉴럴 네트워크에 합성곱을 도입하기 위해, 한 레이어가 어떻게 구성되는지 살펴본다.
이 레이어는 CONV(Convolution) 레이어라고 부른다. 합성곱신경망에 이것만 있는건 아닌데, 이것만 있어도 아무튼 되기는 한다.

네트워크상의 $l$번째 레이어에서 볼 때

• 입력되는 이미지는 $a^{[l-1]}$과 같다.
• 현재 레이어의 필터는 $w^{[l]}$와 같다.
• 이미지와 필터의 합성곱은 $z^{[l]}$과 같다.
• 합성곱 bias $b^{[l]}$ 더하고 ReLU같은걸 씌워서 비선형성을 주면 $a^{[l]}$이 된다.
  • 현재 레이어의 출력이자 다음 레이어의 입력

여기서 채널의 개수 $n_C^{[l]}$이 의미하는바가 상당히 헷갈린다.

• 레이어 $l$이 출력하는 채널이 몇 개냐(출력행렬의 채널 개수)를 의미한다.
  • 각 필터가 몇 개 채널을 들고있냐가 아니다.
• 즉, 해당 레이어의 채널 개수는 필터의 개수이다.

각 레이어별 행렬들의 사이즈를 살펴보면

• 입력 : $a^{[l-1]} = n_H^{[l-1]} \times n_W^{[l-1]} \times n_C^{[l-1]}$
• 각각의 필터 : $f^{[l]} \times f^{[l]} \times n_C^{[l-1]}$
• 필터의 모음(Weights) : $w^{[l]} = f^{[l]} \times f^{[l]} \times n_C^{[l-1]} \times n_C^{[l]}$
• bias : $b^{[l]} = 1 \times 1 \times 1 \times n_C^{[l]}$
• 출력(activation) : $a^{[l]} = n_H^{[l]} \times n_W^{[l]} \times n_C^{[l]}$

이걸 여러 레이어로 확장해서 분류기로 만든다면 하게 될 일은

• 이짓을 많이많이 하고
• 마지막 출력층에서
  • a를 flatten하고(하나의 벡터로 만들고)
  • softmax같은데에 입력으로 박아버리면
• 분류기가 된다.

합성곱 신경망 개요 정리하기

특히, 합성곱 신경망을 디자인한다는 것은

• 필터 크기와 개수, 스트라이드, 패딩, 등의 하이퍼파라미터를 결정하는 것.

위에서 살펴본 대로 구현한 합성곱 신경망의 특징을 돌아보면

• 네트워크가 딥해질수록 (레이어를 많이 지날수록)
  • 입력의 크기, 즉 높이와 너비는 줄어든다.
  • 채널은 많아진다.

합성곱 신경망이 갖는 레이어의 종류

• Convolution (CONV) :
  • 지금까지 본게 이거다.
  • 이거만 있어도 되긴 하지만, 보통 Convolutional Network라면 아래 두 레이어도 갖고 있다.
• Pooling (POOL),
• Fully Connected (FC)

Pooling Layer

CONV레이어는 필터를 정의하고, 입력과 필터의 합성곱을 결과로 뱉었다.

POOL레이어에도 필터가 있다 : 입력에 필터를 먹여서 특징을 요약된 결과행렬을 뱉는다.

• CONV레이어나 POOL레이어나 둘 다 작아진 결과행렬을 뱉는다.
  • 그러나 필터로 하는 연산의 종류와 목적이 다르다.
  • CONV의 합성곱은 특징 추출의 특징이 강했다면, pooling은 특징을 날카롭게 요약하는게 주된 목적이다.
• 하이퍼 파라미터로 필터 크기$f$와 스트라이드$s$를 결정해야 한다.
  • 패딩 $p$는 보통 0이다. 요약하는게 목적인데 크기유지를 할일이 없다. (보통은)
• 특징 : 학습할 파라미터 없다. 하이퍼 파라미터 f, s만 정해주면 된다. (fixed function)

Max Pooling

필터 범위 내에서 최대값을 뽑아서 결과로 뱉는다.

(e.g.,)

• 입력은 5x5 : $\begin{bmatrix} 1 & 3 & 2 & 1 & 3 \\ 2 & 9 & 1 & 1 & 5 \\ 3 & 2 & 3 & 2 & 3 \\ 8 & 3 & 5 & 1 & 0 \\ 5 & 6 & 1 & 2 & 9 \\ \end{bmatrix}$

• 풀링 설정은 $f=3, s=1$

• 출력은 3x3 : $\begin{bmatrix} 9 & 9 & 5 \\ 9 & 9 & 5 \\ 8 & 6 & 9 \\ \end{bmatrix}$

Average Pooling

필터 범위를 평균내서 결과로 뱉는다.
이건 특정한 경우에 쓰고, 보통은 맥스 풀링을 더 많이씀.

(e.g.,)

• 입력 4x4 : $\begin{bmatrix} 1 & 3 & 2 & 1 \\ 2 & 9 & 1 & 1 \\ 1 & 4 & 2 & 3 \\ 5 & 6 & 1 & 2 \\ \end{bmatrix}$

• 풀링 설정은 $f=2, s=2$

• 출력 2x2 : $\begin{bmatrix} 3.75 & 1.25 \\ 4 & 2 \\ \end{bmatrix}$

2D말고 3D행렬에 대해 풀링은 어떻게함?

채널별로 하던대로 풀링 하면됨
3차원 입력에 풀링하면 출력도 3차원임

(e.g.,)
입력 : 5x5x2
풀링 설정 : f=3, s=1
출력 : 3x3x2 (채널 수 그대로)

보통 풀링 하이퍼파라미터는 뭐씀?

• f=2, s=2 : 입력 너비 높이를 반으로 줄여서 출력뱉음
• f=3, s=2

CNN에서 레이어 세는 단위

이제껏 conv레이어, pool레이어 각각 레이어라고 하기는 했지만
사실 CNN에서는 레이어를 세는 방법이 두 가지 있다.

• 인접한 conv+pool 레이어 묶어서 한 레이어로 보기
• conv, pool 레이어 각각을 레이어로 보기 (conv, pool 총 2개)

전자의 conv+pool 세트를 한 개 레이어로 보는게 일반적이다. (후자도 가끔 보이긴 한다.)
pool에는 학습할게 없어서 그렇다.

Fully Connected Layer

합성곱신경망의 끝부분에 있는 레이어. 원래 보던 표준 신경망 그거 맞다.
앞뒤 행렬의 원소 사이가 완전히 싹다 연결된 그 레이어다.

첫 번째 FC레이어는 마지막 POOL레이어의 출력을 FLAT한 벡터로 만든다.
이후 FC레이어는 이전 FC레이어 출력의 크기를 줄인 것을 출력으로 뱉는다.

CNN 장점

• Parameter sharing (변수 공유) :
  • e.g., 이미지 모든 픽셀을 파라미터로 쓰는 대신,
  • 필터와 편항b만 파라미터로 삼는다 : $f^2 + 1$개의 파라미터
  • 학습된 필터는 엣지 검출에도, 전체 특징 탐지에도 쓸 수 있다.
• Sparsity of connection (희소 연결)
  • 작은 파라미터 수로 동작할 수 있는 이유.
  • 출력의 각 부분은 입력의 일부분에만 연결(의존)됨
• Translation Invariance (이동 불변성)
  • 특징을 추출해서 학습하는 CNN의 특징상 이미지 내에서 사물의 위치가 바뀌어도 인식하는데 문제없음.

Deep Convolutional Models (1) : Classics

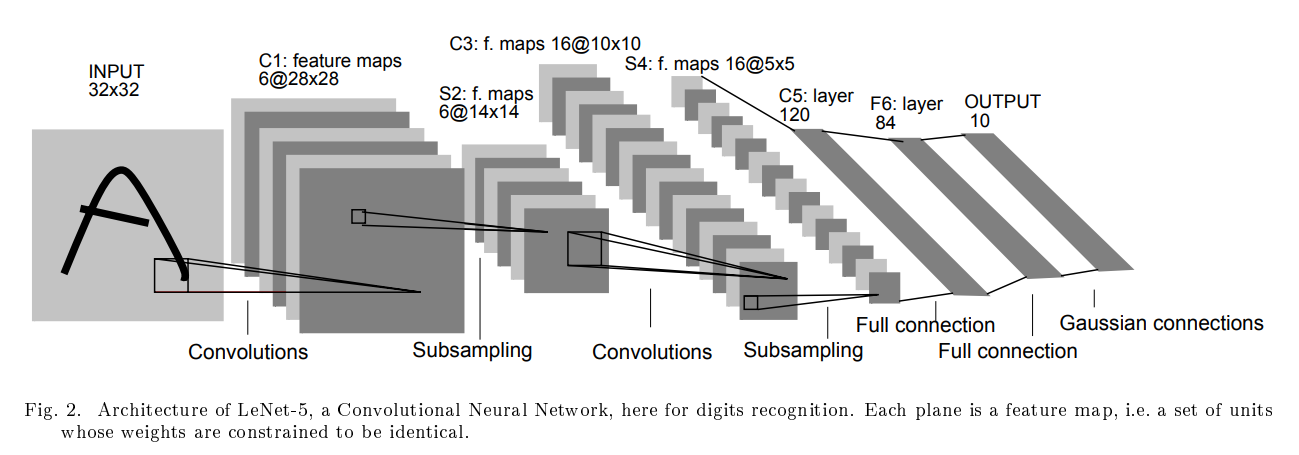
LeNet-5

논문 링크

0~9 숫자 손글씨를 인식하는 모델. 1998년에 나왔음.

• 입력 : 32x32 흑백 손글씨 이미지
• 중간 : CONV + AVG POOL 레이어, FC레이어 나타남.
  • 당시 활성화 함수로 ReLU를 잘 안썼음. 그래서인지 시그모이드, tanh 쓰고 있음.
• 최종 출력 : 10가지 확률 (어떤 숫자일까)
  • 소프트맥스를 안쓴다. RBF(Radial Basis Function)을 쓴다.
  • 현대적으로 해결보려면 소프트맥스 쓰면 된다.

AlexNet

논문 링크

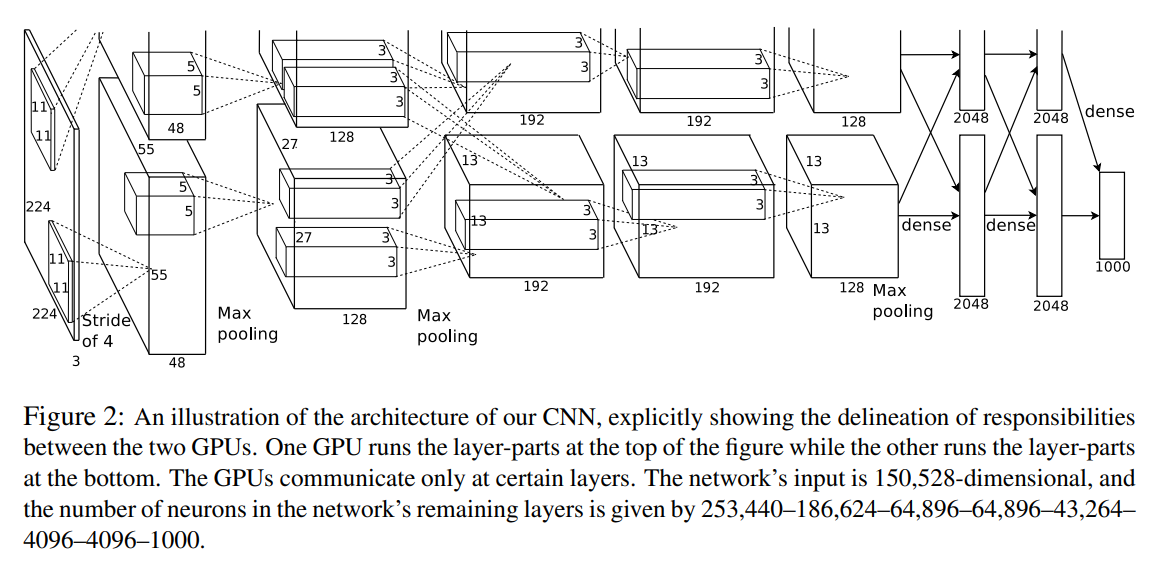
2012년 ImageNet대회 나와서 유명해짐. 이게 나오면서 CV가 뜨기 시작.

• 입력 : 논문에서는 224x224x3 이미지를 받았음.
• 중간 과정 : CONV + MAX POOL, FC
• 출력 : Softmax로 1000개 출력

어떻게 보면 LeNet-5가 더 deep해지고 현대화된 것임.
2012년이면 지금처럼 GPU가 좋지는 못해서 병렬로 학습함.
local response normalization이라는 요즘 잘 안쓰는걸 씀.

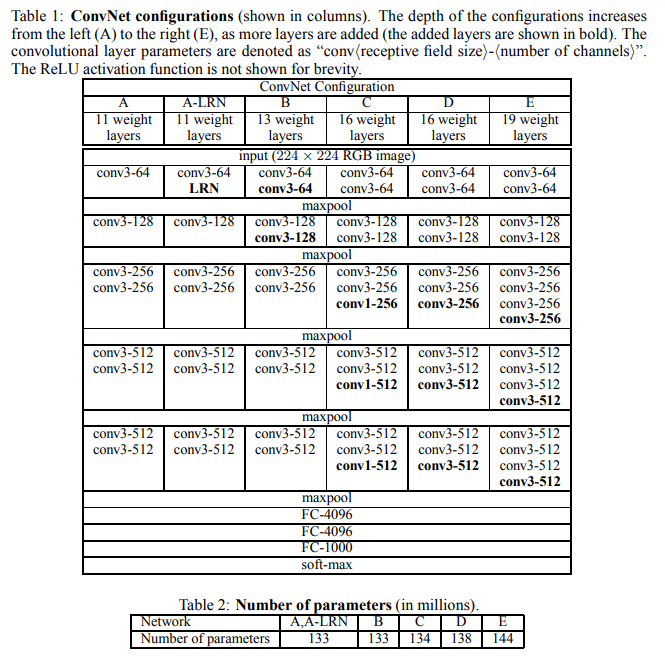
VGGNet (VGG-16)

논문 링크

비교적 단순한 구조로 괜찮은 성능 내는 네트워크로 평가됨. (작다고는 안했다)
많은 하이퍼 파라미터를 갖지 않음.

• s=1, f=3인 same convolution layer
• s=2, f=2은 Max Pooling.

다른 네트워크와 마찬가지로 conv, pool 레이어 번갈아가면서 먹이다가, 최종 출력에 FC-softmax로 결과 냄.

Deep Convolutional Models (2)

ResNet

논문 링크

더 깊은 합성곱신경망을 학습할 수 있도록 하는 네트워크 구조

이론상으로는 신경망이 깊어질수록 (레이어가 많아질 수록) training error가 감소해야 한다. 근데 실제로 해보니까 어느정도 레이어 수 까지는 에러가 감소하다가, 그 수가 더 많아지면 에러가 증가한다. 즉, 신경망의 깊이에 한계를 발견한다. 이 한계를 좀 더 극복하도록 해 깊은 신경망을 학습할 수 있도록 도와주는 네트워크 구조가 ResNet

Residual Network(ResNet)은 Residual Block개념을 사용한다.

• 원래 우리가 만들던 신경망은 Plain Network라고 한다. 이 망이 따르는 기본적인 데이터 흐름을 main path라고 한다.
• Residual Block을 도입한 신경망을 Residual Network라고 한다.
  • 본래 2레이어 뒤의 활성화값을 구하는 식은 $a^{[l+2]}=g(z^{[l+2]})$ 이다.
  • 근데 이거 구할 때 앞전에 있던 활성화값을 끌어와서 더한다. 식을 $a^{[l+2]} = g(z^{[l+2]} + a^{[l]})$로 바꾼다는 말이다. 이짓을 두 레이어 간격으로 한다.
• $a^{[l]}$값을 레이어 $l+2$의 ReLU적용 직전으로 보내는 경로를 shortcut (skip connection)이라고 한다.
  • resnet은 main path뿐 아니라 shortcut을 갖는다.

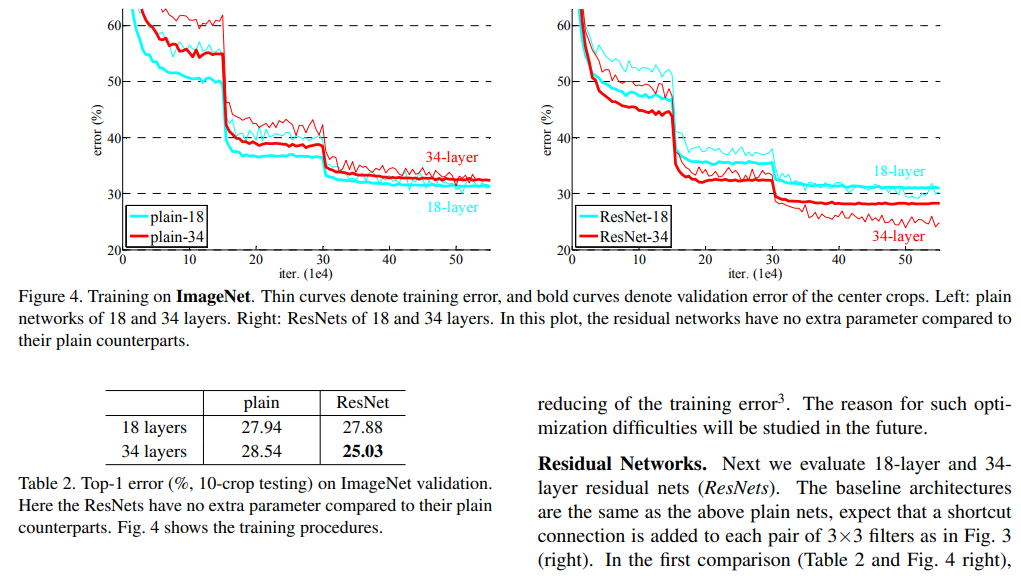
그래서 이거 왜 동작함?

• 보통 신경망 깊이가 증가하면 기울기 소실(vanishing)문제로 성능이 저하된다.
• 여기에 Residual Block을 도입하면 더 깊은 네트워크에서도 identify function(항등함수)을 비교적 잘 학습한다. ReLU같은거.
• 만약 $w^{[l+2]}=0$이 되는 대참사가 발생하면
  • plain net이면 $a^{[l+2]} = g(z^{[l+2]}) = 0$ 이라서 슬퍼지는데
  • ResNet은 $a^{[l+2]} = g(z^{[l+2]} + a^{[l]}) = g(a^{[l]}) = a^{[l]}$가 된다.
• 항등함수니까 성능저하의 우려는 없고, 잘 걸리면 성능 향상도 노려볼 수 있는 것.

보통은 same convolution을 해서 차원을 유지시키고, Res block내에서 $a^{[l]}$을 더할 수 있도록 해줌.
차원이 달라지면 새로운 매트릭스 $W_s$를 끼워준다. (파라미터일 수도, 그냥 차원 맞춰주기 위한 패딩 역할일수도)

1x1 Convolutions

언뜻 보면 그냥 행렬 각 원소에 숫자 하나 곱해주는거라 쓸데없어보임.
채널이 하나면 맞는 소린데, 채널이 많아지면 이야기가 달라진다.

6x6x32에 1x1x32필터로 합성곱하면, 이는 32개 입력 받아서 한 출력 내는거라고 볼 수 있음.
= 6x6행렬을 필터 개수만큼 결과로 뱉기

• 채널 수 너무 많을 때 줄일 수 있음 (풀링은 채널 개수 못바꿈)
• shape안바꾸면서 비선형성을 더해줄 수 있음
• network in network라고도 함. (필터의 채널개수만큼 입력받아서 1개 결과 뱉으니까)

Inception Network

논문 링크

구글에서 만든거라 구글넷이라고도 불림.

CNN 설계할 때 어려운 점이 필터 크기 정하기, 폴링층 쓸지 결정하기임.
Inception Net은 그냥 다함. 아키텍쳐가 복잡해지지만 성능은 아무튼 괜찮아진다.

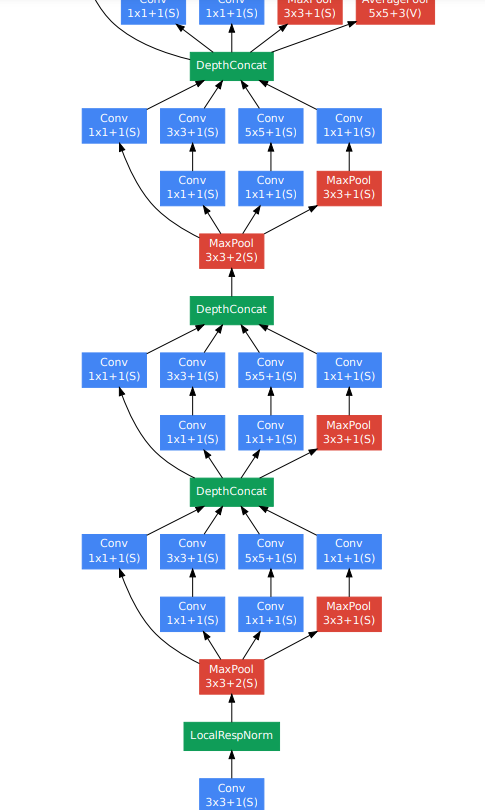
인셉션 모듈

• 1x1, 3x3, 5x5 same convolution filters (conv layers), pooling layers 모두 적용

• 적용한 결과 모두 쌓아서 최종 출력으로 연결. (인셉션 모듈을 쌓는다고 한다)

• 문제 : 계산비용 너무 크다. 데이터 규모 커지면 문제가 크게 드러남.

  • 해결(비용 절감) : bottleneck 레이어 사용 (1x1합성곱을 사용해 채널 수 줄이는 레이어).
  • 근데 채널 수 적당히 줄여야 된다. 너무 과도하게 줄이면 성능 작살난다.

사이드 브랜치

• 네트워크 중간에서 나오는 출력으로 예측, 오버피팅 방지.

아래 그림에서 반복되는 단위를 인셉션 블록이라고 한다.

MobileNet

경량화된 딥러닝 모델. 주로 모바일이나 임베디드 시스템에서 잘 돌아가게 설계됨.
Depthwise Separable Convolution기법으로 계산비용 절감.

v1

키 아이디어 : 원래 하던 표준 합성곱연산을 DSC로 대체.
DSC의 과정은 크게 2스텝

• depthwise convolution : 채널별로 독립적으로 합성곱 수행.
• pointwise convolution : 1x1합성곱해서 여러채널의 출력 결합. (+채널간 상호작용 학습)

v2

v1에 두 가지 도입

• residual connection 도입
• bottleneck block구조 조입
  • 입력채널 수 확장 (복잡한 구조 학습 위해)
  • depthwise convolution
  • projection (~pointwise convolution)

EfficientNet

컴퓨팅 자원에 맞게 신경망 크기를 조정할 수 있도록 설계된 모델.

조절하는 대상

• R : 입력이미지 해상도
• D : 깊이 (레이어 수)
• W : 레이어의 유닛 수 (너비)

세 가지를 각각 직접 조정하지는 않고 Compound Scaling으로 동시에 적절한 비율로 조정.
(주어진 자원으로 가능한 높은 성능 내도록)

결과적으로 이피션트넷의 목표는

• 자원 많으면 더 높은 정확도를 제공하는 것.
• 자원 적으면 더 빠른 속도를 제공하는 것.

오픈소스 쓰기

이미 똑똑한사람들이 좋은거 많이 만들어놨다. 검증 된것도 많다.
모델을 처음부터 구현하기보다는 이미 검증된 코드를 가져와서 비용을 절감하자.

사전학습된 오픈소스 모델을 활용하면 전이학습 쉽게 할 수 있음.
특히 비전 애플리케이션에서 유용함.

오픈소스 커뮤니티를 적극 활용하자.

Data Augmentation

데이터 증강을 통해 가상의 데이터를 생성하면 학습거리가 많아지니까 모델 성능에도 도움이 될 수 있다.

일반적인 증강 기법

• Mirroring
• Random Cropping
• Ratation
• Shearing
• Local Warping
• Color Shifting : RGB값 조정
  • PCA Color Augmentation : PCA(주성분분석)으로 주된 색상을 알아내고, 거기에 해당하는 RGB값을 바꾸는 것 (E.G., 보라색이면 RB값을 바꾸고 G값은 놔두기)

데이터 규모가 작으면 미리 다 증강해서 저장해놔도 된다.
근데 디스크 크기는 한정적이니까, 데이터 불러올 때 실시간으로 증강해서 써도 된다.

State of CV

비전 분야의 문제는 복잡도 대비 데이터의 양이 적다.
그래서 적은 데이터(e.g., labeled data)를 극복하기 위해 hand engienering(직접설계)에 좀 더 의존하게 된다. --> 복잡한 네트워크 구조 발달

데이터가 적은 경우 transfer learning 전이 학습이 특히 유용하다.
cv가 전이학습을 좋아하는 이유임. 데이터가 부족한 상황도 보전하고, 비용도 줄이고.
(그리고 한 모델이 가진 능력이 다른 문제 푸는데에도 보통 도움되는 경우가 많다)

벤치마크와 현실의 비용 사이에서 줄타기도 잘 해야한다.
앙상블기법이 점수는 좋게 나오겠지만, 이걸로 프로덕션 서비스를 하기에는 너무 비싸다.

Object detection : Bounding Box

Object Localization

Object Detection은 이미지 내 존재하는 여러 사물들의 클래스와 위치를 찾는다.
이에 선행돼야 할 것이 이미지 분류와 Object Localization이다.

• 로컬라이제이션은 이미지 내에서 주로 1개의 오브젝트를 식별해
• 클래스를 지정하고 바운딩박스를 그린다.

어떻게 입출력을 할까 생각해보면

• 입력 x는 이미지다.
• 신경망은 합성곱신경망으로 구성할 수 있다.
• 출력은 두 가지가 나와야겠다.
  • 얘 클래스 뭐임?
  • 애 바운딩박스 어떻게 그릴 수 있음?

출력이 어떻게 나와야 할까를 자세히 생각해보면, 아래처럼 나올 수 있다.

• 클래스는 $c_1, c_2, c_3$ 3개가 있다고 가정하자. 원핫인코딩을 하자. (셋 중 하나까지만 1 가능, 나머지는 0)
• 만약 3개 클래스에 속하는 오브젝트가 검출되지 않으면 $p_c$외의 값은 Don't Care로 간주한다.

출력의 형식에 따라 loss function을 설계해보면 (오차제곱으로 대충)

• $p_c = 1$일 때 : $\mathcal{L}(\hat{y}, y) = \sum^8_{i=1} (\hat{y}_i - y_i)^2$
• $p_c = 0$일 때 : $\mathcal{L}(\hat{y}, y) = (\hat{y}_1 - y_1)^2 = (\hat{p_c} - p_c)^2$
  • 왜요 : 그것이 Don't care니까.
    

Landmark Detection

특징점을 찾고자 할 때, 신경망의 마지막 레이어가 무엇을 뱉어야 할까
우리는 이미지에서 특징점의 x, y 좌표를 찾는다.

• 하나의 특징점을 찾고싶다.
  • 일단 그 특징점을 갖고 있을만한 대상이 있는지 여부를 결과로 뱉는다.
    • '눈꼬리' 위치를 찾고싶은데, 일단 사람 얼굴이 있기는 하냐?
  • 신경망의 마지막 층이 x, y 두 개 좌표도 뱉는다.
• 찾고싶은 특징점이 4개면 어떡함?
  • 그럼 x, y 4세트 뱉으면 된다.
• 4개가 아니라 엄청나게 많아지면 어떻게됨?
  • 그럼 엄청나게 많은 x,y 세트 뱉으면 된다
  • 점이 많이 모였으니 윤곽선, 자세같은 상위 특징을 검출할 수도 있겠다.
  • 근데 그 많은 점 라벨링된 데이터가 필요하다는걸 잘 생각해야된다.

실제로 몇 개의 네트워크 출력이 나올까 대충 계산해보면

• 2d 사진에서 사람 얼굴위에 있는 64개 점의 (x,y)좌표를 찾고 싶다면
• 최소 1 + 64 x 2개 출력이 나와야 한다.
  $y = \begin{bmatrix} p_c \\ l_{1x} \\ l_{1y} \\ ... \\ l_{64x} \\ l_{64y} \end{bmatrix} = \begin{bmatrix} 얼굴\ 있음? \\ 1번\ 점\ x좌표 \\ 1번\ 점 \ y좌표 \\ ... \\ 64번\ 점\ x좌표 \\ 64번\ 점 \ y좌표 \end{bmatrix}$

Sliding windows detection 알고리즘

윈도우(사각형)으로 이미지의 부분을 일정 간격으로 crop해서 convnet에 입력해서 클래스 도출.
작은 윈도우로 이미지 모든 부분 다 입력했으면, 그 다음은 더 큰 윈도우로 같은 작업 반복함.

단점 :

• 계산비용 비쌈. 실시간탐지에 적합하지 않을 수 있음. (이동간격이나 윈도우 크기가 작을수록 비쌈)
• 윈도우 크기, 이동간격 잘못 정하면 정확도 박살남

그래서 어떡함

• 비싸니까 안비싸게 만들어야지
• 합성곱으로 구현하자 = 윈도우 계산 시퀀셜하게 하지 말고 한방에 빵 끝내버리자 (마치 딥러닝 구현할 때 Vetorization 하는 것 처럼)

Convolutional implementation of sliding windows

그냥 이미지 크롭하지 말고 통째로 convnet 입력으로 넣어버리는거다.
FC부분이 바뀐다. FC레이어를 합성곱으로 구현한다.

• 기존의 FC는 벡터를 출력했다
• 바뀐 FC는 입력(POOL의 출력)에 필터를 적용한다
  • 사실상 FC가 아니라 CONV레이어가 된거다.
  • 바뀐 FC의 출력은 여러 윈도우의 계산 결과다.
  • 즉, 합성곱을 통해 여러 윈도우의 계산을 한방에 처리해버린다. (본래의 슬라이딩 윈도우 알고리즘은 윈도우별로 각각 했지만)
  • 한 방에 하니까 덜 비싸졌다.
• 사실 새로운건 없다. 그냥 FC가 사실상 CONV로 대체된 것이고(여전히 FC로 부르지만), 출력하는 행렬이 여러 연산의 결과를 함께 담고 있는 것 뿐이다.

하지만 여전히 오브젝트의 아주 정확한 영역(위치)을 잡지는 못한다.

• position도 틀렸을뿐더러 width, height도 정확하게 잡을 수가 없다.
• 당연하다. 그냥 슬라이딩 윈도우 과정을 돌린거지, 특정 객체의 영역을 잡은게 아니기 때문이다.
• 똑같은 사이즈의 윈도우를 똑같은 스트라이드로 들이댔는데 정확한 영역을 잡을리가 없다.

그러니 개선을 해야한다

Bounding Box Prediction (YOLO 개요)

슬라이딩 윈도우를 좀 더 정확한 영역의 바운딩박스로 만들기 위해 YOLO 알고리즘을 사용할 수 있다.

YOLO의 주요 아이디어는

• 이미지를 그리드 셀로 나눈다. 각 그리드 셀이 자신의 구역에 있는 객체를 찾게 한다.
  • 객체가 셀 내에 없거나 1개만 있을 때 잘 동작한다.
  • 2개 이상인 경우는 지금 고려하지 않는다.
• 각 그리드 셀마다 classification, localization 알고리즘을 적용한다.
• 각 그리드 셀은 벡터를 출력한다.
  • $p_c, b_x, b_y, b_h, b_w$
  • 각 클래스에 해당하는지 여부 $c_1, c_2, ...$
• 결과적으로 각 그리드 셀은 셀 내의 상대적인 좌표로 표현한 바운딩박스를 예측결과로 뱉는다.
  • $b_x, b_y$은 셀 내에서의 해당 오브젝트의 중심 좌표. 0~1사이의 값. (셀의 가장 큰 좌표가 1)
  • $b_h, b_w$은 셀 내에서의 해당 오브젝트의 크기. (셀의 사이즈가 1)
    • 이거 1보다 커질 수도 있다. 여러 셀에 걸쳐있는 오브젝트인 경우라면.
• 그리드 셀의 개수가 많아질 수록(그리드가 미세해질수록) 객체를 탐지할 확률이 높아진다.

그러나 sliding window와 마찬가지로 한 객체를 여러번 탐지하고, 여러개의 바운딩박스를 그리는 문제가 발생할 수 있다.
각 그리드셀은 각자 자신이 이 물체를 갖고있다고 생각하기 때문이다. 실은 여러 셀에 걸쳐있는데도 말이다.

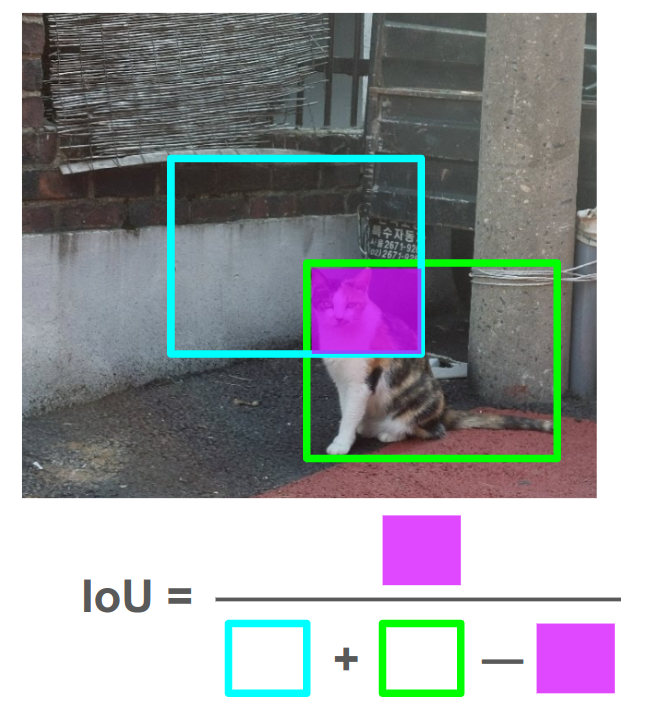
IoU (Intersection over Union)

합집합 위의 교집합

바운딩박스 잘 생성(예측)했나 평가하는 기준

그냥 정답 바운딩박스와 예측 바운딩박스가 얼마나 겹치냐를 나타내는 척도다.
보통 IoU값이 0.5이상이면 잘 예측했다고 한다. 원하면 더 엄격하게 기준을 잡아도 된다.

Non-max Suppression

sliding window, yolo에 대해 살펴본 결과 알고리즘이 한 오브젝트를 여러 번 탐지하는 문제가 있었다.
비-최대값 억제는 알고리즘이 각 오브젝트를 한 번씩만 탐지하도록 함. (중복탐지하지 않고)

여러개 검출된 상황을 정리해서 하나의 검출(바운딩박스)만 남긴다.
두 가지 스텝으로 구성되어있다.

1. 임계값 미만의 확률을 가진 박스를 전부 제거한다. (e.g., $p_c \le 0.6$)
2. 살아남은 박스들에 대해 아래 과정 반복
   2-1) 어떤 영역에서 감지 확률이 가장 높은 박스 하나를 고른다. (최대값 고르기)
   2-2) 그 박스와의 IoU가 높은 박스들을 제거한다. (=비-최대값 억제) (e.g., IoU $\ge 0.5$)

Anchor Box

YOLO 그리드 셀에서 2개 이상의 서로다른 클래스의 객체가 나올 때
모든 객체를 탐지할 수 있는 방법

핵심 아이디어는

• 각 클래스가 가질법한 모양새의 박스를 미리 정의한다. (가로로 길다거나, 세로로 길다거나)
• 출력벡터가 앵커박스 개수 만큼의 $p_c, b_x, b_y, b_w, b_h, c_1, c_2, ...$ 항목을 갖도록 한다.
  • 클래스에 대해 정의된 앵커박스가 2개면 저 항목세트를 2번 출력벡터에 포함시킨다.

• 이제 한 그리드 셀에서 객체 탐지되면, 가장 적합한 앵커박스에 해당 객체를 할당한다.
• 결국 객체는 이제 (그리드 셀, 앵커박스) 쌍에 할당되는 것으로 생각할 수 있다.

그러나 문제가 있는데

• 앵커박스가 n개 정의돼있는데, 셀 안에 n+1개 객체가 탐지되면? : 딱히 해결법없음. 고려대상아님.
• 셀 안에서 특정 1개 앵커박스에 맞는 객체만 여러개 탐지되면? : 딱히 해결법없음. 고려대상 아님. 앵커박스 알고리즘이 아니라 데이터세트에서 승부결정방식을 잘 정해서 해결봐야됨.

YOLO

는 최첨단기술이 결합된 아주좋은 알고리즘이다. 그냥 갖다쓰면 된다.

1. YOLO형식에 맞게 라벨링된 데이터 준비해서
2. 예측(객체탐지)해서 바운딩박스 그리고 (!! 탐지된거 없으면 $p_c = 0$, 나머지 값들 don't care)
3. 진짜로 객체 있을 확률이 낮은 박스 죽이고
4. non-max suppression으로 한 객체에 한 개 박스 남기기.

Region Proposal (R-CNN)

객체가 없을법한 영역임에도 분류, 탐지 알고리즘을 돌리는건 낭비임
그러니 sliding window를 적용할(classifier를 돌릴) 지역을 한정함.

Segmentation으로 객체가 있을법한 2000개 정도의 영역을 선택하고, 거기에만 우리가 여지껏 해온 convnet알고리즘을 돌린다.

근데 R-CNN은 좀 느렸고, Fast R-CNN, Faster R-CNN으로 점차 개선했음.
하지만 여전히 YOLO보다 느리다. 아직까지는 계산을 일괄로 한번에 때려버리는게 빠르다.

어쨌든 흥미로운 접근방법임.

Semantic Segmentation (U-Net)

논문 링크

개요

Object Detection(Localization)에서는 어떤 객체가 있는 박스범위를 잡고 클래스를 분류했다.

시멘틱 세그멘테이션은 객체의 범위를 픽셀단위로 잡는다.
단순하게 생각하면

• 입력은 이미지
• 출력은 전체 이미지의 픽셀을 클래스분류로 매핑한 것이 된다.

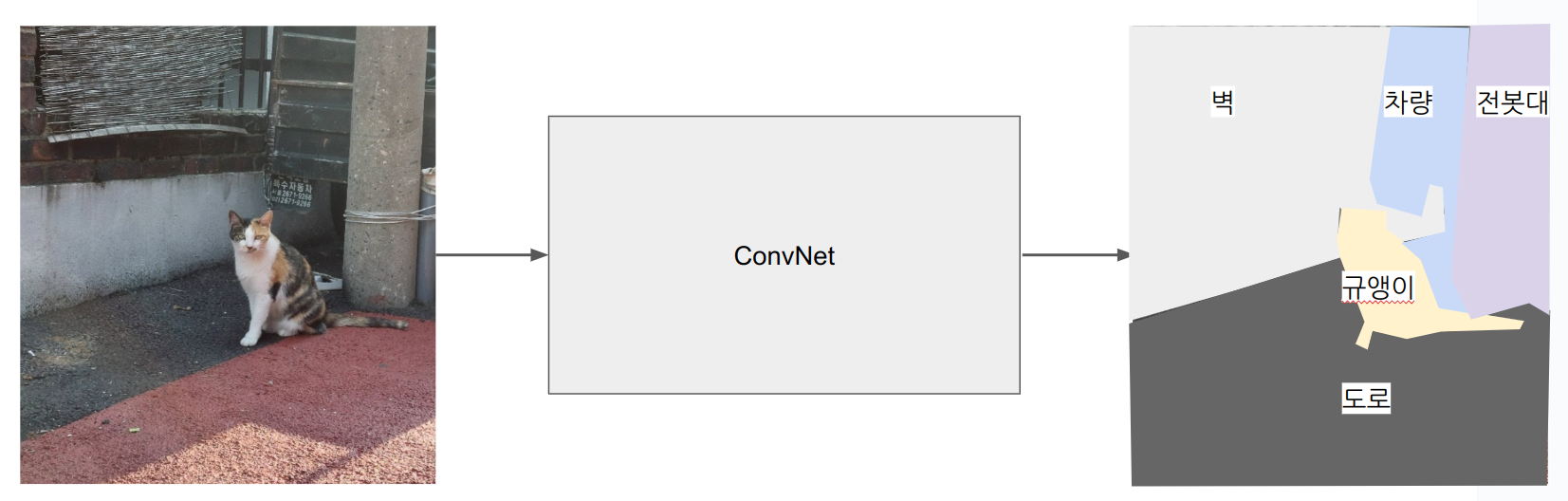
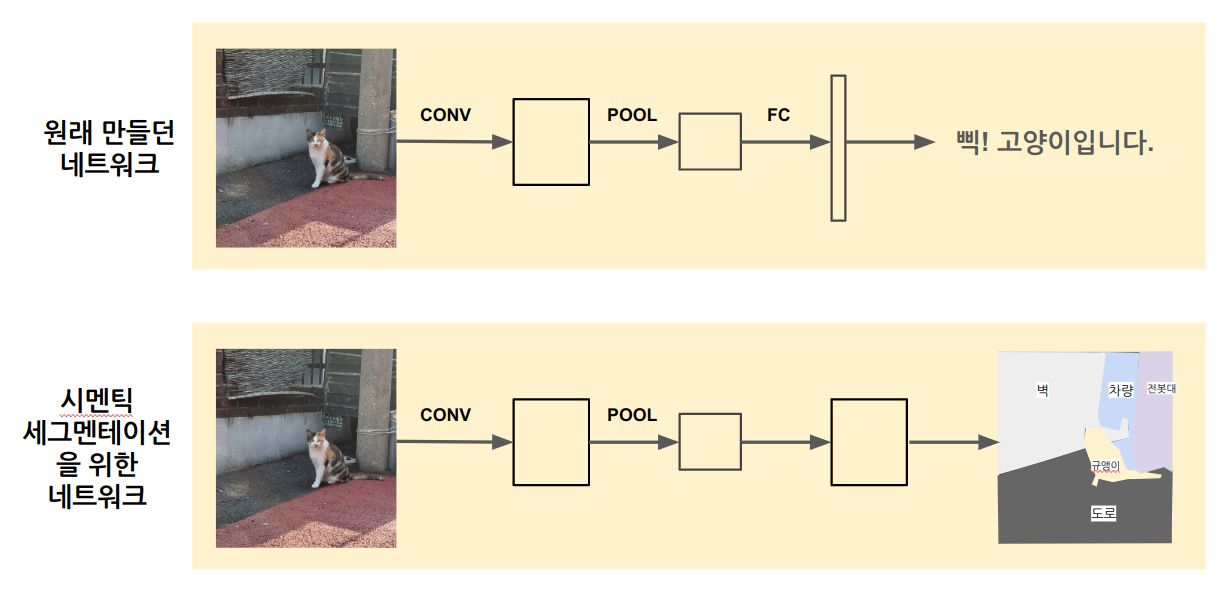
출력이 전체 이미지의 각 픽셀을 설명해야 하기 때문에, 기존 object detection을 위한 네트워크를 좀 수정해야된다.

• 기존 네트워크는 레이어를 지날수록 행렬 사이즈가 줄고 그대로 끝났다.
• 시멘틱 세그멘테이션은 다시 행렬이 커지는 과정이 있어야 한다.
  • 다시 커지는 과정에 Tranpose Convolution 연산을 사용한다.
  • 이 연산은 u-net 아키텍쳐의 핵심 개념이다.

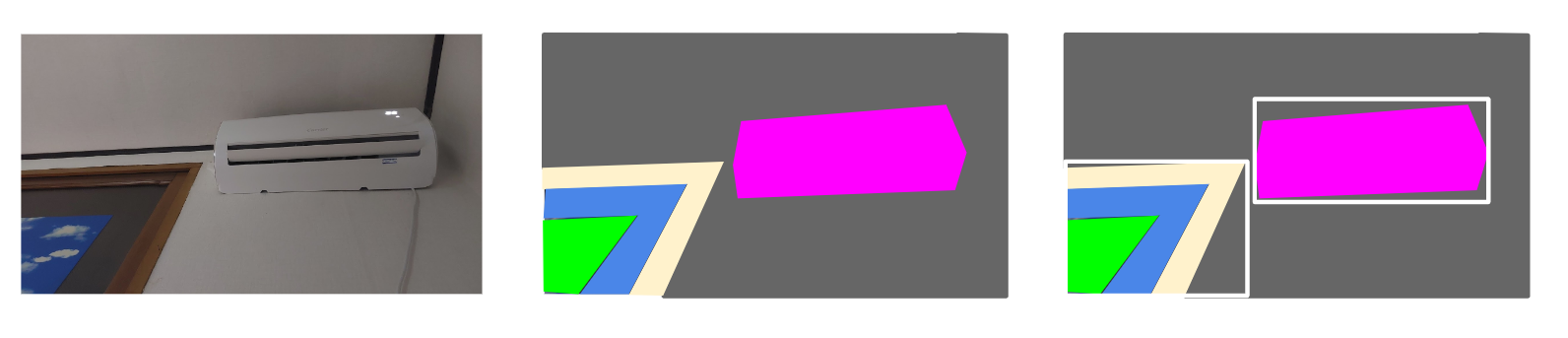
Transpose Convolution

원래 하던 Regular Convolution은

• 입력이 필터보다 크다.
• 필터를 입력위에 대고 곱했다.

Transpose Convolution은 반대다.

• 입력이 필터보다 작다
• 입력을 출력 위에 대고 필터를 곱한다.
• 계산방법 참고

U-Net 아키텍처

앞부분에서 입력에 필터를 먹여서 특징을 추출했다
= 고수준의 컨텍스트를 획득했다.

그러나 특정 픽셀이 어떤 색이었는지에 대한 정보는 잃었다.
잃어버린 정보를 숏컷으로 전달해 보전해준다.

따라서 이 네트워크 구조는

• 고수준의 특징을 가지는 동시에
• 공간정보도 복원한다.

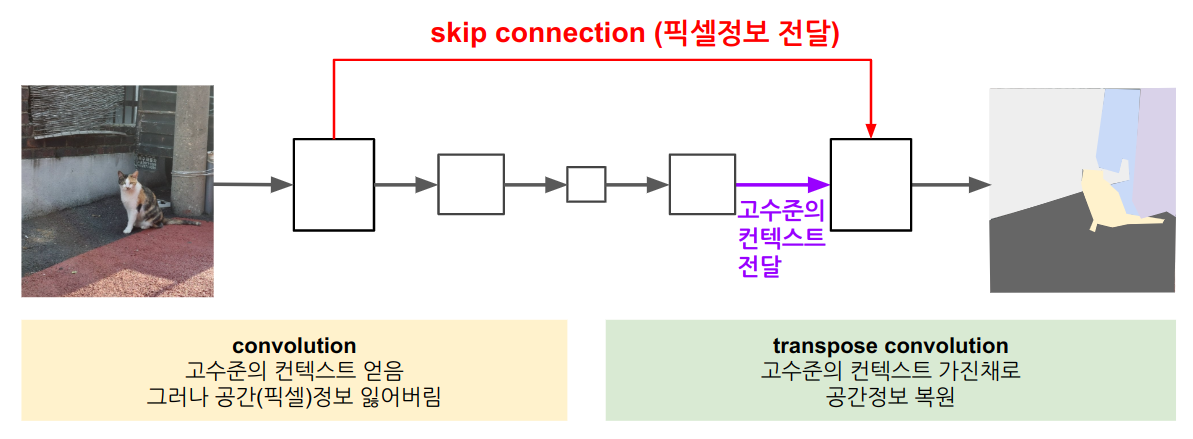
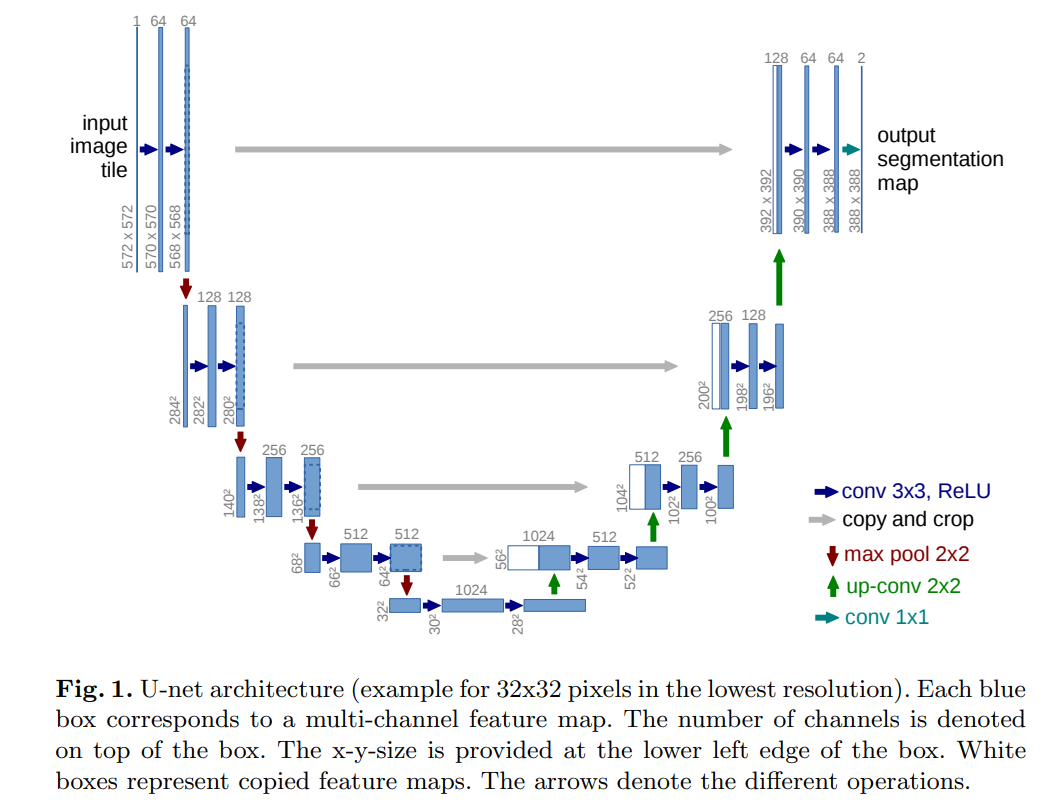
논문의 피겨를 살펴보면 U모양으로 생겼는데, 그래서 U-Net이다.
동작 과정을 대충 살펴보면

• 입력은 h, w, 3의 rgb이미지
• 축소과정 (다운샘플링)
• 확장과정 (업샘플링) + skip connections
• 1x1 convolution으로 각 픽셀의 클래스 확률 계산
• 최종 출력 (h, w, 클래스 수) 의 사이즈.

Face Recognition

개요

얼굴인식에는 두 가지 과제가 있다. 검증보다 인식이 보통 어렵다.

• Face Verification (검증) : 이미지의 얼굴이 '이 사람이 맞냐'를 확인하는 것.
  • 1:1문제
• Face Recognition (인식) : 이미지의 얼굴이 DB목록 중 어떤 사람인지 찾는 것.
  • 1:K문제 --> 작은 오류율이 K가 커질수록 큰 영향을 가짐.

얼굴 검증 시스템 개발이 어려운 이유는 One-shot leanring문제 때문.

One-shot Learning 문제

주어진 사진 한 장으로 사람을 인식할 수 있어야 하는 상황.
보통의 ConvNet-Softmax 네트워크에 사진 하나를 입력하면 그 사람을 알아볼 확률이 낮다.
데이터가 딱 하나밖에 없으니까 당연하다.

그래서 Similarity function $d($img1, img2$)$를 학습한다.
유사도 함수는 두 이미지 간의 유사도를 계산한다.

• d(img1, img2) $\le \tau$ : 같은 사람이다.
• d(img1, img2) $\gt \tau$ : 다른 사람이다

Siamese Network

이미지를 합성곱신경망에 넣고 벡터까지 뽑았다.
가장 마지막의 벡터를 소프트맥스에 넣으면 분류기가 된다.
여기서는 그러지 않는다. 마지막의 벡터를 여러개의 숫자로 인코딩된 사진(입력x)으로 간주한다.

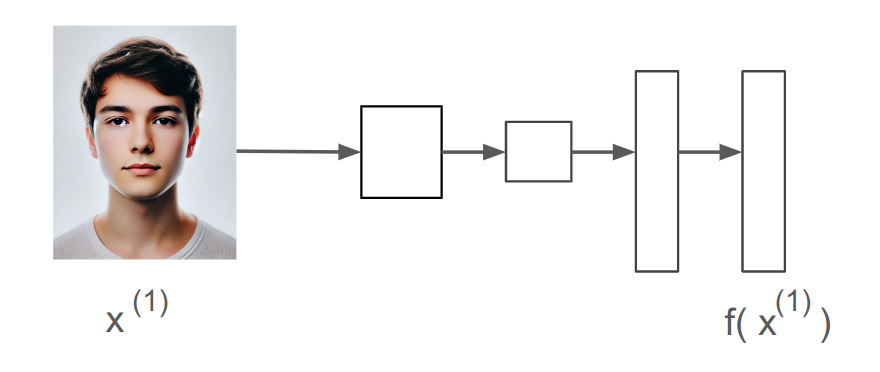
그리고 $f(x^{(i)})$를 유사도 함수 $d()$에 넣어 값을 비교한다.
아래와 같이 직관적으로 표현할 수 있고, 이 동작이 나오도록 하는 것이 신경망 학습의 목표가 되겠다.

• $|| f(x^{(i)}) - f(x^{(j)}) ||^2$ 가 작다면 : $f(x^{(i)}), f(x^{(j)})가 같은 사람
• $|| f(x^{(i)}) - f(x^{(j)}) ||^2$ 가 크다면 : $f(x^{(i)}), f(x^{(j)})가 다른 사람

여기서 각 레이어의 파라미터가 다양해지도록 학습을 잘 시켜줘야 한다.
여기에 Objective Function 목적함수라는 개념을 사용한다.
손실함수로는 Triplet Loss Function을 사용한다.

Triplet Loss

얼굴이미지의 좋은 인코딩을 얻기 위한 파라미터 학습은 Trplet 손실함수로 가능.

왜 삼중항 손실함수라는 이름임?

세 개의 데이터를 같이 보기 때문.

하나의 Anchor 이미지를 놓고 (A)

• Positive 이미지 (같은사람, P)과의 거리를 구함
• Negative 이미지 (다른사람, N)과의 거리를 구함

원하는 것은 아래와 같이 A와P의 거리보다 A와N의 거리가 큰 식을 세우는 것.

• $d(A, P) \le d(A, N)$

그런데 값이 비슷하면 별 의미가 없으니까 margin값 $\alpha$를 준다.

• $|| f(A) - f(P) ||^2 - || f(A) - f(N) ||^2 + \alpha \le 0$

불가능한 자명한 값을 피하면서 손실, 비용함수를 세우면

• $L(A, P, N) = \max(0, d(A, P) - d(A, N) + \alpha)$
• $J = \sum^m_{i=0} L(A^{(i)}, P^{(i)}, N^{(i)})$

학습할 때에는 한 사람에 대한 여러 장의 이미지가 필요하지만,
학습하고 나면 One-shot learning문제를 풀 수 있다. (한명당 한 사진만 주면 잘 인식)

A P N 쌍을 어떻게 고르나

무작위로 고르면 아래 식을 만족하기가 너무 쉬워진다. 왜나면 당연히 A는 P보다는 N과 거리가 멀 것이기 때문.

• $d(A, P) + \alpha \le d(A, N)$
• 그래서 학습하기 어려운 triplet조합을 골라줘야 한다.

학습하기 어려운 조합이 뭐냐?

• A와P의 거리, A와N의 거리가 가까운 경우.
• 그래야 마진값이 적절히 잘 형성된다.
• 쉬운 조합을 고르면 경사하강법이 제대로 동작하지 않고, 학습도 제대로 되지 않는다.
• 어려운 것을 고르면 경사하강법이 AP, AN의 거리를 멀리 떨어뜨리기 위해 적절한 학습을 한다.

Binary Classification으로 Face Verification문제 풀기

트리플렛 손실함수로 샴신경망을 푸는 방법을 살펴봤다.

사실 이진분류로도 해봄직 하다

• 인코딩(임베딩) 계산
• 절대값 차이 계산
• 로지스틱 회귀 수행
• 시그모이드로 최종 예측 출력

이 경우 입력은 2개의 이미지 쌍이 된다.

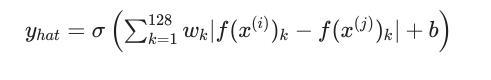
그래서 결국

어째됐든 적절한 파라미터를 학습한 모델을 뽑은 다음
현실세계에서 잘 작동하기 위한 임계값을 잘 정해서 서비스를 시작하면 된다.

Neural Style Transfer

Content(C)와 Style(S)을 조합해 새로운 컨텐츠 Generated Content(G)를 만든다.
신경망의 얕은층과 깊은층에서 추출된 피쳐들을 살펴봐야 한다. (무엇을 추출하는지)

What are Deep ConvNets learning

얕은(낮은 숫자의) 레이어는 간단한 특징을 학습한다. e.g., egde, color
점점 깊은 레이어로 갈수록 더 복잡하고 구체적인 특징을 학습한다. e.g., texture, 둥근 모양

결국에는 인식하고자 하는 다리, 꽃, 개별 물체와 구조를 학습한다. 링크

Cost Function : J(G)

C, S로 G를 만드는 문제다.
콘텐츠 유사성과 스타일 유사성을 평가하면 된다.
하이퍼파라미터 $\alpha, \beta$로 C, S의 가중치를 정한다.

$J(G) = \alpha J_{content}(C, G) + \beta J_{style}(S, G)$

• $J_{content}(C, G) = \frac{1}{2} ||a^{[l](C)} - a^{[l](G)}||^2$
• $J_{\text{style}}^{[l]}({S}, {G}) = \frac{1}{(2n_H^{[l]} n_W^{[l]} n_C^{[l]})^2} \sum_{k} \sum_{k'} \left( G_{kk'}^{[l]({S})} - G_{kk'}^{[l]({G})} \right)^2$
  • Style을 수치화하기 위해 서로다른 채널 $k, k'$ 사이의 correlation을 본다.
  • Style의 차이를 보기 위해 S의 채널간 correlation, G의 채널간 correlation을 비교한다.
  • (프로베니우스노름의 제곱)

학습할 때는 그냥 G를 무작위로 초기화하고, 경사하강법으로 G의 픽셀값을 업데이트하면 된다.
$G := G - \frac{\partial J(G)}{\partial G}$