타일 채우기
문제
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
입력
첫째 줄에 N(1 ≤ N ≤ 30)이 주어진다.
출력
첫째 줄에 경우의 수를 출력한다.
예제

풀이
- N이 홀수일 경우 항상 타일이 부족하다! => 짝수일때만 고려해야한다.
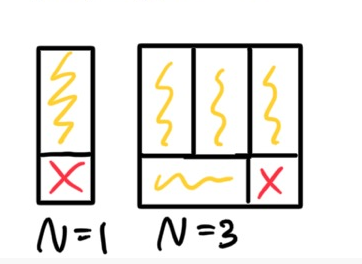
-
N = 2일 경우
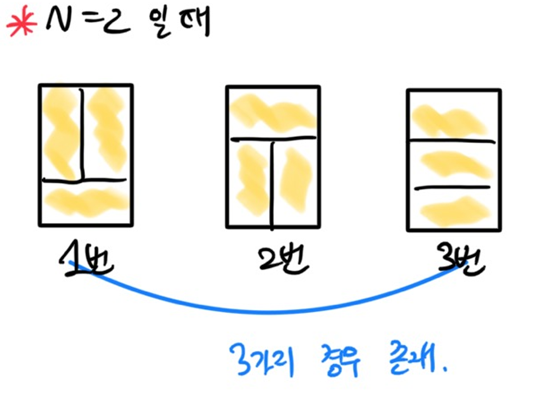
-
N = 4일 경우
- N = 2일 때
타일의 경우의 수가 3이므로
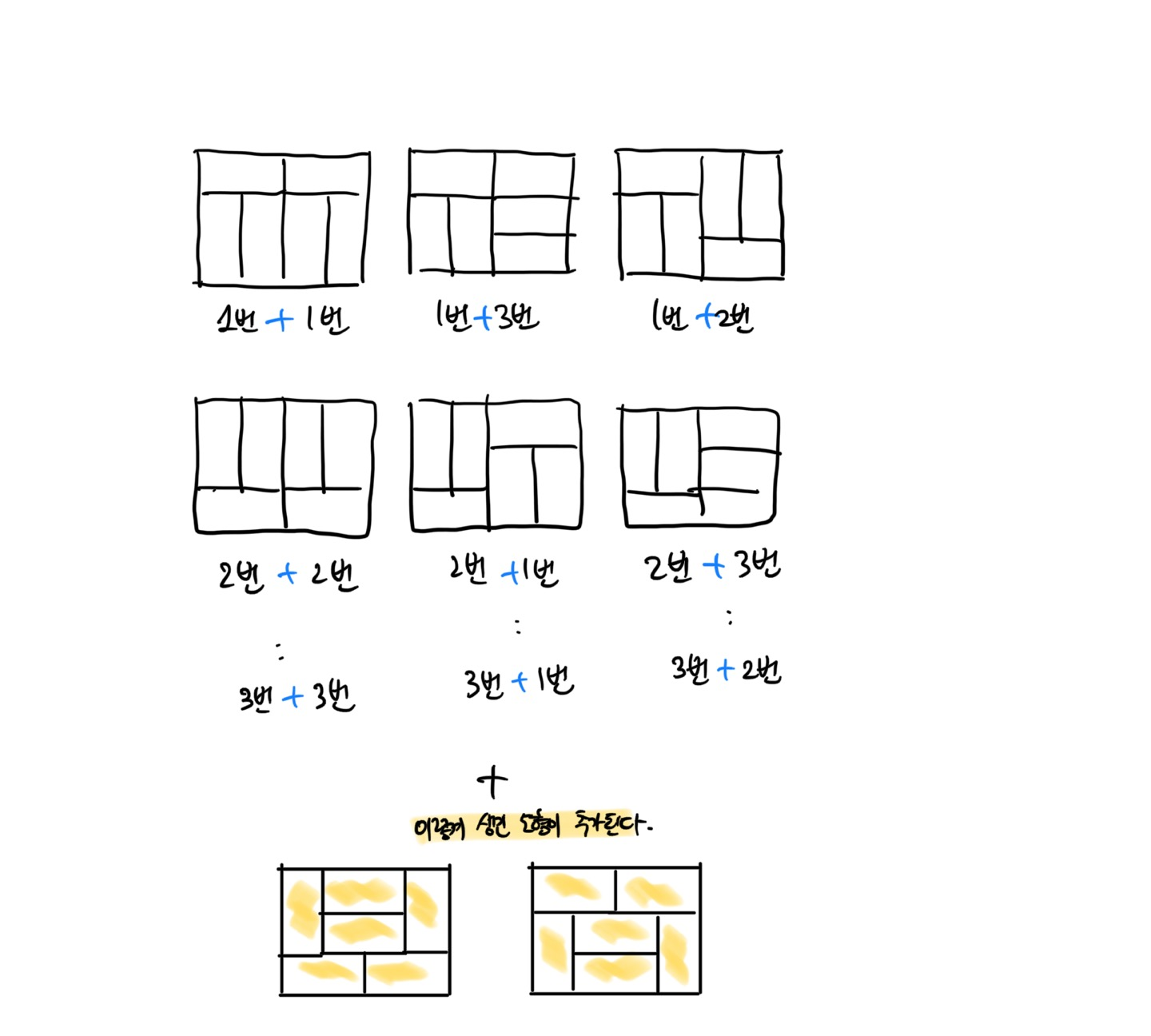
위 9개의 경우의 수와1번 + 1번, 1번 + 2번, 1번 + 3번 2번 + 1번, 2번 + 2번, 2번 + 3번 3번 + 1번, 3번 + 2번, 3번 + 3번
- N = 4일때 고유한(?) 모양의 타일 2개가 존재한다.
따라서 dp[4] = dp[2] * dp[2] + 2 = 11이다.
- N = 6일 경우
-
타일의 경우의 수를 나누어서 생각해줘야 한다.
.
3-1) (3 X 4)의 타일에 (3 X 2) 타일이 붙는 경우
3-2) (3 X 2) 의 타일에 (3 X 4) 타일이 붙는 경우
3-3) (3 X 6) 고유한 패턴의 타일 2개
. -
3-1)번의 경우는 당연히 3X4의 타일에 3X2의 타일이 붙는 경우이므로
3x4 타일의 경우의 수와 3x2 타일의 경우의 수를 곱해준 값이 답이다.
즉dp[6] = dp[4] * dp[2]가 될 것이다.
. -
3-2)번의 경우를 생각해보자
3-2)에 3-1)번과 같이 3x2의 경우와 3x4의 경우를 곱해주면 당연히중복이 발생한다! 3x4에는 3x2가 포함되어있기 때문이다. 아래의 그림을 보면 이해가 쉬울 것이다.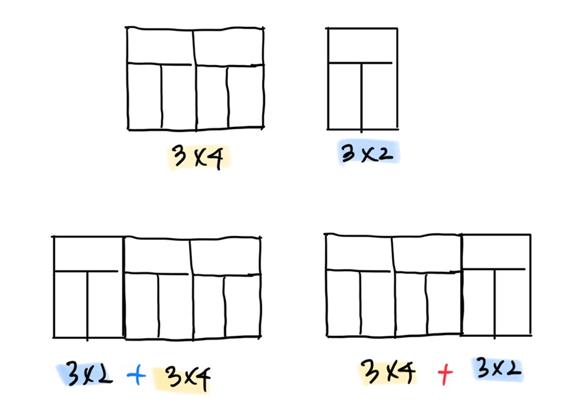
따라서 우리는 중복 없이 3x2타일과 3x4 타일이 붙는 경우를 고려해줘야 한다.
아직 세지 않은 경우의 수는 3x2 타일과 3x4 고유의 타일 2개가 붙는 경우이다.
우리는 3-1)번의 케이스에서 고유한 3x4 타일에 3x2 타일이 붙는 경우는 세어 주었다.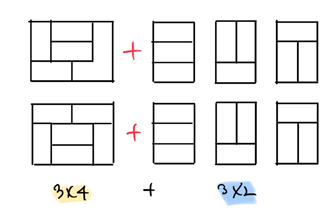
따라서 3x2 타일에 고유한 3x4 타일이 붙는 경우만 고려해주면 중복 없이 3x4와 3x2 타일이 붙는 경우를 모두 세어준 것이 된다!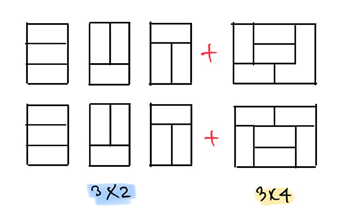 위 경우의 수는 3x2의 타일에 3x4 고유한 타일 두개가 붙는 경우이므로
위 경우의 수는 3x2의 타일에 3x4 고유한 타일 두개가 붙는 경우이므로
dp[2]*2가 된다. -
3-3) N = 6일 경우 고유한? 모양 2개도 더해줘야 한다.

-
모든 경우의 수를 조합해봤을 때
dp[6] = dp[4]*dp[2] + dp[2]*2 + 2 = 41이 된다.
- N=8
- N=8일 때에도 동일하게 타일의 경우의 수를 나누어서 생각해주면 된다.
.
4-1) (3 X 6)의 타일에 (3 X 2) 타일이 붙는 경우
4-2) (3 X 4) 의 타일에 (3 X 4) 타일이 붙는 경우 (3X4 고유한 타일 2개)
4-3) (3 X 2) 의 타일에 (3 X 6) 타일이 붙는 경우 (3X6 고유한 타일 2개)
. - 따라서 dp[8]은
dp[8] = dp[6] * dp[2] + dp[4] * 2 + dp[2] * 2 + 2의 식으로 표현할 수 있다.
점화식
위 규칙들로 아래의 점화식을 도출할 수 있다.
dp[0]은 1로 지정한다. (N이 4 이상일 경우, 항상 고유한 타일 2개가 나오는것을 고려)
dp[N] = dp[N-2]*dp[2] + dp[N-2-2]*2 + dp[N-2-2-2]*2 ... dp[0]*2 (단, N은 4보다 크다)
정답 코드
n = int(input())
dp = [0]*(n+1)
dp[0] = 1
if n >= 2:
dp[2] = 3
for i in range(4,n+1,2):
dp[i] = dp[i-2] *dp[2]
for j in range(0,i-2, 2):
dp[i] += dp[j]*2
print(dp[n])
느낀점?
- 런타임에러
n이 2보다 클 때를 고려 안해서 런타임 에러 났었다...
백준은 이래서 어렵다.. 예상치못한 예제의 경우가 많다 ㅠ !
수정 전에 dp[0] = 1, dp[2] = 3
이렇게 값을 할당했었는데, N=1인 경우 위 코드에서 인덱스 오류가 났다.
(dp[2]가 존재하지 않았음! )
다른사람들의 경우 dp = [0]*31 (문제에서 주어진 n의 최대값) 이런식으로도 풀던데 이 방식도 고려해보자!
