[python/백준/DP] 2011: 암호코드

문제

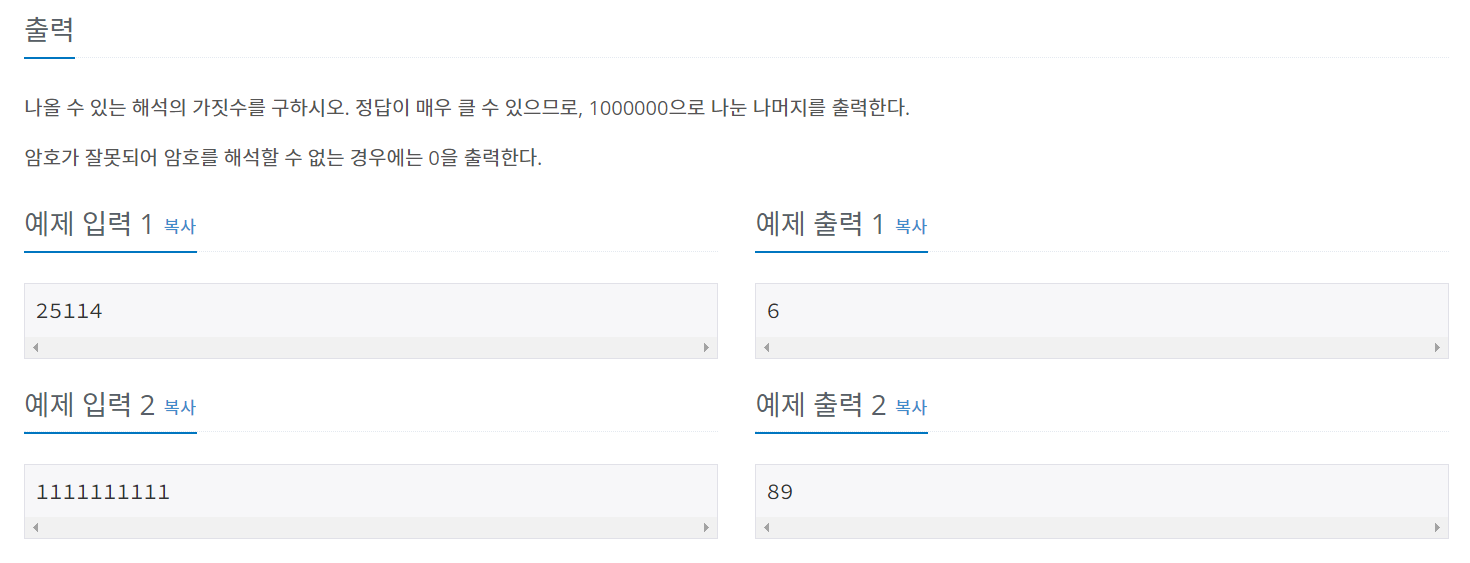
풀이

[a] : 숫자가 따로 존재하는 경우
[b] : 숫자가 결합해서 존재하는 경우

case 1. 암호 : 25114

  dp[n] = 암호 n의 자리수 까지 가능한 경우의 수 

  dp[1] = 1가지 (2)
  dp[2] = 2가지 (2,5 / 25)
  dp[3] = 3가지 (2,5,1/ 25,1)
  dp[4] = 4가지 (2,5,1,1/ 25,1,1/ 2,5,11/ 25,11)
  dp[5] = 6가지 (2,5,1,1,4/ 25,1,1,4/ 2,5,11,4/ 25,11,4/ 2,5,1,14/ 25,1,14/ )

          [a]          [b]
  dp[2] = 1 +     dp[1] (단, n[1]*10 + n[2] < 27)
  dp[3] = dp[2] + dp[1] (단, n[2]*10 + n[3] < 27)
  dp[4] = dp[3] + dp[2] (단, n[3]*10 + n[4] < 27)
  dp[5] = dp[4] + dp[3] (단, n[4]*10 + n[5] < 27)


case 2. 암호 : 20401

  dp[n] = 암호 n의 자리수 까지 가능한 경우의 수 

  dp[1] = 1가지 (2)
  dp[2] = 1가지 (20)
  dp[3] = 1가지 (20,4)
  dp[4] = 0가지 (20,40) ---> 불가 

          [a]                  [b]
  dp[2] = 0 (2,0 불가능) + dp[1] (20 가능) = 1

          [a]                  [b]
  dp[3] = dp[2]       +        dp[1]
          1 (20,4 가능) + (2,04 불가능)

          [a]                   [b]
  dp[4] = dp[3]       +        dp[2] 
          0 (20,4,0 불가능)  +  (20,40 불가능)  
        

따라서, 

  dp[n-1]을 고려할 때 (숫자가 따로 존재하는 경우)
          1) 암호[n]이 0이면 dp[n] = 0 
          2) 암호[n]이 0보다 크면 dp[n] = dp[n-1]

  dp[n-2]를 고려할 때 (숫자가 결합해서 존재하는 경우)
          1) 암호[n-1]이 0이면 dp[n] += 0
          2) 암호[n-1]*10 + 암호[n] < 27이면
              dp[n] += d[n-2]    


만약 두 결과를 합쳐서 나온 값이 0이라면 
암호 해독이 불가능한 경우이다! 

위 알고리즘으로 문제를 풀어보자 

코드

n = input()
dp = [0 for _ in range(len(n)+1)]

# 암호가 0으로 시작한다면 아예 해독이 불가능하다 
if n[0] == '0':
    print('0')

# 암호가 0으로 시작하지 않는 경우      
else:    
    # dp[0], dp[1] 은 항상 1이다. 
    # dp[0]은 dp[2]를 처리하기 위해 1로 지정해준다. 
    dp[0] = 1 
    dp[1] = 1
    
    # dp의 index와 n의 index를 맞추기 위해 0을 추가해준다. 
    n = '0'+n
    for i in range(2,len(n)):
        # case [a] : i번째 숫자가 단독으로 존재하는 경우 
        if n[i] > '0':
            dp[i] += dp[i-1]
        # case [b] : i번째 숫자가 결합해서 존재하는 경우
        if n[i-1] != '0' and n[i-1] + n[i] < '27':
            dp[i] += dp[i-2]

    print(dp[len(n)-1]%1000000)

✨ 후기

다 풀었다 생각했는데 해석이 불가능한 암호를 생각하지 못했다.
0이 있는 경우를 생각하지 못해서 엄청 틀렸다 ㅠㅠ 노력의 흔적..^..^..
백준... 예시 좀만 더 줘 ㅠㅠ